Добавил:

turbo1121 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Петербургский государственный университет путей сообщения им. императора Александра I

Предмет:

Теоретическая механика

Файл:

1350

.pdf

Скачиваний:

Добавлен:

23.12.2017

Размер:

1.24 Mб

Скачать

☆

1 / 71 2 3 4 5 6 7 > Следующая >>>

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НИЗКОТЕМПЕРАТУРНЫХ И ПИЩЕВЫХ ТЕХНОЛОГИЙ

Кафедра теоретической механики

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА ДИНАМИКА

Методические указания к практической и самостоятельной работе

студентов всех специальностей очной и заочной форм обучения

Санкт-Петербург

2009

УДК 531(075)

Григорьев А.Ю. Теоретическая механика. Динамика: Метод. указания к практической и самостоятельной работе студентов всех спец. очной и заочной форм обучения. – СПб.: СПбГУНиПТ, 2009. – 68 с.

Представлен теоретический материал, приведены примеры решения задач, а также даны задачи для самостоятельной работы студентов по соответствующим темам дисциплины «Динамика».

Рецензент Доктор техн. наук, проф. В.А. Арет

Рекомендованы к изданию редакционно-издательским советом уни-верситета

Санкт-Петербургский государственный университет низкотемпературных и пищевых технологий, 2009

Часть I. ТЕОРИЯ, НЕОБХОДИМАЯ ДЛЯ РЕШЕНИЯ ЗАДАЧ ДИНАМИКИ

Динамика – это раздел теоретической механики, в котором изучается движение материальных тел под действием приложенных к ним сил.

Покой – частный случай движения, поэтому раздел статики – это частный случай динамики.

Кинематика исследует движение материальных тел с чисто геометрической точки зрения, следовательно, кинематику можно считать геометрическим введением в динамику.

Динамика делится на динамику материальной точки и на динамику системы материальных точек.

1. Динамика материальной точки

Аксиомы динамики (законы динамики)

1.Материальная точка, на которую не действуют внешние силы, находится в покое или движется равномерно и прямолинейно. Иначе: изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного и прямолинейного движения.

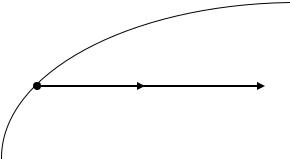
2.Действующая на материальную точку сила вызывает пропорциональное ей ускорение (рис. 1).

Эту аксиому можно записать формулой

(1)

где F – вектор силы; W – вектор ускорения движения материальной

точки; m – коэффициент пропор-

циональности, называемый инер-

ционной массой точки.

Инерционная масса m опре-

деляет способность тела сопро-

тивляться изменению характера

движения. Соотношение (1), уста-

навливающее связь между силой

Рис. 1

F , массой m и ускорением W ,

является важнейшим в классической механике и называется основ-

ным уравнением динамики материальной точки. (1-я форма).

Пример: Материальная точка свободно падает вблизи поверхности планеты Земля (рис. 2). Согласно все- m мирному закону тяготения, сила притяжения двух тел друг к другу определяется формулой

m M

F G

(2)

где

m – масса материальной точки; М – масса

планеты Земля; R – расстояние между мате-

риальной точкой и центром планеты; G –

Рис. 2

универсальная гравитационная постоянная.

Но, согласно основному закону динамики,

, следова-

тельно, ускорение свободного падения

g W

(3)

Отсюда видим, что ускорение свободного падения g не зависит от массы падающего тела.

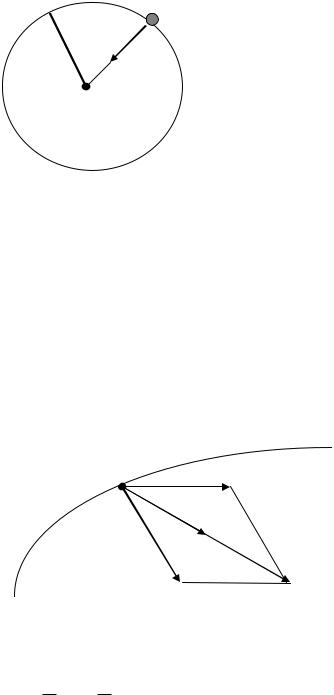
где F F i

i 1

3. Несколько

одновре-

менно действующих на мате-

риальную точку сил (рис. 3)

сообщают точке такое ускоре-

F 1

ние, какое сообщила бы ей од-

на сила, равная их геометри-

ческой сумме, т. е. если на ма-

териальную

точку

действует

F 2

система сил

F 1 , F 2

,... F n ,

то

Рис. 3

mW F i ,

(4)

i 1

– равнодействующая системы сил.

Пример: на материальную точку М действуют две силы F1

и F 2 , в этом случае вектор W ускорения ее движения будет направ-

лен по диагонали параллелограмма со сторонами F1 и F 2 туда же, куда действует равнодействующая сила F .

4. Движущиеся материальные точки взаимодействуют друг с другом с силами, равными по модулю и действующими вдоль одной прямой в противоположные стороны.

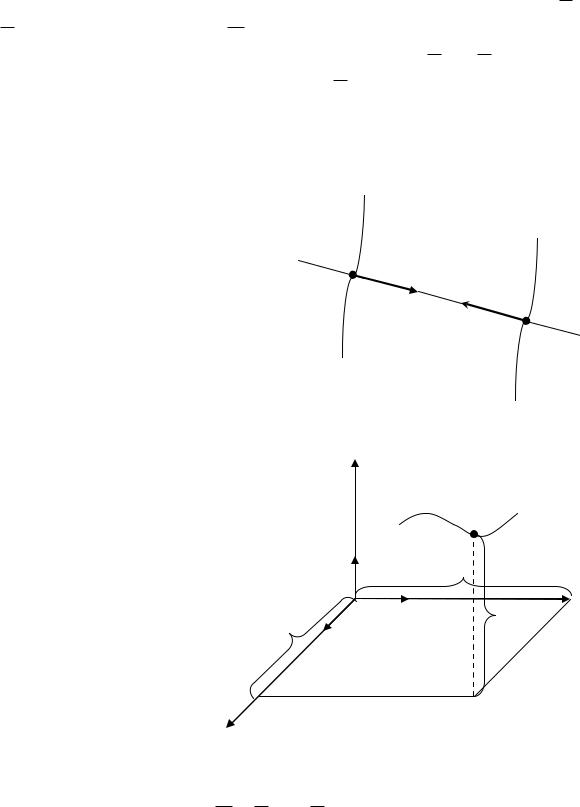
Так, например (рис. 4), F1 = − F 2 .

Аксиомы

динамики были

впервые сформулированы англий-

ским ученым Исааком Ньютоном

F 1

применительно

инерциальным

F 2

системам отсчета,

т. е. к системам

отсчета, покоящимся или движущимся равномерно и прямолинейно.

Рис. 4

Дифференциальные уравнения движения материальной точки

Пусть

материальная

M x, y, z

точка М массой m (рис. 5)

движется

под

действием

произвольной системы сил

F 1 , F 2 ,... F n ,

равнодейст-

вующая которой F F i .

i 1

Тогда основной закон ди-

намики для этой точки вы-

глядит следующим обра-

зом:

Рис. 5

n
m W F F i .	(5)

i 1

Введем в пространстве произвольную декартову систему координат Oxyz с ортами осей i, j, k . Тогда координаты положения точки М являются функциями времени (см. раздел кинематики, ко-

ординатный способ задания движения материальной точки), следо-

вательно:

x x(t)
y y(t) ,	(6)
z z(t)

где х, у, z – переменные координаты точки М, зависящие от времени. Из кинематики мы знаем, что вектор ускорения материальной точки W при координатном способе задания движения определяется

выражением

(7)

где

d 2 x

, y

d 2 y

, z

d 2 z

dt2

Вектор силы Fi

через свои проекции на оси координат запи-

шется в следующем виде:

i Xi

k ,

(8)

где

Xi , Yi ,

Z i – проекции вектора силы Fi

на оси

координат

Оx, Оy, Оz соответственно, а вектор равнодействующей силы через свои проекции запишется в виде

			Y		Z		.	(9)
F	X	i		j		k

Вспоминая теорему о проекции геометрической суммы на ось, получаем, что

n	n	n
X Xi ,	Y Yi ,	Z Zi .	(10)
i 1	i 1	i 1

Спроектируем векторное основное уравнение динамики материальной точки (5) на оси координат с учетом выражений (7)–(10), получим дифференциальные уравнения движения материальной точки

	n
mx X X i
	i 1	(11)
	n	(11)
	n
my Y Yi
	i 1
	n

mz Z Zi
	i 1

Система дифференциальных уравнений (11) – это вторая форма записи основного уравнения динамики материальной точки.

Две задачи динамики

Различают две задачи динамики – прямую и обратную.

Первая прямая задача динамики состоит в определении рав-

нодействующей силы, действующей на точку известной массы, движущейся по заданному закону.

Пример: пусть известен закон движения материальной точки

ион задан координатным способом:

xx(t) , y y(t) , z z(t) .

Тогда, согласно выражению (11), декартовы проекции на оси координат равнодействующей силы можно определить по формулам

X mx , Y my , Z mz .

А далее равнодействующая сила находится по формуле (9).

Таким образом, первая задача динамики может быть решена всегда с помощью операции двойного дифференцирования по времени выражений для закона движения материальной точки.

Пример: пусть материальная точка движется в плоскости Oxy по закону

x a coskt ,

у b sin kt ,

где a, b, k const.

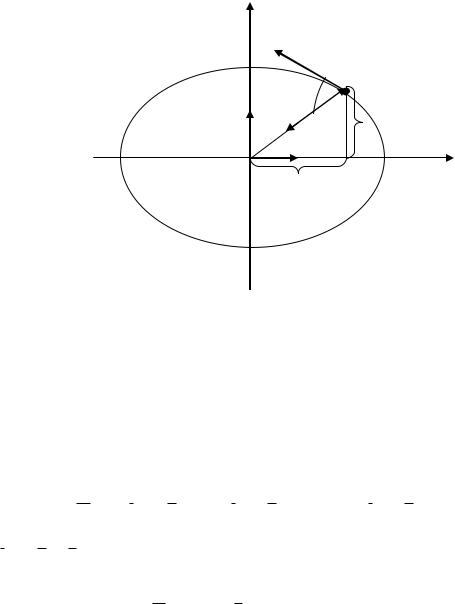
Тогда очевидно, что траектория движения описывается уравнением

т. е. траекторией движения материальной

точки

является эллипс

с полуосями a и b . Из условия задачи (рис. 6) имеем:

i x

Рис. 6

x ak sin kt , y bk coskt ,

x ak2 coskt k 2 x ,y bk2 sin kt k 2 y .

Так как X mx , Y my , то

F X i Y j m x i y j mk 2 xi y j ,

где xi y j r – радиус-вектор положения материальной точки М в пространстве.

Следовательно, F mk 2 r .

Таким образом, данное движение происходит под действием силы, всегда направленной к центру эллипса (см. рис. 6). Модуль этой

силы пропорционален расстоянию до центра эллипса: F mk 2OM .

Вторая обратная задача динамики состоит в определении закона движения материальной точки известной массы по заданным силам.

Так, пусть действующие на материальную точку силы заданы как функции:

1)времени t;

2)координат положения материальных точек x, y, z ,

3)компонент (составляющих) вектора скорости x, y, z ,

где новые обозначения производных по времени x, y, z									соответству-
ют x	dx	, y	dy	,	z	dz	.
ют x		, y		,	z		.
	dt		dt			dt
Тогда дифференциальные уравнения движения материальной
точки (11)		запишутся в виде
					mx X x, y, z, x, y, z, t
					my Y x, y, z, x, y			, z, t	(12)

					mz Z x, y, z, x, y			, z, t ,

откуда видим, что получена система трех дифференциальных уравнений шестого порядка относительно трех неизвестных x, y, z .

Для определения закона движения в координатной форме необходимо проинтегрировать эту систему уравнений. В процессе интегрирования возникнут шесть произвольных констант интегрирования. Чтобы определить эти постоянные, следует задать начальные усло-

вия. Начальные условия определяют положение и скорость			точки
в момент начала движения t0 = 0.
При t = t0, х = х0,	у = у0,	z = z0;
x x0 ,	y y0 ,	z z0 ,	(13)

где x0 , y0 , z0 – известные координаты начального положения материальной точки в пространстве; x0 , y0 , z0 – известные компоненты (составляющие) вектора начальной скорости движения материальной точки.

Следовательно, для решения задачи, кроме системы уравнений (12), необходимо иметь шесть начальных условий (13).

2. Теоремы об изменении импульса (количества движения)

Понятие о количестве движения материальной точки (импульс материальной точки)

Пусть некоторая материальная точка массы m движется по

криволинейной траектории со скоростью .

Определение: Количеством движения материальной точки называется векторная величина, равная произведению массы точки на

вектор скорости:
Q m .	(1)

Очевидно, размерность количества движения в системе СИ:

Q кг мс Н с; в СГСЕ: Q кгс.

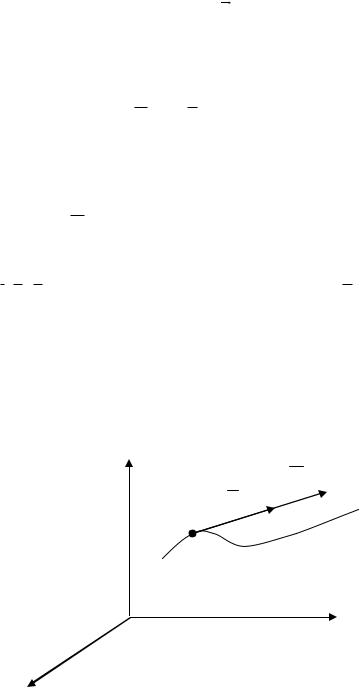
Введем прямоугольную декартову систему координат Oxyz с ортами осей i, j, k (рис. 7), тогда вектор скорости через свои проекции на оси координат можно записать в следующем виде (см.

раздел кинематики, координатный способ задания движения материальной точки):

				y		z		.
		x	i	y	j	z	k	.	(2)

Рис. 7

1 / 71 2 3 4 5 6 7 > Следующая >>>

Соседние файлы в предмете Теоретическая механика

#
23.12.20171.24 Mб991350.pdf
#
23.12.2017197.62 Кб17g1Y7yACOnPE.jpg
#
20.12.20174.37 Mб219Кинематика Ответы.docx
#
20.12.20174.75 Mб315Статика Ответы.docx