
Задачник / Глава 06 (112-155)
.pdf
Глава 6 Плоский изгиб стержней
6.1 Теоретическая и методическая информация.
Примеры
6.1.1 Внутренние усилия при плоском поперечном изгибе стержней с прямолинейной осью
Для определения внутренних усилий при плоском изгибе применяется метод сечений. Любая отсеченная часть балки должна находиться в равновесии под действием внешних сил и внутренних усилий в сечении.
При плоском изгибе в поперечных сечениях балок возникают два внутренних усилия – изгибающий момент Мx и поперечная сила Qy .
Изгибающий момент равен алгебраической сумме моментов всех внешних сил, действующих с одной стороны от сечения, относительно нейтральной оси x, проходящей через центр тяжести проведенного сечения.
Поперечная сила равна алгебраической сумме проекций на нормаль к продольной оси стержня всех внешних сил, приложенных с одной стороны от сечения.
Правило знаков для внутренних усилий М и Q в соответствии с ранее сформулированным правилом (п. 1.1.7), применительно к плоскому изгибу балок для двух вариантов координатных осей показано на рисунке 6.1.
z z
M>0 |
|
|
Q>0 |
|
|
M>0 |
|
|
Q>0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
y |
Рис. 6.1
В процессе построения эпюр М и Q, а также при проверке конечных результатов рекомендуется пользоваться следующими правилами.
1. Ординаты эпюры М откладываются перпендикулярно оси эпюры со стороны растянутых волокон балки. Положительные значения М и Q откладываются в соответствии с положительным направлением оси у снизу от оси, отрицательные – сверху.
2. На эпюре М должны наблюдаться скачки в сечениях балки, где приложены внешние сосредоточенные моменты. Величина скачка должна быть равна моменту.
112
3.В эпюре Q скачки должны наблюдаться в сечениях, где приложены сосредоточенные силы (активные и реактивные). Величина скачка равна сосредоточенной силе.
4.На участках без распределенной нагрузки эпюра М очерчена на-
клонной прямой при Q 0 и горизонтальной прямой (в частности может быть и с нулевой ординатой) при Q=0; эпюра Q на участках без распределенной нагрузки очерчена горизонтальной прямой (в частности может быть с нулевой ординатой).
5.В пределах участка балки, где действует равномерно распределенная нагрузка, эпюра М имеет параболическое очертание, эпюра Q – наклонная прямая.
6.В тех сечениях балки, где поперечная сила переходит через нуль, изгибающий момент имеет экстремальное значение (max или min), т. к.
Q dM . |
|
dz |
|
7. Эпюра М имеет переломы в местах приложения сосредоточенных |
|
сил. Эпюра Q имеет переломы в местах изменения интенсивности распре- |
|
деленной нагрузки. |
|
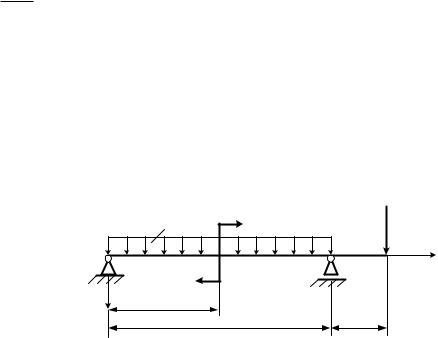
Пример 6.1.1. Схема балки представлена на |
рисунке 6.2. |
Дано: F = 20 кН; q = 10 кН/м; m = 30 кНм; l = 4 м; |
а = 1 м. |
Построить эпюры М и Q .
|
|
m |
F |
|
q |
|
|
|
|
|
|
A |
|
|
B |
|
|
z |
|
|
|
|
|
y |
l/2 |
|
а |
|
|
l |
Рис. 6.2
Решение. 1. Определение опорных реакций (рис. 6.3).
1) М B 0 ; |
VAl |
ql 2 |
m Fa 0 ; |
||||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
V |
|
|
Fa |
m |
|
ql |
; V |
|
|
|
20 1 |
|
|
30 |
|
10 4 |
7,5 кН; |
||||
A |
|
|
A |
|
|
|
|||||||||||||||
|
|
l |
l |
2 |
|
|
|
|
|
4 |
|
4 |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2) М А 0 ; |
RBl |
ql 2 |
|
m F(a l) 0; |
|||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
113

R |
ql |
m |
|
F (a l) |
; |
R |
10 4 |
|
30 |
|
20 5 |
52,5 кН; |
||
|
|
|
|
|
||||||||||
B |
2 |
l |
|
l |
|
|
B |
2 |
4 |
4 |
|
|||
|
|
|
|
|
|
|||||||||
3) Z 0; |
H A 0. |
|
|
|
|
|
|
|
|
|
|
|||
Проверка: Y 0; |
VA VB ql F 0; |
|
|
|
||||||||||
7,5 52,5 10 4 20 0; |
|
0 0. |
|
|
|
|
|
|||||||
2. Построение эпюр Q и M.
В пределах длины балки три участка: I – от VA до m , II – от m
до RB , III – от RB |
до F. Проводим сечение в границах первого участка. |
|||||||
I участок: |
0 z1 l / 2 . |
|
|
|
||||
|
Q1 VA qz1 7,5 10z1; |
|
||||||
|
M |
|
V |
z |
qz12 |
7,5z 5z2 . |
||
|
1 |
|
||||||
|
|
|
A 1 |
2 |
1 |
1 |
||
|
|
|
|
|
|
|
|
|
Функция Q1 – линейная, поэтому для построения ее эпюры достаточно определить два значения поперечной силы в начале и конце участка. Функция М1 – нелинейная (параболическая). Для построения эпюры М1 в таком случае необходимо располагать по крайней мере тремя значениями изгибающего момента. Два из них берутся на границах участка, третье – в том сечении, где функция М1 достигает экстремума. Если в пределах участка нет экстремума, то определяется промежуточное значение момента в
середине участка. Известна зависимость dMdz Q , следовательно, там, где
поперечная сила становится равной нулю, момент достигает экстремума (по правилам отыскания экстремума функции). Таким образом, о наличии экстремума на эпюре моментов в пределах данного участка можно судить
по признаку – переходит ли эпюра Q через ноль.
Если поперечная сила меняет знак с плюса на минус, то имеет место максимум момента (как в данном случае), а если поперечная сила переходит через ноль, меняя знак с минуса на плюс, то момент в точке экстремума достигает минимума.
Итак, приравняем нулю Q1 или производную функции М1 и найдем z1* , соответствующее M max :
Q |
dM1 |
0; V |
A |
qz* 0; |
z* |
VA |
|
7,5 |
|
0,75 м. |
|
|
|
||||||||
1 |
dz1 |
|
1 |
1 |
q 10 |
|
||||
|
|
|
|
|
|
|||||
Подсчеты Q и М для построения эпюр сведены в таблицу 6.1.
II участок: l / 2 z2 l . Рассматриваем часть балки слева от сече-
ния:
114

Q2 |
|
VA qz2 7,5 10z2 ; |
|
|
|
|||||
M |
|
V |
z |
|
|
qz22 |
m 7,5z |
|
5z2 |
30 . |
2 |
2 |
|
2 |
|||||||
|
A |
|
2 |
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
||
Функция Q2 – линейная. Для построения эпюры Q2 достаточно определить два значения функции. Функция М2 – нелинейная. Для построения ее эпюры надо знать не менее трех значений функции М2. Подсчеты приведены в таблице 6.1. Так как в пределах второго участка Q2 не переходит через ноль, то функция М2 не имеет экстремума в пределах участка
иподсчитывается М2 при z2= 3 м.
III участок: l z3 l a . Рассматриваем равновесие правой отсе-
ченной части:
Q3 F 20 кН;
M3 F(l a z3 ) 20(5 z3 ).
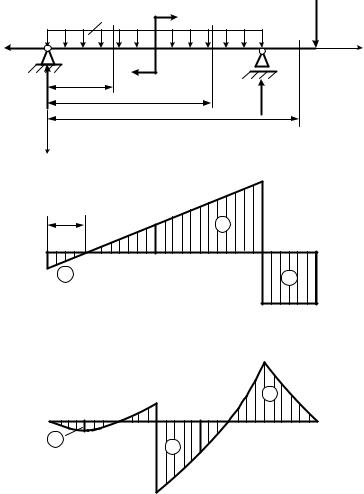
По данным таблицы 6.1 построены эпюры Q и М (рис. 6.3).
|
|
|
Т а б л и ц а 6 . 1 |
|
|
|
|
|
|
Участок |
z, м |
Q, кН |
|
М, кНм |
|
|
|
|
|
|
0 |
7,5 |
|
0 |
|
|
|
|
|
I |
0,75 |
0 |
|
2,81 |
|
|
|
|
|
|
2 |
–12,5 |
|
–5 |
|
|
|
|
|
|
2 |
–12,5 |
|
25 |
|
|
|
|
|
II |
3 |
–22,5 |
|
7,5 |
|
|
|
|
|
|
4 |
–32,5 |
|
–20 |
|
|
|
|
|
III |
4 |
20 |
|
–20 |
|
|
|
|
|
5 |
20 |
|
0 |
|
|
|
|||
|
|
|
|
|
Примечание. Для консольных балок с одним защемленным и другим свободным концами определение опорных реакций не является обязательным. При построении эпюр Q и М в них следует рассматривать равновесие отсеченного свободного конца балки.
115
|
|
|
m |
|
F |
|
|
q |
|
|
|
|
|
|
|
|
|
HA |
|
|
|
B |
|
|
z1 |
|
|
|
z |
VA |
z2 |
|
|
|
|
|
|
R |
B |
||
|
|
|
|
z3 |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
Эп. Q, кН |
32,5 |
|
|
z |
12,5 |
- |
|
|
|
|
|
|
|||
|
|
|
|
|
|
7,5 |
+ |
|
|
+ |
|
|
|
|
|
20 |
20 |
|
|
Эп. М, кНм |
20 |
|
|
|
|
5 |
|
- |
|
|
|
|
|
|
|
+ |
2,81 |
|
+ |
|
|
|
|
|
7,5 |
|
|
|
|
25 |
|
|
|
|
|
|
Рис. 6.3 |
|
|
6.1.2 Эпюры внутренних усилий при плоской деформации рам
При плоском изгибе в поперечных сечениях рамы возникают три внутренних усилия – М, Q, N. Осью эпюр М, Q, N служит ось рамы. Правило знаков для усилий при этом можно оставить таким же, как оно было сформулировано ранее.
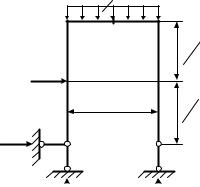
Пример 6.1.2. Дано: h = 4 м; l = 3 м; F = 30 кН; q = 20 кН/м (рис. 6.4).
Построить эпюры М, Q, N.
116
|
|
q |
|
|
|
C |
h 2 |
|
F |
|
|
|
|
|
|
|
|
l |
h 2 |
HА |
А |
|
|
|
B |
VA |
|
RB |
Рис. 6.4
Решение. 1. Определение опорных реакций.M A 0;
|
|
|
|
R l |
ql 2 |
F |
h |
0; |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
B |
|
|
|
2 |
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
R |
ql 2 |
Fh |
|
20 9 30 4 |
50 кН; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
B |
|
|
2l |
|
|
|
|
|
|
2 3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
M B 0; |
|
|
|
|
|||||||||
|
|
|
V |
|
l F |
h |
|
|
ql 2 |
|
0; |
|
|
||||||
|
|
|
A |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
V |
|
Fh ql2 |
|
30 4 20 9 |
10 кН; |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A |
|
|
2l |
|
|
|
|
|
|
|
2 3 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
X 0; H A F 0; H A F 30кН.
Проверка. Для проверки составим сумму моментов относительно середины ригеля (точка С, рис. 6.4):
M |
|
0; |
V |
|
l |
H |
|
h F |
h |
R |
l |
0; |
|
A 2 |
|
|
|
||||||||
|
C |
|
|
|
A |
2 |
B 2 |
|
||||
10 1,5 ( 30) 4 30 2 50 1,5 0; |
|
0 0. |
||||||||||
2.Число участков на раме равно четырем.
3.Определение внутренних усилий и построение эпюр.
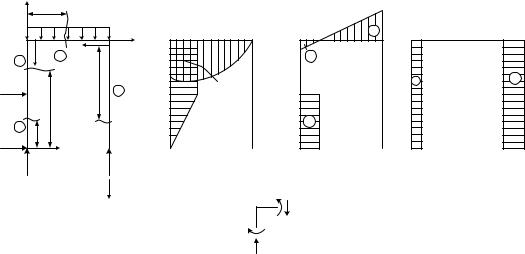
Для определения внутренних усилий введем подвижную систему координат zy. Начало координат будем размещать в начале каждого прямолинейного участка рамы, обходя ее по ходу часовой стрелки от левой опоры. Ось y направим внутрь рамы, ось z – вдоль оси соответствующего прямолинейного элемента (рис. 6.5, а).
117
а) |
z |
z3 |
|
|
|
б) |
|
в) |
50 |
г) |
|
|
|
|
|
|
|
|
|
||||
|
Г |
|
|
|
z |
|
60 |
|
- |
10 |
50 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
2 |
y |
3 |
y |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z4 |
|
60 |
62,5 |
|
|
- |
- |
F |
|
|
4 |
|
|
30 |
|||||
|
|
|
|
60 |
|
|
|
||||
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
z1 |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
HA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
y |
|
|
|
|
|
10 |
50 |
|
|
VA |
|
|
|
RB |
|
Эп. М, кНм |
|
Эп. Q, кН |
|
Эп. N, кН |
|
|
|
|
|
z |
|
д) |
60 кНм |
|
|
|
|
|
|
|
|
|
|
Г |
10 кН |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
60 |
|
|
|
|
10
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.5 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
I участок: |
|
0 z |
|
|
h |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
M1 H A z1; |
|
|
Q1 H A ; |
|
N1 VA . |
||||||||||||||||||||||||
Функции N1 |
и Q1 – постоянны, M1 – линейная. |
|
|
|||||||||||||||||||||||||||
II участок: |
|
h |
z |
|
h . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
M 2 H A z2 F z2 |
|
|
|
; Q2 |
H A F; |
N2 VA . |
||||||||||||||||||||||||
2 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Функции N2 |
и Q2 – постоянны, M2 – линейная. |
|
|
|||||||||||||||||||||||||||
III участок. Рассмотрим равновесие левой отсеченной части рамы. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 z3 l ; |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
M |
|
H |
|
h F |
h |
V |
|
z |
|
|
qz32 |
; |
|
|
||||||||||||
|
|
|
|
3 |
A |
|
A |
3 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Q3 VA qz3; N3 |
H A F . |
|
|
|||||||||||||||||||||||
Функции N3 |
– постоянна, Q3 |
– линейно изменяется, M3 – парабола. |
||||||||||||||||||||||||||||
Подсчеты по всем участкам сведены в таблицу 6.2. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 6.2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Участок |
|
|
|
z, м |
|
|
|
|
|
Q, кН |
|
|
М, кНм |
|
|
|
N, кН |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
0 |
|
|
|
|
–10 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
30 |
|
|
|
|
|
60 |
|
|
|
|
–10 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
II |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
60 |
|
|
|
|
–10 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
60 |
|
|
|
|
–10 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
60 |
|
|
|
|
0 |
|
||
|
III |
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
62,5 |
|
|
|
|
0 |
|
||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
–50 |
|
|
|
|
|
0 |
|
|
|
|
0 |
|
||
|
IV |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
–50 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
–50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
118

Так как Q3 в пределах участка меняется от 10 кН до –50 кН, найдем z3, соответствующее значению Q3 = 0, следовательно, M3 экстр при
z3* VqA 1020 0,5 м.
IV участок. Внутренние усилия определим, рассмотрев равновесие нижней части правой стойки рамы (рис. 6.5, а):
0 z4 h ;
M 4 0; Q4 0; N4 RB 50 кН.
В соответствии с результатами выполненных расчетов (табл. 6.2) строим эпюры М, Q, N (рис. 6.5, б, в, г). Положительные ординаты отложим внутрь рамы, отрицательные – наружу. При этом эпюра моментов окажется построенной на растянутых волокнах.
Статическая проверка правильности построения эпюр в раме.
Каждый «вырезанный» из рамы узел должен находиться в равновесии под действием внешних сил, приложенных к узлу, и внутренних усилий в рассеченных стержнях.
Вырежем, например, узел Г (рис. 6.5, а, д). Направление внутренних усилий показываем в соответствии с эпюрами М, Q, N и правилами знаков для них. Составим уравнения равновесия для узла:
Y 0; N Q 10 10 0; Z 0; 0 0;
MГ 0; М М 60 60 0.
Легко убедиться в том, что каждый из оставшихся узлов рамы тоже находится в равновесии.
6.1.3Формулы для напряжений, проверки прочности
иопределения перемещений при плоском изгибе стержней
Нормальные напряжения при плоском изгибе в точке поперечного сечения с координатой y от нейтральной оси
Мy ,
I x
здесь I x – момент инерции сечения относительно нейтральной оси. Условие прочности при чистом изгибе:
|
|
|
max |
|
|
M max ymax |
; |
Wx |
|
|
I x |
|
|
; |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
I x |
|
|
ymax |
|
|
||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
119

M max .
max Wx
Если материал балки по-разному сопротивляется растяжению и сжатию и имеет разные допускаемые напряжения при растяжении [ p ] и при
сжатии [ сж ], а сечение не симметрично относительно нейтральной оси, то
|
|
|
|
M max |
|
|
|
|
|
|
|
|
|
|
|
M max |
|
|
|
|
|
. |
|
max |
|
|
|
|
|
|
p |
; |
|
min |
|
|
|
|
|
|
|
сж |
|||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Wxp |
|
|
|
|
|
|
Wxсж |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Здесь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wxp |
I x |
|
; |
|
Wx сж |
|
I x |
, |
|
|
|
|||||||
|
|
|
|
|
|
|
|
ymax сж |
|
|
|
|||||||||||
|
|
|
|
|
|
|
ymax p |
|
|
|
|
|
|
|
|
|
|
|||||
ymax p , ymax сж – расстояние от нейтральной оси до наиболее удаленных во-
локон в сечении в растянутой и сжатой зонах. Формула Д. И. Журавского:
|
Q |
S |
отс |
|
, |
|
|
|
|
||
I xby |
|
||||
|
|
|
|||
где Sотс – статический момент относительно нейтральной оси части площади поперечного сечения, расположенной выше или ниже точки, в которой подсчитывается касательное напряжение ;
by – ширина сечения на высоте, где определяется напряжение . |
|||||||||||
Определение главных напряжений при плоском изгибе: |
|||||||||||
|
|
|
1 |
|
|
; tg2 |
|
|
2 |
. |
|
|
гл |
|
2 4 2 |
гл |
|||||||
|
|
||||||||||
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
Расчетные (эквивалентные) напряжения для полной проверки прочности балок при плоском поперечном изгибе по четырем теориям прочности:
рI 12 
 2 4 2 ;
2 4 2 ;
рII 0,35 0,65
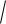 2 4 2 ;
2 4 2 ;
рIII 
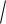 2 4 2 ;
2 4 2 ;
рIV 
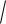 2 3 2 .
2 3 2 .
120
Дифференциальные зависимости между функциями прогибов , углов поворота сечения , изгибающего момента M , поперечной силы Q , распределенной нагрузки q , изменяющимися по длине стержня, при EI =
const представляются так: |
|
|
|
|
|
|
|
|||
|
M |
|
Q ; |
|
q ; |
M |
|
q ; |
|
|
|
|
Q |
|
|
||||||
z ; |
; |
M EI ; |
Q EI ; |
q EI IV , |
||||||
здесь штрихи обозначают производные по z.
Формула метода начальных параметров для определения перемещений при изгибе:
|
|
|
|
|
|
0 0 z |
|
M z 2 |
|
Q z |
3 |
|
|
q z4 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2EI |
|
|
6EI |
|
24EI |
|
|
|
|
|
||||||
n |
|
|
|
|
|
|
M |
|
(z z |
) |
2 |
|
Q |
|
|
(z z |
)3 |
|
q |
|
(z z |
)4 |
|
|
|||||
|
|
|
доп i |
|
|
|
|
|
|
доп i |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
доп i |
|
|
i |
|
|
|
|
|
i |
|
|
, |
||||
|
|
|
z zi |
|
|
2EI |
|
|
|
|
|
6EI |
|
|
|
|
|
|
24EI |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где 0 , 0 , M 0 ,Q0 – прогиб, угол поворота, изгибающий момент, попе-
речная сила в начале координат (начальные параметры);
q0 – интенсивность равномерно распределенной нагрузки на первом участке;
n – число границ между участками; zi – абсцисса i-й границы участка;
M доп , Qдоп , qдоп – конечные приращения соответствующих величин на границах участков (дополнительные параметры);

 z zi – знак, указывающий, что все слагаемые, идущие по-
z zi – знак, указывающий, что все слагаемые, идущие по-
сле него, надо учитывать лишь тогда, когда z становится большим, чем zi – длины всех предшествующих участков балки.
6.1.4 Применение дифференциальных зависимостей между M, Q, q для построения эпюр усилий и определения нагрузок
Пример 6.1.3. По заданной эпюре моментов (рис. 6.6, а, б) построить эпюру Q и восстановить исходную нагрузку. Криволинейные участки эпюры очерчены по квадратным параболам с вершинами в отмеченных точках.
121
