
Задачник / Глава 02 (26-44)
.pdf
Глава 2 Осевое растяжение–сжатие
2.1 Теоретическая и методическая информация. Примеры
2.1.1Эпюры продольной силы
Вслучае осевого растяжения–сжатия в поперечных сечениях стержня возникает единственное внутреннее усилие – продольная сила N.
Для определения внутренних усилий в стержне применяется метод сечений, состоящий из следующих действий: рассекаем стержень сечением, перпендикулярным оси, отбрасываем одну из его частей, заменяем действие отброшенной части на оставленную усилием и уравновешиваем рассматриваемую часть стержня.
Эту последовательность действий легко запомнить с помощью аббревиатуры РОЗУ, образованной из первых букв выделенных в тексте слов.
Для построения эпюры N необходимо выполнить такие действия:
1)определить (если это необходимо) опорные реакции;
2)определить число участков;
3)для каждого из участков записать функцию продольной силы и построить ее график, т. е. эпюру N.
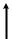 RВ
RВ
а |
|
F2 |
A2 |
b
 A1
A1
F1
z
Рис. 2.1
Пример 2.1.1. Дано: F1 = 3 кН; F2 = 5 кН;
=78,5 кН/м3; а = 3 м; b = 2 м; A1 = 10 см2; A2 = 20 см2 (рис. 2.1).
Построить эпюру N.
Решение. 1. Определение реакции в заделке RВ. Уравнение равновесия стержня:
Z 0; F1 A1b F2 A2a RB 0 RB F1 F2 A1b A2a
3 5 78,5 10 10 4 2 78,5 20 10 4 3
2,628 кН.
2.Участком называют часть стержня, на которой характер нагружения и функция продольной силы от z остаются неизменными. В данном примере стержень
имеет два участка.
3. Составим функции продольной силы на каждом участке и построим эпюру N.
26
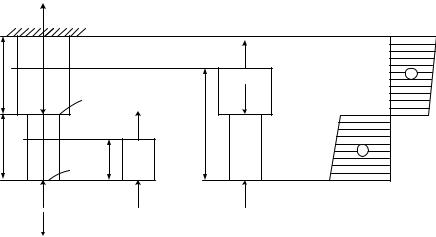
1-й у ч а с т о к . Мысленно рассекаем стержень в пределах первого участка сечением, имеющим координату z1. Функцию продольной силы определяем из условия равновесия нижней части стержня. Изобразим отсеченную часть (рис. 2.2, а, б).
а) |
Rb |
|
|
б) |
в) |
|
г) |
Эп. N, кН |
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
N2 |
|
|
2.63 |
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
+ |
|
F2 |
A |
2 |
|
F2 |
2.84 |
|
|
|
|
|
N1 |
|
|
2.16 |
||
|
|
|
|
2 |
|
|
||
|
|
|
|
|
z |
|
|
|
b |
|
|
|
|
|
|
- |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
F1 |
|
|
F1 |
F1 |
3 |
|
|
|
|
|
|
|
|
|||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.2 |
|
|
|
Продольную силу N в рассеченном стержне надо всегда показывать растягивающей, т. е. направленной от узла, от сечения. Тогда при определении продольной силы из условий равновесия она будет получаться положительной при растяжении стержня и отрицательной при сжатии, как это и установлено правилом знаков для внутренних усилий.
0 z1 b; N1 F1 A1z1 0;
N1 F1 A1z1 3 78,5 10 10 4 z1 3 0,0785z1.
Функция N1 линейная, следовательно, для построения эпюры продольной силы в пределах первого участка достаточно определить два зна-
чения |
функции |
N1, |
|
например |
в начале |
и |
конце |
участка: |
|||||
z1 0; |
N1 3 кН; z1 |
b 2 м; N1 3 0,0785 2 2,843кН. |
|||||||||||
2-й у ч а с т о к . Проводим сечение на втором участке и из условия |
|||||||||||||
равновесия отсеченной части (рис. 2.2, а, в) находим выражение для N2: |
|||||||||||||
b z2 |
b a; |
|
|
|
|
|
|
|
|
|
|||
N2 F2 F1 A1b A2 z2 b 0; |
|
|
|
|
|||||||||
N |
2 |
F F A b A |
z |
2 |
b 5 3 78,5 10 10 4 |
2 |
|||||||
|
|
2 |
1 |
1 |
2 |
|
|
|
|
|
|
||
78,5 20 10 4 z |
2 |
2 2,157 0,157 z |
2 |
2 . |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Продольная сила N2 – линейная. Определяем N2 |
в начале и в конце |
||||||||||||
второго участка: |
|
|
|
|
|
|
|
|
|
|
|||
z2 = 2 м; N2 = 2,157 + 0,157(2 – 2) = 2,157 кН;
27
z2 = 5 м; N2 = 2,157 + 0,157(2 + 3 – 2) = 2,157 + 0,471 = 2,628 кН.
По результатам подсчетов строится эпюра продольной силы по длине стержня. Ординаты на эпюре откладываются в масштабе (рис. 2.2, г). Скачки на эпюре N должны быть равны величине сосредоточенных сил, приложенных в сечениях.
Из решения видно, что если рассматривать равновесие отсеченной части со стороны свободного конца стержня, то реакцию RВ можно не определять предварительно. Она получится автоматически как ордината эпюры N в защемлении.
Решение уравнений равновесия отсеченных частей стержня позволяет заметить, что продольная сила в сечении равна сумме внешних сил, действующих на отсеченную часть, т. е. по одну сторону от проведенного сечения. Знак слагаемых при этом берется плюс, если сила вызывает растяжение, минус – в случае сжатия.
Учитывая это, в дальнейшем можно составлять выражения для продольной силы на каждом из участков, не изображая отсеченные части и не составляя уравнение равновесия для них.
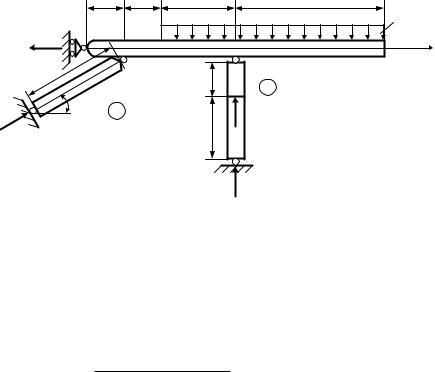
Пример 2.1.2. Дано: q = 10 кН/м; F = 40 кН; а = 1 м; = 30о;
CL – абсолютно жесткий стержень (рис. 2.3). Найти продольные силы N в стержнях 1 и 2.
|
а |
а |
2а |
|
4а |
R3 |
С |
|
В |
|
q |
|
|
х |
|||
|
|
|
|
||
а |
|
А |
а |
D |
L |
3 |
|
|
2 |
|
|
R1 |
|
|
|
|
|
|
1 |
|
F |
|
|
Е |
|
2а |
|
||
|
|
|
|
||
|
|
|
|
К |
|
|
|
|
|
R2 |
|
|
|
|
2.3 |
|
|
Рис. 2.3
Решение. 1. Определение опорных реакций:
M A 0; R2 3a F 3a q6a 4a 0;
R2 q6a 4a F 3a 10 2 4 40 40 кН; 3a
28
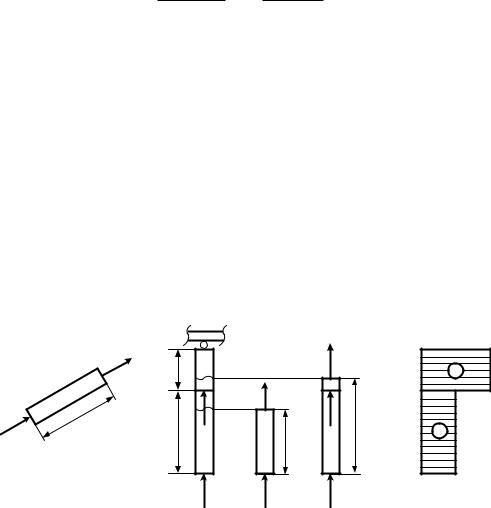
M D 0; q 6a a R1 sin 3a 0; |
|||||
R q6aa |
|
10 6 1 40 кН; |
|||
1 |
3a sin |
3 0, 5 |
|
|
|
|
|
|
|||
X 0; R3 R1 cos 0; |
R3 R1 cos 40cos30o 34,64кН. |
||||
Проверка: |
|
|
|
|
|
M B 0; R1a sin R2 2a F 2a q 6a 3a 0; |
|||||
40 0,5 1 40 2 40 2 180 0. |
|
|
|||
2. В опорном стержне АЕ – один участок, в стержне DK – два участ- |
|||||
ка. |
|
|
|
|
|
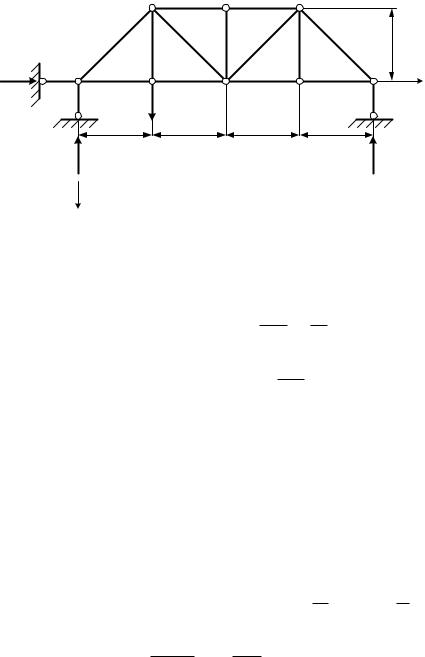
3. Определение продольной силы N. Рассекаем стержень АЕ и из |
|||||
уравнения равновесия нижней части находим (рис. 2.4, а): |
|||||
|
N R1 |
( 40) 40 кН. |
|
||
а) |
|
|
б) |
в) |
г) Эп. N, кН |
N |
а |
|
|
N2 |
- |
|
|
|
|
||
z |
|
|
N1 |
F |
80 |
|
F |
|
|
||
|
2а |
|
z2 |
- |
|
R1 |
|
z1 |
|||
|
|
|
|
||
|
|
|
|
|
40 |
|
R2 |
R2 |
R2 |
|
|
|
|
|
Рис. 2.4 |
|
|
Продольная сила по длине стержня АЕ постоянна, и она растяги- |
|||||
вающая. |
|
|
|
|
|
Стержень DK рассекаем в пределах первого участка и из уравнения |
|||||
равновесия нижней части определяем N1 (рис. 2.4, б): |
|
||||
0 z1 2a; N1 R2 40 кН. |
|
||||
На втором участке 2a z2 |
3a (рис. 2.4, в), |
|
|||
N2 R2 F 40 40 80 кН. |
|
||||
В пределах каждого из участков второго стержня эпюра N имеет по- |
|||||
стоянное значение (рис. 2.4, г). В сечениях стержня, где действуют силы |
|||||
R2 и F в эпюре N, наблюдаются ступенчатые изменения, равные по вели- |
|||||
чине приложенным силам. |
|
|
|
|
|
29
2.1.2 |
Продольные силы в стержнях фермы |
|
|
|
||||||||||||
Пример 2.1.3. Дано: h = 3 м; d = 4 м; F = 10 кН. |
|
|
|
|
|
|||||||||||
Определить усилия в стержнях фермы (рис. 2.5). |
|
|
|
|
|
|||||||||||
|
|
|
1 |
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
HA |
0 |
|
7 |
|
|
|
6 |
|
5 |
4 |
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
d |
|
|
|
d |
|
d |
|
|
|
|
|
|
|
VA |
|
|
|
|
|
|
|
|
|
RВ |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.5 |
|
|
|
|
|
|
|
|
|
||
Решение. 1. Определение опорных реакций: |
|
|
|
|
|
|
||||||||||
M A 0; |
RB 4d Fd 0; |
RB |
Fd |
F |
2,5 кН; |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
4d |
4 |
|
|
|
|
|
|
M B 0; VA 4d F 3d 0; VA |
3F |
7,5 кН; |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
X 0; H A 0. |
|
|
|
|
|
|
|
||||||
Проверка: Y 0; VA RB F 0; 7,5 2,5 10 0. |
|
|
|
|||||||||||||
2. Определение усилий в стержнях ферм. |
|
|
|
|
|
|
|
|||||||||
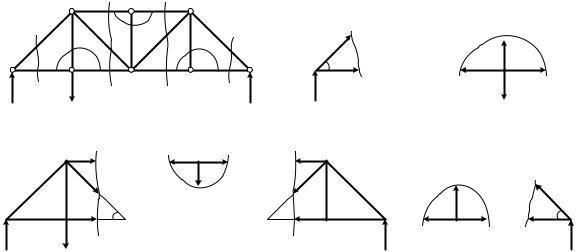
Предварительно пронумеруем узлы фермы (рис. 2.6, а). Проведем |
||||||||||||||||
сечение I–I, продольные силы в рассеченных стержнях предполагаем рас- |
||||||||||||||||
тягивающими, т. е. положительными. Из уравнений равновесия, состав- |
||||||||||||||||
ленных для узла 0 (рис. 2.6, б), определяем усилия в стержнях 0–1 и 0–7: |
||||||||||||||||
Y 0; N0 1 sin VA 0; |
|
arctg |
h |
arctg |
3 |
36 |
o |
|
|
|||||||
|
d |
4 |
|
45 ; |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
N0 1 |
|
VA |
|
7, 5 |
12, 5 кН; |
|
|
|
|
|
|||||
|
sin |
|
0, 6 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
X 0; |
N0 7 |
N0 1 cos 0; |
|
N0 7 |
N0 1 cos |
|
||||||||||
|
|
12,5 0,8 10 кН. |
|
|
|
|
|
|
|
|||||||
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
1 |
II |
2 |
III |
3 |
|
|
б) |
|
|
в) |
|
|
|
|
|
I |
|
|
|
|
|
IV |
|
|
|
|
N0-1 |
|
N7-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
7 |
|
|
|
6 |
5 |
4 |
|
0 |
|
N0-7 |
N0-7 |
|
7 |
N7-6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VA I |
F |
II |
|
III |
IV |
RВ |
|
|
VA |
|
|
|
F |
|
|
|
г) |
|
|
д) |
|
е) |
|
|
|
|
ж) |
|
|
з) |
|
||
|
1 |
N1-2 |
N1-2 |
2 |
N2-3 |
|
3 |
|
|
|
|
|
|
|||
|
|
N2-3 |
|
|
N3-5 |
|
|
N3-4 |
|
|||||||
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
N2-6 |
N |
-6 |
|
|
|
|
|
|
|
|
|
|
|
|
1-6 |
|
|
3 |
|
5 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
7 |
|
|
6 |
|
|
|
|
|
4 |
5 |
|
|
|
4 |
|
|
|
|
|
|
|
6 |
|
N5-6 |
|
N5-6 |
N4-5 |
N4-5 RВ |
|
|||
VA |
F |
N |
7-6 |
|
|
|
|
RВ |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Рис. 2.6 |
|
|
|
|
|
|
|
||
Для определения усилий N7-1 и N7-6 «вырежем» узел 7 (рис. 2.6, в):Y 0; N7 1 F 0; N7 1 F 10 кН;
X 0; N0 7 N7 6 0; N7 6 N0 7 10 кН.
Проведем сечение II–II (рис. 2.6, а) и из уравнения равновесия левой отсеченной части определим усилия N1-2 и N1-6 (рис. 2.6, г):
Y 0; |
N1 6 sin F VA 0; |
N1 6 |
|
F VA |
||||
|
|
10 7,5 |
|
|
|
|
sin |
|
|
|
4,17 |
кН; |
|
|
|
||
|
|
0,6 |
|
|
|
|
|
|
M 6 0; N1 2h VA 2d Fd 0; N1 2 |
|
VA 2d Fd |
|
|||||
|
|
h |
||||||
|
|
|
|
|
|
|
|
|
|
7,5 8 10 4 |
6,67 |
кН. |
|
|
|
||
|
|
3 |
|
|
|
|
|
|
Для определения N2-6 «вырежем» узел 2 (рис. 2.6, д):Y 0; N2 6 0.
Проведем сечение III–III (см. рис. 2.6, а) и из уравнений равновесия правой отсеченной части (рис. 2.6, е) определим усилия N2-3, N3-6, N5-6:
Y 0; N3 6 sin RB 0; |
N3 6 |
|
|
RB |
|
2, 5 |
4,17 |
кН; |
||||
|
sin |
0, 6 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
M 6 0; N2 3 h RB 2d 0; N2 3 |
|
RB |
2d |
|
2,5 8 |
6,67 кН; |
||||||
|
h |
|
3 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||
31

M 3 0; |
N5 6 h RB d 0; N5 6 |
RB d |
|
2,5 4 |
3,33 кН. |
|
h |
3 |
|||||
|
|
|
|
«Вырежем» узел 5 (рис. 2.6, ж) и определим усилие N3-5 :Y 0; N3 5 0.
Проведем сечение IV–IV и из уравнений равновесия правой отсеченной части определим усилия N3-4 и N4-5 (рис. 2.6, з):
Y 0; N3 4 sin RB 0; N3 4 RB 4,17 кН; sin
X 0; N3 4 cos N4 5 0; N4 5 N3 4 cos 3,33 кН.
2.1.3 Напряжения, подбор сечения и деформации при осевом растяжении–сжатии стержней
Р а с ч е т н ы е ф о р м у л ы :
для определения напряжения в поперечном сечении и условие проч-
ности при растяжении (сжатии): |
|
|
|
|
|
|
||
|
N |
; max |
|
Nmax |
|
, |
||
|
Aнетто |
|
||||||
|
A |
|
|
|
|
|||
где – допускаемое напряжение; |
Aнетто |
– наиболее ослабленное попе- |
||||||
речное сечение; |
|
|
|
|
|
|
||
для определения изменения длины на участке z: |
||||||||
|
|
z |
z |
Ndz |
|
|
||
|
|
0 |
|
, |
|
|
||
|
|
EA |
|
|
||||
здесь Е – модуль продольной упругости; частные случаи:
1) EA const , z N z ;
EA
2) EA const, N const, z EANz ,
при z l |
l |
Nl |
|
, |
|
EA |
|||||
|
|
|
|||
здесь N z площадь эпюры N на участке стержня длиной z;
A, Aнетто – площадь в любом и в наиболее ослабленном поперечном сечении стержня соответственно;
z – изменение длины стержня на участке от 0 до z;
32
l – длина стержня или его участка. |
|
|
|
|||||||||||||||||
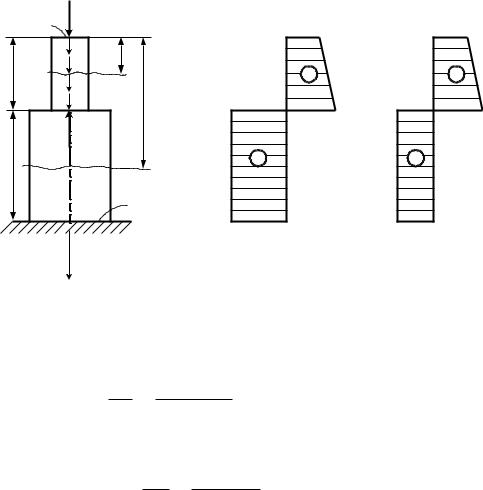
Пример 2.1.4. Дано: деревянный брус (рис. 2.7, а); F1 = 10 кН; F2 = |
||||||||||||||||||||
30 кН; q = 2 кН/м; а = 2 м; b = 3 м; A = 30 cм2; A =60 cм2; Е = 1 104 МПа. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
Требуется построить эпюру N и эпюру изменения нормальных на- |
||||||||||||||||||||
пряжений вдоль оси бруса, найти перемещение сечения I–I. |
||||||||||||||||||||
Решение. Стержень имеет два участка. Проводим на каждом из них |
||||||||||||||||||||
сечение и составляем уравнения для продольной силы: |
|
|||||||||||||||||||
0 z1 a; |
N1 F1 qz1; |
|
z1 0; |
N1 10 кН; |
||||||||||||||||
|
|
|
|
|
|
|
|
|
z1 2 м; N1 14 кН; |
|
|
|||||||||
|
|
|
a z2 |
a b ; N2 |
F1 qa F2 |
|
||||||||||||||
|
|
|
|
|
|
|
10 2 2 30 16 кН. |
|
||||||||||||
На первом участке N1 |
меняется линейно от минус 10 кН до минус |
|||||||||||||||||||
14 кН, на втором участке N2 – постоянная величина 16 кН. Строим по этим |
||||||||||||||||||||
данным эпюру N (рис. 2.7, б). |
|
|
|
|
|
|
|
|
||||||||||||
а) |
A |
1 |
F |
1 |
|
|
|
|
|
|
|
|
|
|
б) Эп. N, кН |
в) Эп. , МПа |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
q |
|
|
|
z1 |
|
|
I |
|
|
|
|
|
|
10 |
|
3,33 |
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
14 |
|
||
|
|
|
F2 |
|
|
|
|
|
|
|
|
|
|
|
4,67 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
2,67 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.7 |
|
|
|
|
||
Находим напряжения в сечениях z1 |
и z2: |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
N |
|
F qz |
|
|
10 2z1 |
10 3 |
, |
||||||
|
|
|
1 |
1 |
|
|
|
1 |
|
1 |
|
30 10 4 |
||||||||
|
|
|
|
|
A |
|
|
|
|
A |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
при z1 = 0 |
1 |
= 3,33 МПа; |
|
|
при z1 = а = 2 м 1 |
= 4,67 МПа; |
||||||||||||||
|
|
|
|
|
|
|
|
|
N |
2 |
|
16 10 3 |
2,67 |
МПа. |
|
|||||
|
|
|
|
|
|
2 |
|
|
60 10 4 |
|
||||||||||
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
Эпюра по длине стержня представлена на рисунке 2.7, в. |
|
|||||||||||||||||
Определяем перемещение верхнего сечения: |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
I I |
la lb , |
|
|
|
|
|
|
|
|||
где la |
и lb – изменение длины верхнего и нижнего участков стержня. |
|||||||||||||||||
В пределах каждого из участков жесткости EA1 и EA2 остаются по- |
||||||||||||||||||
стоянными, поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
l |
a |
Na ; l |
Nb ; |
|
Na |
Nb , |
|
|
|
||||||
|
|
|
|
|
|
b |
EA2 |
1 1 |
|
EA1 |
EA2 |
|
|
|
||||
|
|
|
|
|
|
EA1 |
|
|
|
|
|
|
||||||
где N |
|
, N |
– площади эпюры N на участках a и b соответственно. |
|
||||||||||||||
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I I |
|
(10 14) 2 10 3 |
|
|
16 3 10 3 |
|
|
|
|
||||||
|
|
|
2 |
1 104 30 |
10 4 |
1 104 |
60 10 4 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
0,8 10 3 0,8 10 3 |
0. |
|
|
|
|
|
|||||
Подсчет показал, что участок b удлинился, а участок a укоротился |
||||||||||||||||||
на одну и ту же величину. Таким образом, перемещения верхнего сечения |
||||||||||||||||||
не произошло. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 2.1.5. Дано: материал колонны |
(рис. |
2.8, |
а) – |
бетон; |
||||||||||||||
F1 = 600 кН; F2 |
|
= |
1000 кН; |
γ = 20 |
кН/м3; |
а |
= |
5 |
м; |
b = |
12 м; |
|||||||
Е = 1,5 104 МПа; |
|
= 5 МПа. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
а) |
|
|
F1 |
|
б) Эп. N, кН |
|
в) Эп. , МПа |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
I |
|
600 |
|
|
|
|
4,76 |
|
|
|||
|
|
|
|
|
|
|
z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
630,2 |
|
- |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
F2 |
|
|
|
1630,2 |
|
|
|
5,00 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
а |
|
|
|
z2 |
|
- |
|
|
|
|
|
|
4,90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1663,5 |
|
|
|
5,00 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.8 |
|
|
|
|
|
|
|
|
|
|
Требуется подобрать площадь сечения каждого из участков колонны |
||||||||||||||||||
Aa , Ab , построить эпюры изменения продольной силы N и напряжения σ |
||||||||||||||||||
по длине колонны; найти перемещение сечения I–I. |
|
|
|
|
|
|||||||||||||
Решение. Составим уравнение для продольной силы в произвольном |
||||||||||||||||||
сечении каждого из двух участков: |
|
|
|
|
|
|
|
|
|
|
||||||||
34
0 z1 b; N1 F1 Ab z1; |
(*) |
0 z2 a; N2 F1 Abb F2 Aa z2 , |
|
где N1 и N2 – линейно изменяющиеся функции. Наибольшее по модулю усилие на каждом из участков получим соответственно при z1 = b и z2 = а.
C другой стороны, из условия прочности имеем A . Следовательно,
|
|
N |
|
|
|
|
F1 Abb |
|
Ab ; |
Ab |
|
|
F1 |
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
1max |
|
|
|
b |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
600 |
|
0,126 |
м2; |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
103 20 12 |
|
Aa ; |
|
||||||||||||
|
|
|
|
N2max |
F1 Abb F2 Aa a |
|
|||||||||||||||||
A |
F1 |
Abb F2 |
|
600 20 12 0,126 1000 |
0,333 м2. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|||||||||||
a |
|
|
|
|
|
|
5 103 20 5 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
По зависимостям (*), учитывая найденные значения Aa и Ab, под- |
|||||||||||||||||||||||
считаем ординаты эпюры N: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
z1 0; |
N1 F1 600 |
кН; |
|
|
|
|
||||||||||||
z1 b 12 м; N1 |
600 20 12 0,126 630,2 кН; |
||||||||||||||||||||||
z2 0; N2 |
600 20 12 0,126 1000 1630,2 кН; |
||||||||||||||||||||||
z2 5 м; N2 |
600 20 12 0,126 1000 20 5 0,333 1663,5 кН. |
||||||||||||||||||||||
Эпюра N представлена на рисунке 2.8, б. Для построения эпюры нормальных напряжений N A надо ординаты эпюры N на участке b уменьшить в Ab раз, а на участке a – в Aа раз.
A надо ординаты эпюры N на участке b уменьшить в Ab раз, а на участке a – в Aа раз.
|
|
|
|
|
|
|
|
|
|
600 10 3 |
||||
|
|
z |
|
0, |
b |
|
|
|
4,76 МПа; |
|||||
|
|
|
|
|
||||||||||
|
|
1 |
|
|
|
|
|
|
0,126 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
630, 2 10 3 |
|||
z |
|
12 м, |
b |
|
|
|
|
5,00 МПа; |
||||||
|
|
|
|
|||||||||||
1 |
|
|
|
|
|
|
|
|
0,126 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1630, 2 10 3 |
|||||
|
z |
2 |
0, |
a |
|
|
|
|
|
4,90 МПа; |
||||
|
|
|
0,333 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1663,5 10 3 |
||||
z |
2 |
5 м, |
a |
|
|
|
|
|
5,00 МПа. |
|||||
|
0,333 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эпюра σ представлена на рисунке 2.8, в.
35
