МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ

БЕЛАРУСЬ

Гомельский государственный технический университет

имени П.О.Сухого

Кафедра физики

Лабораторная работа № 1-8

Выполнил студент гр. Э-13

Колесников П.М.

Принял преподаватель

Проневич О.И.

г. Гомель, 2001

Лабораторная работа № 1-8

Цель работы: Изучить сложение гармонических колебаний.

Приборы и принадлежности: звуковой генератор, осциллограф, прибор для исследования колебаний несвободных систем из набора приборов для лаборатории «Физические основы механики».

Теоретическая часть

1.

Данное уравнение называется дифференциальным уравнением гармонических колебаний, а система осуществляющая эти малые гармонические колебания называется линейным или гармоническим осциллятором.

(Линейным гармоническим осциллятором называется система, состоящая из материальной точки массой , совершающей прямолинейные гармонические колебания под действием упругой силы .)

2. Уравнение для системы, совершающей затухающие колебания:

Уравнение движения выражающее второй закон Ньютона будет иметь вид

, где ; ;

дифференциальное уравнение затухающих колебаний.

, где -амплитуда затухающих колебаний.

-собственная частота затухающих колебаний.

3. Затухающие синусоидальные колебания:

, где величина - амплитуда затухающих колебаний, - коэффициент затухания , - собственная частота затухающих колебаний.

Затухающие колебания представляют собой непериодические колебания. Если , то для характеристики затухающих колебаний используют логарифмический дескремент затухания - это натуральный логарифм отношения амплитуды отстоящих друг от друга на период:

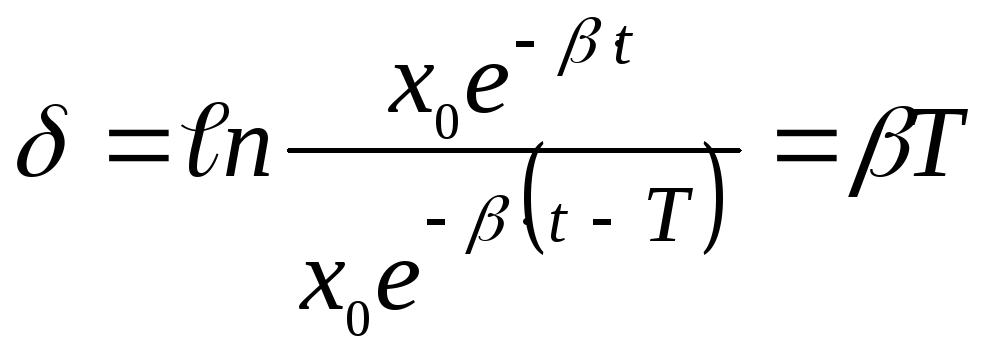
Если - такое движения системы не имеет колебательного характера и называется апериодическим.

2. Вынужденные колебания:

Уравнение движения выражающее второй закон Ньютона будет иметь вид

, где ; ;

- вынужденная сила.

, где

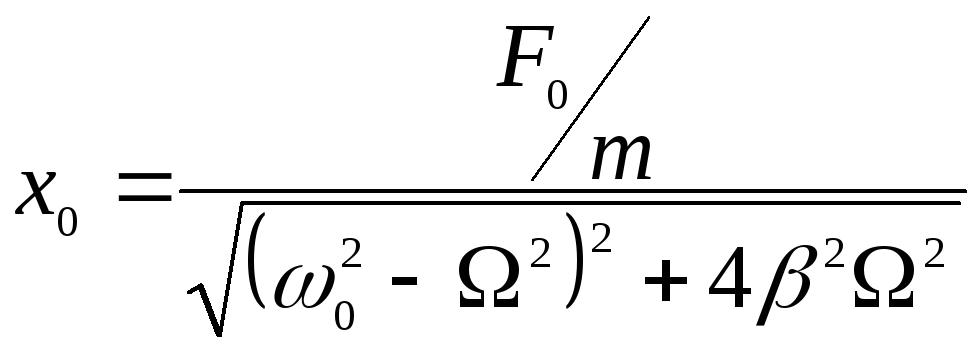
- разность фаз между смещением и возмущающей силой

при (резонансная частота).

2. Физический маятник:

- уравнение движения маятника в подвесе (в отсутствии силы трения), (из основного уравнения динамики вращательного движения )

при малых колебаниях

дифференциальное уравнение гармонических колебаний

Решением будет:

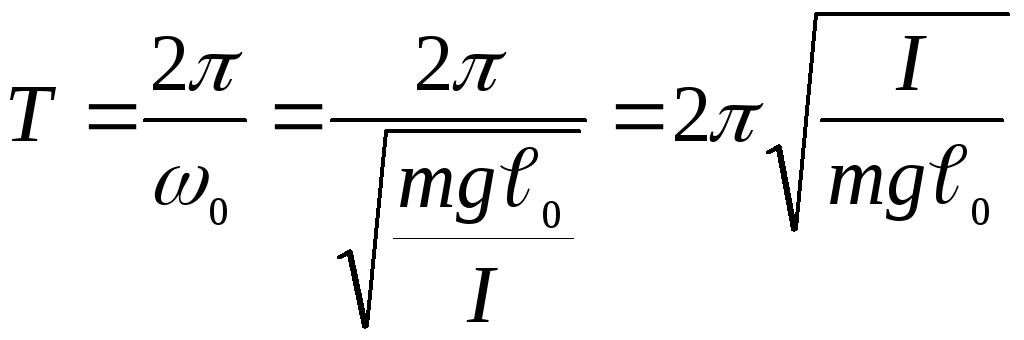
Оборотный маятник: , где

6. Дифференциальное уравнение колебания заряда Q в контуре:

В данном колебательном контуре внешнее э.д.с. отсутствует, поэтому рассматриваемые колебания представляют собой свободные колебания. Если сопротивление , то свободные электромагнитные колебания в контуре являются гармоническими.

Заряд Q совершает гармонические колебания по закону:

, где - амплитуда колебаний заряда конденсатора с циклической частотой , называемой собственной частотой контура:

8.

Если , , , то ,

9.

Сложение гармонических колебаний одинаковой частоты:

,

Искомый результат сложения колебаний:

(1)

(2)

, где и определяются из (1) и (2):

Сложение гармонических колебаний с близкими частотами биения:

,

Суммой двух гармонических колебаний с близкими частотами биения является колебание с изменяющейся амплитудой.

Сложение взаимно перпендикулярных колебаний вида:

, где - разность фаз колебаний.

- общее уравнение эллипса.

Ход работы

Если частоты двух перпендикулярных колебаний неодинаковы, и соотношение частот не выражается рациональным числом, то кривая не является замкнутой.

В случае рационального отношения частот будут иметь место различные кривые, вид которых зависит от отношение частот и сдвига начальных фаз (фигуры Лиссажу).

Если амплитуды колебаний равны А и B, то получающаяся фигура Лиссажу будет всегда ограничена прямоугольником со сторонами 2A и 2B.

1. Изменяя частоту генератора, получаем на экране фигуры Лиссажу, соответствующие отношению частот 2:1, 1:1, 1:2, 1:3. Записываем значение частот перестраиваемого генератора и зная отношение частот вычисляем :

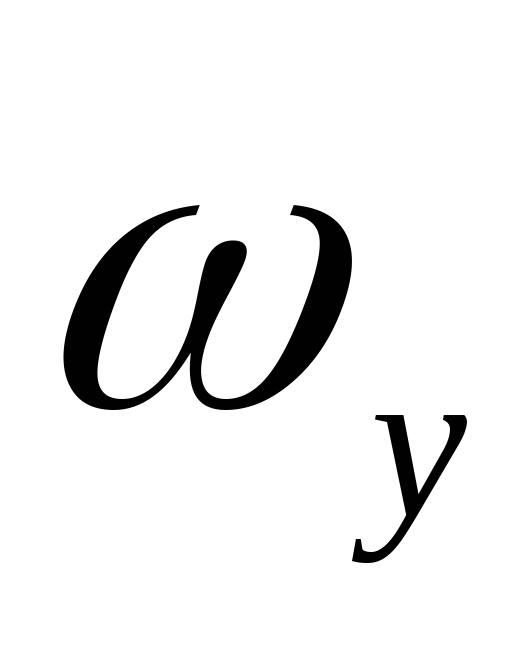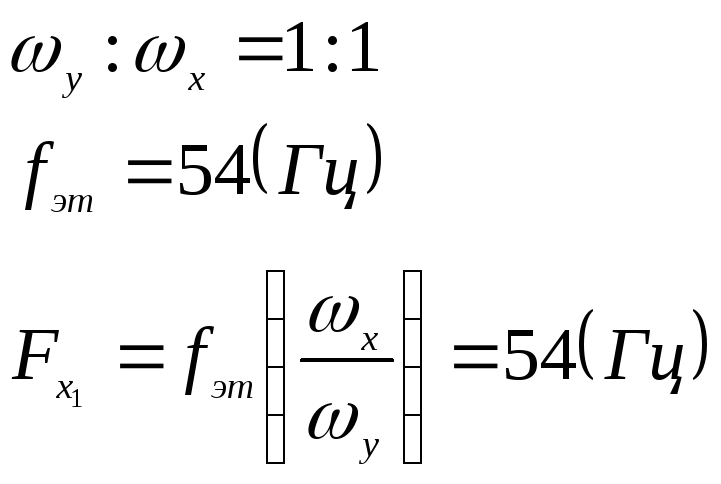
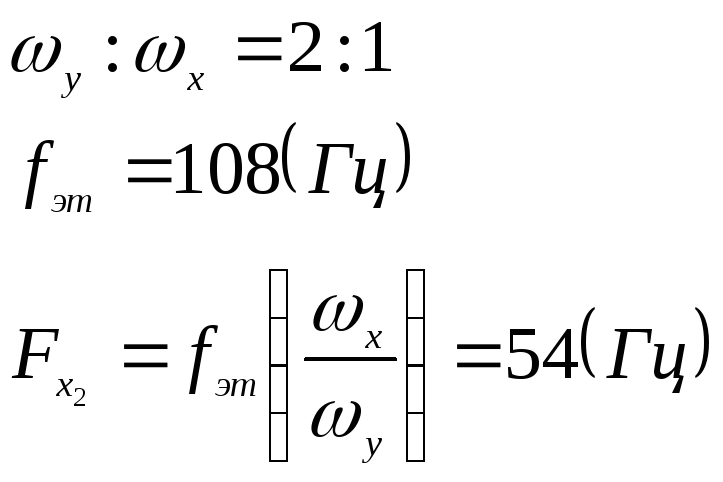
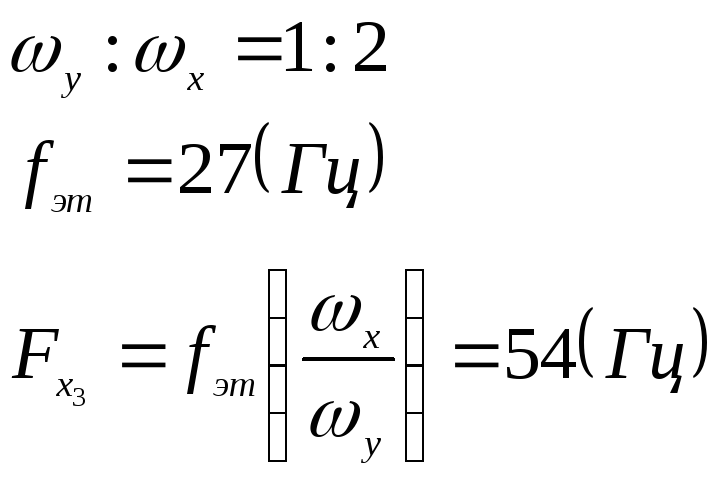
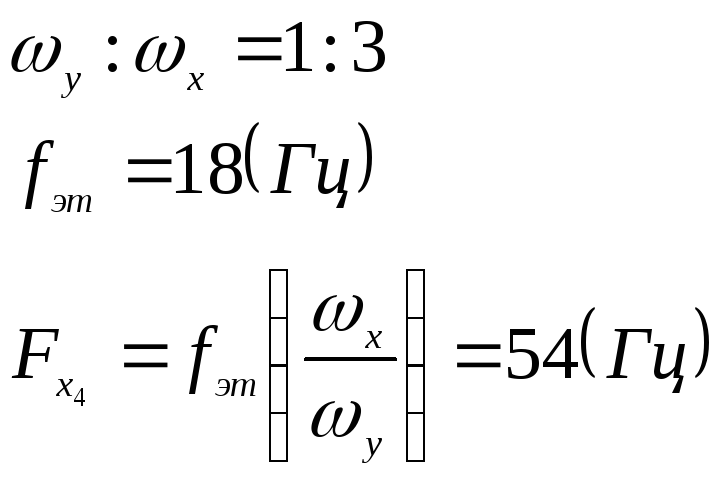
Вычисляем погрешность:

Вывод: В результате проделанной работы мы изучили сложение гармонических колебаний.