
Формула Байеса
Предположение об осуществлении какого-либо события А называют гипотезой (hypothesis). Гипотезы будем обозначать буквой Н.
Связь между гипотезами и событиями задаётся формулой Байеса. Формула вероятности гипотез была предложена в 18 веке.
Если
Н1,
Н2,…,Нn –
образуют полную группу несовместных
гипотез и произведено испытание, в
результате которого произошло событие
A,
то вероятность гипотезы после испытания
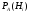 равна:
равна:
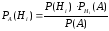 ,
,
где  -
вероятность
гипотезы
-
вероятность
гипотезы
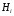 - априорная
вероятность гипотезы
- априорная
вероятность гипотезы
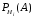 - условная вероятность
А при условии
- условная вероятность
А при условии
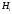
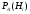 - апостериорная
вероятность гипотезы
- апостериорная
вероятность гипотезы
Р(А) – вероятность события А
Теорема Байеса (или формула Байеса) — одна из основных теорем элементарной теории вероятностей, которая позволяет определить вероятность какого-либо события при условии, что произошло другое статистически взаимозависимое с ним событие. Другими словами, по формуле Байеса можно более точно пересчитать вероятность, беря в расчет как ранее известную информацию, так и данные новых наблюдений.
Психологические эксперименты показали, что люди часто неверно оценивают апостериорную вероятность события, поскольку игнорируют его априорную вероятность. Поэтому правильный результат по формуле Байеса может сильно отличаться от интуитивно ожидаемого.
Теорема Байеса названа в честь Томаса Байеса (1701-1761) - человека, который первый предложил использование теоремы для корректировки убеждений, основываясь на обновленных данных.
Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной.
События, отражающие действие «причин», в данном случае называют гипотезами, так как они – предполагаемые события, повлекшие данное. Безусловную вероятность справедливости гипотезы называют априорной (насколько вероятна причина вообще), а условную – с учетом факта произошедшего события – апостериорной (насколько вероятна причина оказалась с учетом данных о событии).
В задачах Р(А) обычно вычисляется по формуле полной вероятности события, зависящего от нескольких несовместных гипотез, имеющих суммарную вероятность 1.
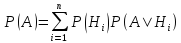
Вероятность
события А, которое может наступить
только при условии появления одного из
событий (гипотез) Н1,
Н2,
…, Нn,
образующих полную группу попарно
несовместных событий, равна сумме
произведений вероятностей каждого из
событий
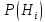 на
соответствующую условную вероятность
события А.
на
соответствующую условную вероятность
события А.
Вероятности под знаком суммы известны или допускают экспериментальную оценку.
Формула Байеса используется при машинной диагностике заболеваний. Предполагаемые заболевания считаются гипотезами, а наблюдаемые симптомы (факты) – событиями.
Пример. Из 10 студентов, пришедших на экзамен, 3 подготовлено отлично, 4 – хорошо, 2 – посредственно и 1 – плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный – на 16 вопросов, посредственно – на 10, плохо – на 5 вопросов. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что этот студент подготовлен отлично.
Решение. Введем события: A – студент ответил на три заданных вопроса, H1 – студент подготовлен отлично, H2 – студент подготовлен хорошо, H3 – студент подготовлен посредственно, H4 – студент подготовлен плохо. Эти гипотезы образуют полную группу несовместных событий.
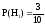 ,
,
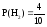 ,
,
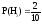 ,
,
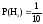 .
.
Контроль: 0,3+0,4+0,2+0,1=1.
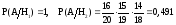 ,
,

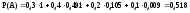 .
.
Искомая
вероятность
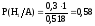 .
.
Пример. Два охотника одновременно стреляют одинаковыми пулями в медведя. В результате медведь был убит одной пулей (событие А). Как охотники должны поделить шкуру убитого медведя, если известно, что вероятность попадания у первого охотника 0,3,а у второго 0,6?
Решение:
Воспользуемся формулой Байеса. Определим предварительно гипотезы.
Гипотеза H1 попал первый охотник, второй промахнулся.
Гипотеза H2: попал второй, первый промахнулся.
Гипотеза H3: попали оба охотника.
Гипотеза H4: оба промахнулись.
Событие А может произойти только тогда, когда произошла либо гипотеза H1 либо гипотеза H2, т. е.:
Р(А/H1) = 1, Р(А/H3) = 0,
3Р(А/Н2) = 1 Р(А/Н4) = 0.
Предполагаем, что попадания охотников в медведя не зависят друг от друга. И получаем:
P(H1) = 0,3(1 -0,6) = 0,12
Р(Н2) = 0,6(1 -0,3) = 0,42;
P(H3)= 0,3·0,6 = 0,18;
Р(Н4) = (1-0,3)(1 -0,6) = 0,28.
Применяем формулу Байеса:
P(H1/А)
=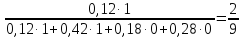
P(H2/А)
=
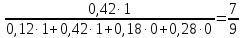
Таким образом, при справедливом делении первый охотник должен получить 2/9 шкуры, т.е. меньше четвертой части шкуры, в то время как, на первый взгляд, казалось, что ему причитается 1/3 шкуры (0,3).
Основные понятия комбинаторики
Комбинаторика – раздел математики, в котором изучаются задачи выбора элементов из заданного множества и размещения этих элементов в каком-либо порядке.
Перестановкой из n элементов называется каждая последовательность этих элементов в каком–либо порядке. Перестановки отличаются друг от друга только порядком следования элементов.
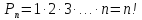
1!=1 0!=1
Число возможных перестановок букв a, b, c равно 6: abc, acb, bac, bca, cab, cba
P3=3!=1 =6
=6
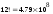
P12=1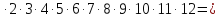 4,79
4,79
 108
=479
108
=479
 106=479
106=479
 1000
000 =479 000 000
1000
000 =479 000 000
Размещениями из n элементов по k в каждом называются такие последовательности, каждое из которых содержит k элементов, взятых из числа данных n элементов, которые отличаются друг от друга либо самими элементами, либо порядком их расположения
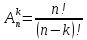
Пример. В конкурсе медсестёр участвуют 12 человек. Имеется три призовых места. Сколько имеется вариантов распределения призовых мест?
Решение. В задаче имеют значение и выбор участников, и распределение мест между ними. Необходимо найти размещение из 12 элементов по 3.
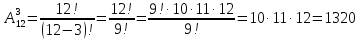
Последовательности, в которых не надо учитывать порядок следования элементов называются сочетанием.
Сочетанием из n элементов по k называются любые последовательности из k элементов, входящих в число данных n элементов, и отличающихся друг от друга хотя бы одним элементом

Пример. В клетке содержится 10 мышей. Необходимо отобрать 4 мыши для проведения эксперимента. Сколькими способами это можно сделать?
Решение. Так как порядок выбранных мышей не имеет значения, то вычислим число сочетаний из 10 по 4.
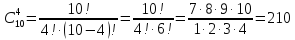
Независимые испытания. Формула Бернулли
При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.
Примеры повторных испытаний:
1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;
2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается).
Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А в единичном испытании буквой р, т.е. p=P(A), а вероятность противоположного события – буквой q, q =1−p.
Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли
![]() ,
где
,
где
![]()
![]()
![]()
Формула Бернулли позволяет избавиться от большого числа вычислений – сложения и умножения вероятностей – при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли, выведшего формулу.
Распределение числа успехов (появлений события) носит название биномиального распределения.
Пример 1. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.
Решение. Событие А – достали белый шар. Тогда вероятности
![]() ,
, ![]() .
.
По формуле Бернулли требуемая вероятность равна
![]() .
.
Пример 2. Определить вероятность того, что в семье, имеющей 5 детей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
Решение. Вероятность рождения девочки
![]() ,
тогда
,
тогда ![]() .
.
Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Следовательно, искомая вероятность
![]() .
.
Пример 3. Независимые
испытания продолжаются до тех пор, пока
событие А не произойдет k раз.
Найти вероятность того, что
потребуется n испытаний, если в
каждом из них![]() .
.
Решение. Событие В – ровно n испытаний до k-го появления события А – есть произведение двух следующий событий:
D – в n-ом испытании А произошло;
С – в первых (n–1)-ом испытаниях А появилось (к-1) раз.
Теорема умножения и формула Бернулли дают требуемую вероятность:
![]()
