3. Затухающие колебания
В любой реальной
колебательной системе происходят потери
энергии. Поэтому, если отсутствуют
внешние источники энергии, амплитуда
колебаний будет уменьшаться. Чем больше
амплитуда, тем больше потери энергии;
другими словами, скорость уменьшения
амплитуды пропорциональна самой
амплитуде:
.Знак «минус» показывает, что амплитуда
уменьшается: коэффициентβназывается
коэффициентом затухания. Это
дифференциальное уравнение легко
решить:
;
lnA – lnAo
= –βt; A
= Aoe–βt,
где Ао – начальная амплитуда (приt= 0). Видно, что амплитуда уменьшается по экспоненциальному закону.
Подставляя выражение для амплитуды в формулу гармонических колебаний, получим формулу затухающего колебания:
x(t) = x0 е–βtcos(ωзt).
Следует отметить,
что частота затухающих колебаний не
равна собственной частоте ω0:
.
График затухающих колебаний выглядит так:
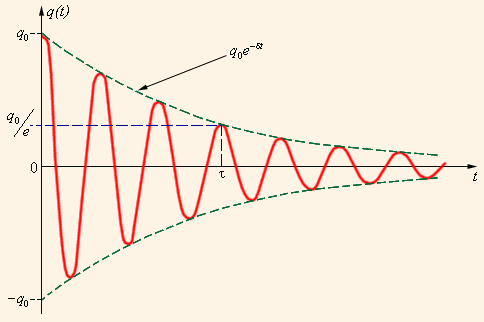
Если провести линии через точки максимального отклонения (пунктир), получатся экспоненты, соответствующие полученной выше формуле.
Скорость уменьшения амплитуды зависит от величины коэффициента затухания β. Из формулы легко видеть, чтоβопределяетуменьшение амплитуды за единицу времени(одну секунду). Размерность коэффициента затухания – с-1. Можно дать и другое определение коэффициента затухания. Это величина, обратная времени, за которое амплитуда колебания уменьшается вeраз (τ– постоянная времени).
Из смысла коэффициента
затухания ясно, что значение β
определяется величинами, влияющими
на потери энергии в системе. Для
механических колебаний это трение (
,
гдеr – коэффициент
трения).
На практике часто нагляднее показывать уменьшение амплитуды за один период.Декремент затухания– это величина, равная отношению амплитуд двух колебаний, отстоящих друг от друга на один период: θ =А(t)/A(t+T).
Понятие декремента
нередко встречается в биофизике и
физиологии. Например, говорят, что
возбуждение может распространяться по
мембране клетки с декрементом (то есть
с затуханием) или без декремента (без
затухания).
Так как затухание колебаний происходит по экспоненциальному закону, для расчётов часто удобно пользоваться понятием логарифмического декремента δ:
δ = ln θ = ln(A(t)/A(t+T) = ln(eβt) = βt или δ = βt
4. Уравнение волны
Волны – это колебания, распространяющиеся в пространстве и переносящие с собой энергию. Перенос энергии — принципиальное отличие волн от колебаний, в которых происходят лишь «местные» преобразования энергии. Волны же, как правило, способны удаляться на значительные расстояния от места своего возникновения (по этой причине волны иногда называют «колебанием, оторвавшимся от излучателя»).
Рассмотрим волну, возникающую на поверхности жидкости под воздействием колебаний длинного цилиндрического стержня:
y(t) = ymax cos(ωt)
где ymax=A - амплитуда колебаний цилиндра, ω=2πν, где ν - частота колебаний, t - время.
Если волна распространяется без затухания, то любая точка поверхности жидкости будет колебаться с той же амплитудой, что и стержень, но фаза колебаний будет изменяться пропорционально расстоянию от него. Это связано с тем, что волна распространяется с конечной скоростью, и в точку, расположенную на расстоянии x от источника колебаний она придет с временной задержкой τ = x/V. Соответственно, фаза колебаний в точке х будет равна φ=ω(t – τ) = ω(t – x/V), а уравнение волны, позволяющее рассчитать состояние системы в любой момент времени в любой точке пространства имеет вид: y(t)=ymax сos ω(t – x/v).
Геометрически у волны выделяют следующие элементы:
гребень волны - множество точек волны с максимальным положительным отклонением от состояния равновесия;
долина (ложбина) волны - множество точек волны с наибольшим отрицательным отклонением от состояния равновесия;
фронт волны — множество точек, имеющих в некий фиксированный момент времени одинаковую фазу колебаний. В зависимости от формы фронта волны выделяют плоские, сферические, эллиптические и другие волны.
В отличие от стационарного колебанияволны имеют две основные характеристики:
временну́ю периодичность - скорость изменения фазы с течением времени в какой-то заданной точке, называемую частотойволны ν ;
пространственную периодичность — скорость изменения фазы в определённый момент времени с изменением координаты - длина волны λ.
Длина волны соответствует расстоянию между соседними гребнями (долинами) волны. С другой стороны, длина волны – есть расстояние, которое волна проходит за один период. Соответственно, λ=VT=V/ν.