ВОПРОСЫ НА ЭКЗАМЕН

1. Определение целей и задач статистического исследования

Цель статистического исследования, как и любого научного исследования, — раскрыть сущность массовых явлений и процессов, а также присущие им закономерности. Отличительная особенность этих закономерностей в том, что они относятся не к каждой отдельной единице совокупности, а ко всей массе единиц в целом.

Задача статистического исследования состоит в получении обобщающих показателей и выявлении закономерностей общественной жизни в конкретных условиях места и времени, которые проявляются лишь в большой массе явлений через преодоление случайности, свойственной единичным элементам. Чтобы охарактеризовать массовое общественное явление или процесс в целом, необходимо рассмотреть всю или очень большую массу относящихся к ним отдельных явлений и процессов.

Цель исследования – получение новых сведений.

В исследовании нужно решить определенные задачи:

1. Необходимо выбрать критерии оценивания степени возможной связи выбранных целевых функций и факторов

2. Выбрать метод обработки реальной информации, от которой зависят возможности предстоящего оценивания и которая требует определенной систематизации обрабатываемой информации (план исследования в виде матрицы планирования)

3. Произвести подбор информации в соответствии с требованиями, выбранным на предыдущем этапе методом. Выполнение этого этапа представляется в виде матрицы результатов, которые являются одновременно матрицей исходных данных для последующих компьютерных расчетов

4. Разработать или подобрать ПО. Ввести информацию и произвести обработку данных

5. Анализ полученных данных и принятие решения либо о значимости, либо о недостаточной надежности произведенных расчетов и путях их доработки и совершенствования в повторных операциях.

2. Планирование статистического эксперимента. Эксперимент и наблюдательное исследование. Простая случайная выборка. Отклонения в выборках и их классификация.

Под статистическим планированием эксперимента будем понимать такую организацию экспериментального исследования, которая позволит собрать необходимые данные, применить для их анализа статистические методы и сделать правильные и объективные выводы.

Наблюдательное исследование – объективная необходимость получения новых сведений о взаимосвязях, свойствах или иных характеристиках некоторого конкретного объекта. Исследователь собирает данные путём простого наблюдения событий в их естественном течении, не вмешиваясь в них активно. Противоположностью обсервационному исследованию является эксперимент.

Эксперимент — это система познавательных операций, которая осуществляется в отношении объектов, поставленных в такие условия (специально создаваемые), которые должны способствовать обнаружению, сравнению, измерению объективных свойств, связей, отношений объектов и (или) проверке истинности теории в отношении этих свойств, связей, отношений. Он предполагает вмешательство в естественные условия существования предметов и явлений или воспроизведение определенных сторон предметов и явлений в специально созданных условиях с цепью изучения их без осложняющих процесс сопутствующих обстоятельств.

Простой случайный отбор предполагает, что вероятность быть включенным в выборку известна и является одинаковой для всех единиц совокупности. Он реализуется двумя методами:

♦ отбор вслепую (другое название — метод лотереи или жребия),

♦ отбор не вслепую (происходит с помощью таблицы случайных чисел). Итак, в одном случае вы осуществляете свой выбор не глядя, в другом - все осознавая, но для того чтобы самому не вмешаться и ничего не испортить, обращаетесь к специальным таблицам.

Различают простую случайную повторную выборку (после отбора какой-то единицы она снова возвращается в совокупность) и простую случайную бесповторную выборку (отобранная единица не возвращается в совокупность и вероятность попадания оставшихся единиц возрастает).

Среднеквадратическое отклонение— в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания.

Стандартное отклонение (оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии) s:

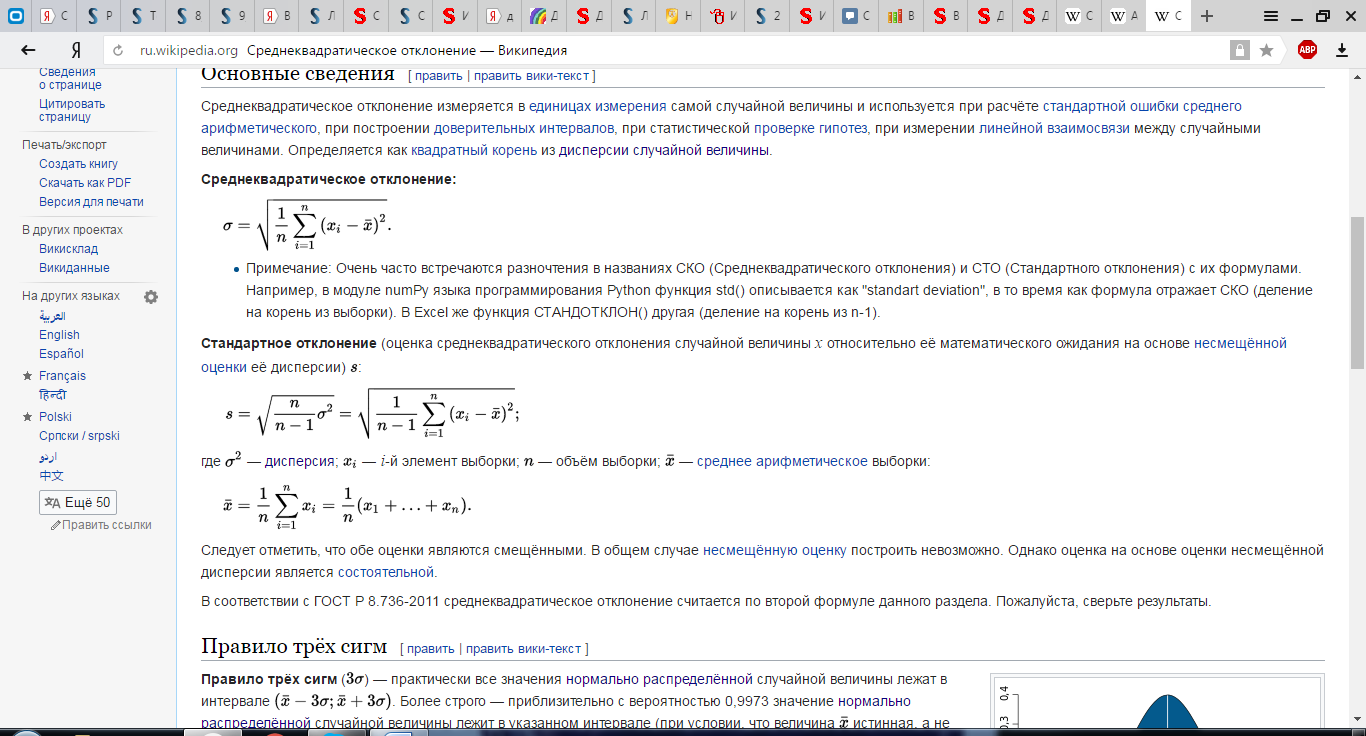
Где σ²— дисперсия, x_i— i-й элемент выборки, n — объём выборки;x с чертой— среднее арифметическое выборки:

Правило трёх сигм (3σ) — практически все значения нормально распределённой случайной величины лежат в интервале (х с чертой-3σ; х с чертой+3σ).