Математические методы / Лабораторные / Лабораторная №4 Вариант №17

МІНІСТЕРСТВО ОСВІТИ І НАУКИ

НАЦІОНАЛЬНИЙ АВІАЦІЙНИ УНІВЕРСИТЕТ

ІНСТИТУТ КОМП'ЮТЕРНИХ ІНФОРМАЦІЙНИХ ТЕХНОЛОГІЙ

Лабораторна робота №4

З дисципліни:”Математичні методи дослідження операцій”

Виконав студент групи ТП – 213:

Односумов Микола

Перевірив: Моржов В.І. ______

Київ 2017

Разработать программу и выполнить расчет координат экстремального значения нелинейной двумерной целевой функции на базе ЦВМ методом Золотого сечения с покоординатным смещением.

В процессе выполнения домашнего задания необходимо:

1. Построить графическое отображение двумерной поверхности целевой функции, заданной массивом чисел – 1 балл.

2. Проанализировать характер целевой функции и дать описание ее основных характеристик – 1 балл.

3. Дать описание численного метода, который используется для расчета экстремального значения целевой функции – 1 балл.

4. Разработать алгоритм вычислительного процесса для определения численного значения экстремума двумерной целевой функции – 2 балла.

5. Разработать программу на любом алгоритмическом языке программирования – 4 балла.

6. Отладить на ЦВМ и выполнить контрольные расчеты, подтверждающие правильность работы программы – 2 балла.

7. Оформить отчет по выполнению лабораторной работы №4– 1 балл.

8. Защитить лабораторную работу №4 – 2 балла.

Вариант №17

Таблица нелинейной целевой функции F(x,y).

X Y	-40	-35	-30	-25	-20	-15	-10	-5	0	5	10	15	20	25	30
0	55	50	45	40	35	30	25	20	15	20	25	35	40	45	50
3	50	45	40	35	30	25	20	15	10	15	20	30	35	40	45
6	45	40	35	30	25	20	15	10	5	10	15	25	30	35	40
9	35	30	25	20	15	10	5	3	1	3	5	10	15	20	30
12	40	35	30	25	20	15	10	5	2	2,5	5	10	15	20	25
18	45	40	35	30	25	20	15	10	5	10	15	20	25	30	35
21	50	45	40	35	30	25	20	15	10	15	20	25	30	35	40
24	60	50	45	40	35	30	25	20	15	20	25	30	35	40	50

Графічне відображення.

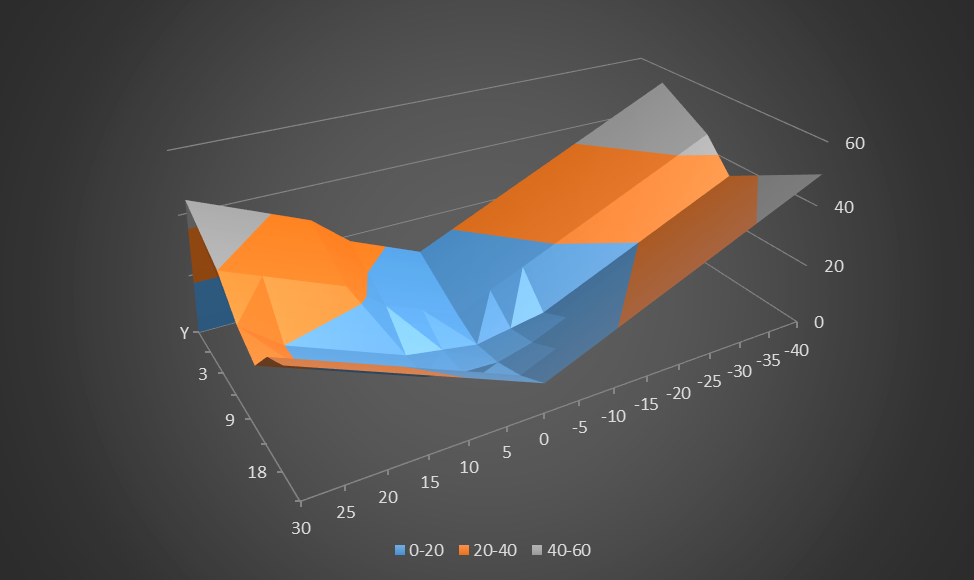
Для того, щоб знайти найменше значення функції на поверхні, необхідно використати метод градієнтного спуску (у моєму випадку можна використовувати метод з постійним кроком) для кожного із 8 графіків, і маєчи точки екстремуму, вибрати з них найменшу. Або використати метод покомпонентного спуску.

Теоретичні відомості методу покомпонентного спуску.

Для нахождения минимального локального элемента используем метод золотого сечения. Метод золотого сечения — метод поиска экстремума действительной функции одной переменной на заданном отрезке. В основе метода лежит принцип деления отрезка в пропорциях золотого сечения. Является одним из простейших вычислительных методов решения задач оптимизации. Впервые представлен Джеком Кифером в 1953 году.

Текст програми.

private final static double PHI = (1 + sqrt(5)) / 2; public static void main(String[] args) throws FileNotFoundException { double[][] arr = readFromFile("data.txt"); double[] answer = findMinimalElement(arr); System.out.printf("Найдено минимальное значение.\n" + "f(x,y)=%.2f Xi=%.1f Yj=%.1f", answer[0], answer[1], answer[2]); } private static double[] findMinimalElement(double[][] arr) { double[] indexesAndElement; double elementX = 0; double elementY = 0; double tempMin = arr[1][1]; for (int i = 1; i < arr.length; i++) { for (int j = 1; j < arr[i].length; j++) { if (tempMin > arr[i][j]) { tempMin = arr[i][j]; elementX = arr[0][j]; elementY = arr[i][0]; } } } indexesAndElement = new double[]{tempMin, elementX, elementY}; return indexesAndElement; } private static double[][] readFromFile(String fileName) throws FileNotFoundException { BufferedReader reader = new BufferedReader(new InputStreamReader(new FileInputStream(fileName))); ArrayList<String> lines = new ArrayList<>(); reader.lines().forEach(lines::add); double[][] numbers = new double[lines.size()][lines.get(0).split("\\s+").length]; for (int i = 0; i < lines.size(); i++) { String[] strNumbers = lines.get(i).split("\\s+"); for (int j = 0; j < strNumbers.length; j++) { numbers[i][j] = Double.parseDouble(strNumbers[j]); } } return numbers; }

Результати виконання програми.

Відповідь: F(x,y)=1, Xi=0, Yj=9

Висновок: під час виконання лабораторної роботи із заданого масиву значень функцій і їх змінних було побудовано графіки; проаналізовано функції; розглянуто метод золотого сечения с покоординатным смещением; розроблено алгоритм визначення чисельного значення екстремуму функції; розроблено програму згідно із методом пошуку мінімального значення у нашому випадку; відлагоджено роботу програми і виконано контрольні розрахунки, підтверджуючі правильність роботи програми;