- •Глава 2.Дифференциальные уравнения первого порядка, интегрируемые в квадратурах
- •§1. Уравнения с разделяющимися переменными
- •Решение типовых примеров
- •Задачи для самостоятельного решения
- •§2. Однородные уравнения
- •Решение типовых примеров
- •Задачи для самостоятельного решения
- •Дифференциальные уравнения, приводимые к однородным задачи с решениями
- •Задачи для самостоятельного решения
Решение типовых примеров
Задача.Найти форму зеркала, собирающего параллельные лучи в одну точку, обладающую указанным свойством.
За
ось ОХвыберем прямую, параллельную
лучам, а за начало координат ‑ точку,
в которой пересекаются все лучи после
отражения. Если LM
(рис. 1) ‑ луч, падающий на кривую
и попадающий после отражения в точкуО, то (по закону оптики угол падения
равен углу отражения) углы![]() и
и![]() ,
которые образуют лучиLMиМОс
касательнойТМ к кривой в точкеМ,должны быть равны. Вследствие этого
треугольникОТМравнобедренный, а
потому ТО=ОМ.
,
которые образуют лучиLMиМОс
касательнойТМ к кривой в точкеМ,должны быть равны. Вследствие этого
треугольникОТМравнобедренный, а
потому ТО=ОМ.
Е сли
сли
![]() ‑ координаты точкиМ,то
‑ координаты точкиМ,то![]() .
ОтрезокОТ,представляющий абсциссу
точкиТ, в которой касательная
пересекает осьОx,
находим из уравнения касательной:
.
ОтрезокОТ,представляющий абсциссу
точкиТ, в которой касательная
пересекает осьОx,
находим из уравнения касательной:
![]() .Возьмем
.Возьмем ![]() .
.
Рис.1
![]() .
Следовательно,
.
Следовательно,
![]()
Подставляя в (*), получаем дифференциальное уравнение задачи:
![]() .
.
Написав его в симметрической форме:
![]() •(а)
•(а)
видим,
что оно является однородным. Применяем
подстановку
![]() .
Тогда
.
Тогда
![]() .Подставляя в (а), получаем:
.Подставляя в (а), получаем:
![]()
Разделяем переменные и интегрируем:
![]() ;
;
![]() ;
;
![]() (б)
(б)
Далее
разрешаем (б) относительно иследующим
приемом:![]() ;
умножая числитель и знаменатель дроби
;
умножая числитель и знаменатель дроби![]() на сопряженное со знаменателем выражение,
получаем:
на сопряженное со знаменателем выражение,
получаем:
![]() .
(в)
.
(в)
Складывая
(б) и (в), находим;![]()
![]() .
.
Обозначая
![]() ,получаем окончательно:
,получаем окончательно:
![]() .
.
Решением служит парабола, ось симметрии которой ‑ ось Ox, a фокус лежит в начале координат. Таким образом, ось искомой параболы параллельна пучку лучей, а фокус параболы лежит в оптическом фокусе.
Вращая такую параболу вокруг оси ОХ,находим искомую зеркальную поверхность ‑ параболоид вращения.
Очевидно, что если источник света поместить в начале координат (фокусе), то лучи после отражения пойдут параллельным пучком. В силу этого зеркалу прожектора придается форма параболоида вращения.
Пример 1. Решить
уравнение![]() .
.
Решение:![]() Проверим однородность уравнения:
Проверим однородность уравнения:![]() Сделаем замену:
Сделаем замену:
![]() .
.
Подставим
в исходное уравнение:
![]() (получим уравнение с разделяющимися
переменными)
(получим уравнение с разделяющимися
переменными)![]()

![]() .
.![]()
![]()
![]()
Ответ:
![]()
Пример 2.![]() .
.
Решение:![]()
![]()

![]() .
.
Ответ:![]() .
.
Пример 3.![]() .
.
Решение:![]()
![]()
 ,
,
![]() ,
,![]()
![]()
Ответ:![]() .
.
Пример 4.Решить
уравнение![]()
Решение:![]()
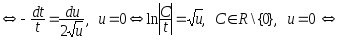

![]()
Ответ:![]() .
.
Пример 5.Решить
уравнение![]() .
.
Решение:![]()
![]()
![]()
![]()
![]()
![]() C
R\{0}, 1+2u-u2=0
x2(1+2u-u2)=C,
CR
C
R\{0}, 1+2u-u2=0
x2(1+2u-u2)=C,
CR
![]() .
.
Ответ:![]() .
.
246.![]()
Решение:![]() x=0,
x=0,
![]()
![]()
![]()
![]()
![]()
![]() (C
R\{0}),
(C
R\{0}),
![]()
![]() С
R\{0}.
С
R\{0}.
Ответ:
![]() С R\0,
x=0.
С R\0,
x=0.
247.
![]()
Решение:![]() х=0, у=их,
х=0, у=их,
![]()
![]()
![]()
![]()
![]() СR\{0},
СR\{0},
![]() CR\{0}
CR\{0}
![]() ,
CR\{0},
x=0
C= 0
C
R.
,
CR\{0},
x=0
C= 0
C
R.
Ответ:
![]() ,С R.
,С R.
248.
![]()
Решение:
![]()
![]()
![]()
![]()

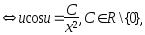
![]() (
(![]()
![]() x=0)
x=0)![]() .
.
Ответ:![]()
![]() .
.
Пример
9. Решить уравнение
![]()
Решение:![]() ,
,
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
Ответ:![]() .
.
Пример
10. Решить уравнение
![]() .
.
Решение:![]()
![]()

![]() Ответ:
Ответ:![]()
Пример 11.![]()
Решение:![]()
![]()


Ответ:![]()
Пример 12.Решить уравнение![]()
Решение:
![]()
![]()

![]()
![]()
![]()
Ответ:![]()
Пример 13.Решить уравнение![]()
Решение:![]()


Ответ:
Пример 14.![]()
Решение:![]()
![]()

Ответ:
Пример 15.![]()
Решение:![]()
![]()
![]()
Ответ.![]()
Задачи для самостоятельного решения
1.
![]() Ответ:
Ответ:
2.
![]() Ответ:
Ответ:![]()
3.
![]() Ответ:
Ответ:![]()
4.
![]() Ответ:
Ответ:![]()
5.
![]() Ответ:
Ответ:![]()
6.
![]() Ответ:
Ответ:![]()
7.
![]() Ответ:
Ответ:![]()
8.
![]() Ответ:
Ответ:![]()
9.
![]() Ответ:
Ответ:![]()
10.
![]() Ответ:
Ответ:![]()
11.
![]() Ответ:
Ответ:![]()
12.
![]() Ответ:
Ответ:![]()
13.
![]() Ответ:
Ответ:![]()
![]() .
.
14.
![]() Ответ:
Ответ:![]()
15.
![]() Ответ:
Ответ:![]()
16.
![]() Ответ:
Ответ:![]()
17.
![]() Ответ:
Ответ:![]()
18.
 Ответ:
Ответ:![]()
19.![]()
Ответ:
![]()
20.
![]() Ответ:
Ответ:![]()
21.
![]() Ответ:
Ответ:![]()
22.
![]() Ответ:
Ответ:![]()
23.
![]() Ответ:
Ответ:![]()
24.
![]() Ответ:
Ответ:![]()
25.
![]() Ответ:
Ответ:![]()
Дифференциальные уравнения, приводимые к однородным задачи с решениями
1. (х+у
+2)dx+(2x+2y-1)dy=0
Ответ:![]() СR,
x+y+1=0.
СR,
x+y+1=0.
Решение:![]() a1=1,
b1=1,
a2=2,
b2=2;
a1=1,
b1=1,
a2=2,
b2=2;
![]() =
a1b2
- a2b1=
0.
=
a1b2
- a2b1=
0.
Так
как определитель
![]() =0,
то делаем заменуz=x+y,
=0,
то делаем заменуz=x+y,
![]()
![]()
![]()
![]() - (уравнения с разделяющимися переменными)
- (уравнения с разделяющимися переменными)![]()
![]() Возвратимся к исходным переменным:
Возвратимся к исходным переменным:![]()
2.
![]()
Решение:![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
3.
![]()
Решение:![]()
![]() Следовательно,
делаем замену x=u+x0
, y=V+y0
, где
Следовательно,
делаем замену x=u+x0
, y=V+y0
, где![]() определяются из системы
определяются из системы

![]() .
.
![]() (однородное
уравнение).
(однородное
уравнение).
![]()
![]()
![]() , C
, C![]() ,
t2-1
= 0
,
t2-1
= 0
![]() ,
C
,
C![]()
![]()
![]()
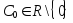 ,
,![]() ,
,![]()
Ответ:
![]()
4.![]() .
.
Решение:![]() ,a1 =
1 , b1
= 2 ,
,a1 =
1 , b1
= 2 ,
![]()
Замена:
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]() .
.
Проверка:
![]()
![]() ,
,![]() ,
,
![]() ;
;
![]() .
.
Ответ:
![]()
5.![]() .
.
Решение:![]() ,
,![]()

![]()
Замена:
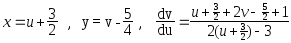 ,
,![]()
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
, ,
,![]()
Проверка:
![]() ,
,
![]() ,
,![]()
Ответ:
![]()
6.![]() ..
..
Решение:![]() ,
,
Замена:
![]() ;
;![]() ,
,![]()
![]() ,
,
![]()
![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
Ответ:
![]()
7.![]() .
.
Решение:![]()
Замена:
x + y = z
,
![]() ,
,![]() ,
,
![]()
![]()
![]()
Ответ:
![]()
8.![]() .
.
Решение:![]()
![]()

![]()
Замена:
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
Ответ:
![]()
![]()
Проверка:![]() ,
,