Лабораторная работа № 3

Изучение равноускоренного движения тел

на примере их свободного падения

в поле тяготения Земли

Цель работы: используя законы механики Ньютона, теоретически найти временную зависимость перемещения тела в поле тяготения Земли и экспериментально убедиться в справедливости полученных теоретических результатов.

Оборудование: установка, включающая штангу с закрепленными на ней электромагнитом и двумя фотодатчиками, стальной шарик, электронный миллисекундомер и миллиметровую линейку.

Продолжительность работы - 4 часа.

Теоретическая часть. Описание установки

Рассмотрим свободное падение тела массы в поле тяготения Земли вблизи ее поверхности. В этом случае в системе отсчета, связанной с Землей, на тело действует сила тяжести , которая включает силу тяготения , обусловленную гравитационным взаимодействием тела с Землей, и центробежную силу инерции , вызванную суточным вращением Земли, т.е. (рис.1). Следует отметить, что на тело, кроме указанных сил, действуют и другие силы, например, связанные с взаимодействием тела с Солнцем, Луной и другими космическими объектами, а также силы инерции, такие как сила инерции Кориолиса, зависящая от движения тела во вращающейся системе отсчета, и силы инерции, обусловленные вращением Земли вокруг Солнца. Однако в нашем случае эти силы по модулю значительно меньше сил и и поэтому не учитываются.

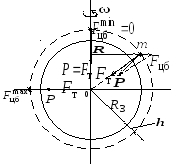
Рис.1. Силы, действующие на тело, в системе

отсчета, связанной с Землей

В соответствии с законом всемирного тяготения Ньютона силу притяжения можно записать в виде

(1)

где - гравитационная постоянная;  -  масса Земли; - радиус Земли;  - высота;  - единичный вектор ( ), направленный к центру массы Земли.

Выражение для центробежной силы инерции имеет вид:

, (2)

где - угловая скорость вращения Земли; - радиус-вектор, определяющий положение тела относительно оси вращения Земли.

В связи с малостью численного значения скорости вращения Земли ( ) центробежная сила инерции по модулю гораздо меньше силы притяжения ( ) и в нулевом приближении ею можно пренебречь. Тогда можно считать, что сила тяжести приблизительно равна силе притяжения ( ). Тот факт, что при решении нашей задачи можно не учитывать действие силы инерции, дает возможность считать систему отсчета, связанную с Землей, инерциальной. Это позволяет для описания движения использовать законы Ньютона.

Запишем в соответствии со вторым законом Ньютона уравнение движения тела:

, (3)

где  - ускорение тела.

Из (3) следует, что

. (4)

Будем рассматривать случай, когда тело находится на высоте над поверхностью Земли, много меньшей радиуса Земли ( ). Тогда (4) приближенно можно записать в виде

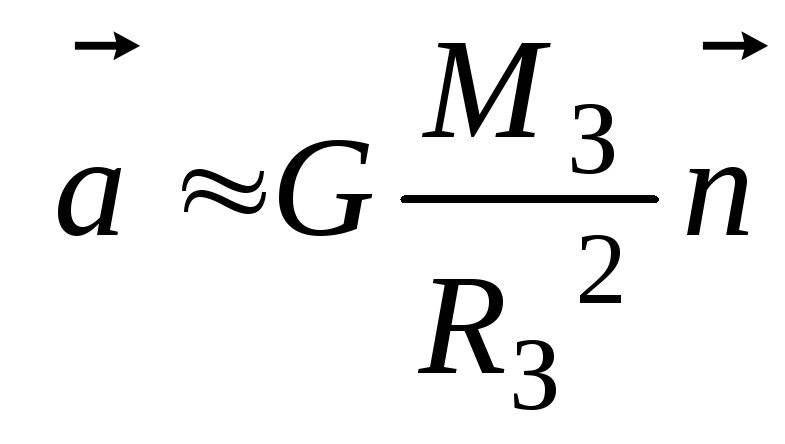. (5)

Величину обычно обозначают и называют ускорением свободного падения,

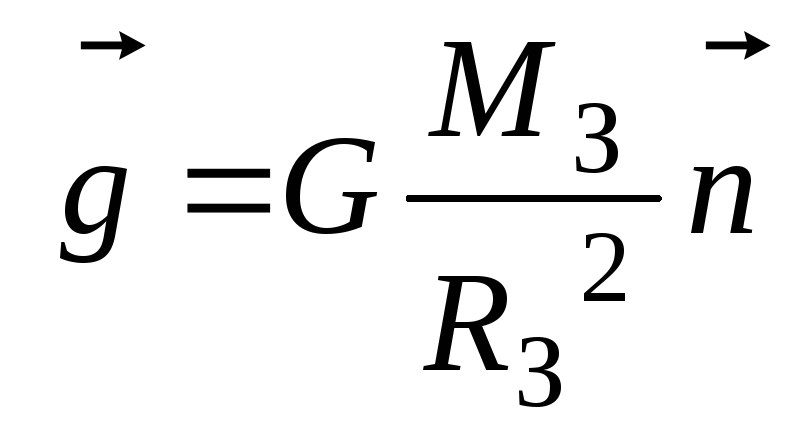. (6)

Анализ соотношений (5) и (6) показывает, что ускорение, с которым будет двигаться тело в поле тяготения Земли, равно ускорению свободного падения, а именно, .

Известно, что при равноускоренном движении модуль вектора ускорения и его направление в пространстве не должны изменяться в процессе движения. В нашем случае, строго говоря, это может иметь место только при движении тела вдоль радиальной прямой, проходящей через центр массы Земли.

Из (5) и (6) с учетом, что , где - скорость и - время, непосредственно следует

. (7)

0

0

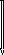
а

б

Рис.2. Схематическое изображение положения тела и его скорости в начальный момент времени и в момент времени t (а) и перемещение тела (б)

Проинтегрировав (7) с начальным условием (рис.2,а), получим:

. (8)

Приняв во внимание, что , где - элементарное перемещение, уравнение (8) преобразуем к виду

. (9)

Проинтегрировав (9) с учетом начального условия (рис.2,б), будем иметь:

, (10)

где и - векторы, характеризующие положение тела в начальный момент времени и в момент времени .

Разность векторов называется перемещением тела за время , которое в соответствии с (10) можно записать следующим образом:

. (11)

Векторы , и направлены вдоль оси . Следовательно, движение тела будет одномерным. В этом случае, спроектировав перемещение тела (11) на ось , получим:

. (12)

Отношение перемещения к промежутку времени , за который произошло это перемещение, определяет среднюю скорость тела:

. (13)

Анализ выражения (13) показывает, что средняя скорость линейно зависит от времени перемещения тела, причем удвоенное значение углового коэффициента прямой равно ускорению свободного падения, а значение свободного члена равно начальной скорости. Этот результат теоретического исследования может быть положен в основу экспериментального определения значений данных физических величин.

Механическая часть установки для экспериментального изучения движения тел в поле тяготения Земли схематично представлена на рис.3. Она состоит из массивного штатива 1, на котором с помощью кронштейнов крепятся электромагнит 3 и два фотодатчика 5. Электромагнит предназначен для удержания стального шарика 4, параметры движения которого при его свободном падении изучаются в данной работе. Для тонкой регулировки положения электромагнита, а следовательно и шарика, относительно верхнего фотодатчика служит винт 2. Кронштейны с фотодатчиками могут перемещаться по штанге штатива. Фиксация положения кронштейнов осуществляется винтами 6.

Измерение времени проводится с помощью электронного миллисекундомера, соединенного с двумя фотодатчиками и магнитом. При нажатии кнопки ″Пуск″ на передней панели миллисекундомера ток в цепи

электромагнита прерывается и шарик перестает удерживаться электромагнитом. При падении шарик пересекает лучи света, направленные на фотодатчики, при этом верхний фотодатчик включает миллисекундомер, а нижний фотодатчик его выключает. Таким образом измеряется время пролета шарика между фотодатчиками. Подготовка миллисекундомера к очередному измерению происходит при нажатии кнопки ″Сброс″.