Расчет пожарных рисков / Ocenka i raschet pozharnogo riska (NIIPPB) 2012

5.1.4. Термодинамические свойства среды

В качестве уравнения состояния используется модель идеального газа

ρ = PM

Динамическая вязкость смеси

N

μ = ∑Ymμm

m=1

(5.1.4.6)

Молярная масса смеси

5.2 Моделирование турбулентности

Считается, что при помощи уравнения Навье-Стокса можно описать как ламинарное, так и турбулентное течение (Ландау Л.Д., Лифшиц Е.М., 1986), практически же реальные достижения в расчетах турбулентных пото-

ков связаны с использованием полуэмпирических моделей турбулентности использующих подход Рейнольдса. Обоснованием необходимости примене-

ния такого подхода может служить приведенная в ряде работ оценка, соглас-

но которой отношение характерных размеров энергосодержащих (крупных)

вихрей и мелкомасштабных вихрей, определяющих «турбулентный фон»,

имеет порядок Re3/4. Естественно, что, ориентируясь на возможности совре-

менных ЭВМ, решить поставленные задачи в практически важном диапазоне

Re ³ 103 в настоящее время маловероятно.

Применим операцию осреднения по времени к уравнениям (5.1.1.1) и (5.1.1.2) получим уравнения движения в форме Рейнольдса (RANS):

где μt – турбулентная вязкость, k – кинетическая энергия турбулентных пульсаций.

Система уравнений (5.2.1)-(5.2.2) является не замкнутой, поэтому для

ее замыкания применяются различные полуэмпирические модели турбулент-

ности.

5.2.1 M-SST модель турбулентности.

Модель Ментера записывается путем суперпозиции моделей k-ε и k-ω,

основанной на том, что модели типа k-ε лучше описывают свойства свобод-

ных сдвиговых течений, модели k-ω имеют преимущество при моделирова-

нии пристеночных течений. Плавный переход от k-ω модели в пристеночной области к k-ε модели вдали от твердых стенок обеспечивается введением ве-

совой эмпирической функцией F1.

Вторая важная деталь модели состоит в изменении стандартной связи между k, ω и турбулентной вязкостью. Модификация этой связи состоит во введении перехода к формуле Бредшоу в пристеночной области. Согласно предположению Бредшоу напряжение сдвига в пограничном слое пропор-

ционально энергии турбулентных пульсаций.

Уравнения M-SST модели:

Транспортные уравнения для k и ω:

В члене генерации турбулентной энергии введен ограничитель:

Набор констант для свободных сдвиговых слоев:

Другие константы, использующиеся в модели:

β * = 0.09 κ = 0.41 a1 = 0.31

5.2.2 Метод пристеночных функций

Вблизи стенок турбулентный поток имеет сложную структуру со зна-

чительными градиентами. Во внутренней области, занимающей порядка 20%

толщины пограничного слоя, генерируется около 80% всей энергии турбу-

лентности. Для моделирования пристеночных течений часто применяется метод пристеночных функций, который позволяет экономить вычислитель-

ные ресурсы и учитывать влияния различных факторов (шероховатости стен-

ки, градиента давления вблизи стенки, вдув-отсос с поверхности тела) за счет введения эмпирической информации. Метод пристеночных функций, связы-

вающий параметры течения с расстоянием до стенки, представляет собой аналитическое решение упрощенных решений турбулентного течения.

В основе упрощения лежат следующие предположения:

1)локальное равновесие энергии турбулентных пульсаций (локальная скорость производства турбулентности уравновешивается скоростью вязкой диссипации);

2)постоянство касательного напряжения вдоль слоя;

3)пренебрежимо малый градиент давления вдоль потока;

4)локальная изотропность диссипирующих вихрей;

5) универсальность профиля скорости (слабая зависимость от числа Рейнольдса).

Следует отметить, что этот метод является в основном эмпирическим.

Метод пристеночных функций, основанный на обобщении эксперименталь-

ных данных для развитых турбулентных течений, достаточно хорошо описы-

вает пристеночные течения при значительных турбулентных числах Рей-

нольдса с пренебрежимо малой областью вязкого слоя. В случае не выполне-

ния гипотез, лежащих в основе пристеночных функций, требуется модифи-

кация соотношений метода или использование низкорейнольдсовых дисси-

пативных моделей.

5.3. Дискретизация

5.3.1. Сетки и контрольные объемы

Для решения заложенных в алгоритм пакета уравнений используется широко известный метод контрольного объема. Суть этого метода заключа-

ется в разбиении расчетной области на контрольные объемы и интегрирова-

нии исходных уравнений сохранения по каждому контрольному объему для получения конечно разностных соотношении.

Для возможности моделирования геометрически сложных объектов не-

обходимо использовать многоблочные неортогональные структурированные или неструктурированные сетки (Рис. 5.3.1).

158

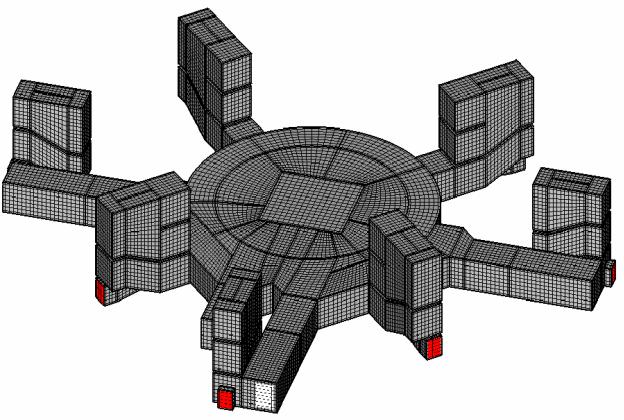
Рис. 5.3.1 Геометрия и расчетная сетка объекта защиты

5.3.2. Дискретизация обобщенного уравнения в декартовой систе-

ме координат

Любое дифференциальное уравнение сохранения можно представить в

виде обобщенного уравнения для соответствующей переменной Φ:

R

¶t

Задавая надлежащим образом Φ, Гф и источник SΦ, можно получить любое из упомянутых выше дифференциальных уравнений.

Запись уравнений в обобщенном виде удобна в том отношении, что ка-

кой-либо разработанный метод решения для этого уравнения может быть применен для многих уравнений подобной структуры, но различного физи-

ческого наполнения.

Дискретизация уравнения (5.3.2.1) будем производить методом кон-

трольного объема. Интегрируем уравнение (5.3.2.1) по контрольному объему.

R

¶t

Используя формулу Гаусса-Остроградского, переходим от объемных

интегралов к поверхностным и получаем:

где VolΦ -объем контрольного объема, SΦP -среднее в ячейке значение источни-

кового члена, I -суммарный конвективно-диффузионный поток через соот-

ветствующую грань контрольного объема.

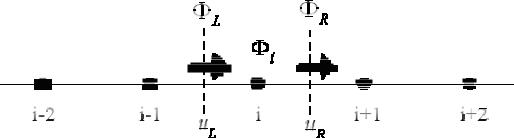
Описание расчетного алгоритма схем аппроксимации потока удобно проводить на одномерном шаблоне (например, в направлении оси OX), дис-

кретизация уравнения (5.3.2.1) в остальных направлениях осуществляется аналогично.

Рис. 5.3.2. Одномерный контрольный объем.

Величина суммарного потока для правой грани контрольного объема опреде-

ляется как:

160

здесь AR -площадь грани , ρR , uR , ΓR -значения плотности, скорости, коэффици-

ента диффузии на грани контрольного объема, которые находятся при помо-

щи интерполяции из соседних узлов

5.3.3. Аппроксимация диффузионного потока

Аппроксимация диффузионной части суммарного потока I произво-

дится при помощи центрально разностной схемы второго порядка точности.

5.3.4. Схемы аппроксимации конвективного потока

Задача нахождения конвективной части суммарного потока сводится к

отысканию значений искомой функции Φ на гранях контрольного объема по известным ее значениям в узлах сетки. Выбор способа интерполяции величи-

ны Φ между узлами расчетной сетки определяет свойства полученной при этом разностной схемы.

Гибридная схема сочетает противопоточную и центрально-разностную

дающее направление движения жидкости, гибридная схема вызывает боль-

шие вычислительные ошибки при нахождении локальных характеристик те-

чения.

Квадратичная противопоточная интерполяция (QUICK) была предло-

жена Леонардом [37].

Данная схема имеет второй порядок аппроксимации и обладает высо-

кой скоростью сходимости, чем и объясняется ее широкое применение при решении задач гидродинамики и тепломассообмена.

После публикации Колгана в 1972г. начало интенсивно развиваться новое поколение схем аппроксимации конвективного потока, которые полу-

чили названия TVD-схем (Total Variation Diminishing). Основным положи-

тельным свойством этих схем является монотонность получаемого решения,

которое достигается благодаря специальной методике расчета конвективных потоков через грани контрольного объема.

где Ψ(r) – функция-ограничитель, которая отвечает за свойства полученной

схемы. Функция-ограничитель Ψ(r) строится таким образом, чтобы давать

высокий порядок аппроксимации там, где это возможно, и в то же время га-

рантировать выполнение критерия ограниченности разностной схемы.

Предлагается использовать UMIST схему аппроксимации с ограниче-