Лабораторная работа №2

Сложение гармонических колебаний

Цель работы: Изучить биения и сложение двух взаимно перпендикулярных колебаний с помощью электронного осциллографа.

Оборудование и принадлежности: осциллограф универсальный С1-65, звуковой генератор, соединительные провода.

Контрольные вопросы:

1. Уравнение и график гармонических колебаний.

2. Что такое гармоническое колебание, его уравнение и график.

Колебания - движения или процессы, обладающие той или иной повторяемостью во времени. Простейшим типом колебаний являются гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса) и описываются уравнением типа

x = А соs (t + ₀),

где А – максимальное значение колеблющейся величины, называемое амплитудой колебания,  – круговая (циклическая) частота, ₀ или ₀ – начальная фаза колебания в момент t=0, (t + ₀) – фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до –1, то х может принимать значения от +А до –А.

Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемой периодом колебания, за который фаза колебания получает приращение 2.

Т= 2

Величина, обратная периоду колебаний,  = 1/Т называется частотой колебаний и равна числу полных колебаний, совершаемых в единицу времени. Откуда =2. Единица частоты  - герц (Гц). 1 Гц – частота периодического процесса, при которой за 1 с совершается 1 цикл процесса.

Г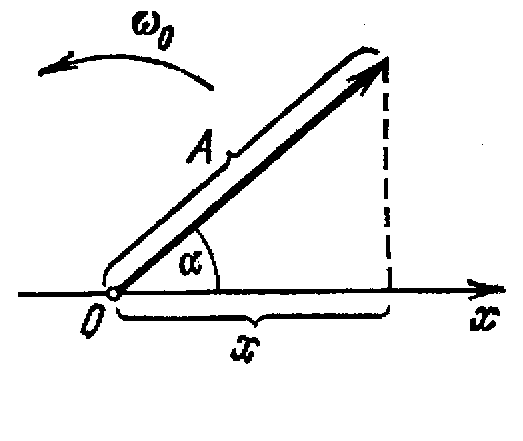армонические колебания могут изображаться графически методом вращающегося вектора амплитуды, или методом векторных диаграмм.

Возьмем ось, вдоль которой будем откладывать колеблющуюся величину x (рис.1). Из взятой на оси точки О отложим вектор длины A, образующий с осью угол . Если привести этот вектор во вращение с угло­вой скоростью ω, то проекция конца вектора будет перемещать­ся по оси x в пределах от -А до +A, причем координата этой проекции будет изменяться со временем по закону

Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с ам­плитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с на­чальной фазой, равной углу, образуемому вектором с осью в начальный момент времени.

Таким образом, гармоническое колебание может быть задано с помощью вектора, длина которого рав­на амплитуде колебания, а направление образует с осью x угол, равный начальной фазе колебаний.

Представление гармонических колебаний с помощью векторов позволяет заменить сложение функций сложением векторов, что значительно проще.

3. При каких условиях наблюдаются биения?

Рассмотрим сложение двух гармонических колебаний, происходящих вдоль одной прямой с частотами ω₁ и ω₂, незначительно отличающихся друг от друга. (Ω=( |ω₁ - ω₂ |<< ω₁ и Ω<< ω₂ ).Пусть в начальный момент времени фазы складываемых колебаний одинаковы. Тогда эти колебания запишутся в виде

и (4)

Найдем сумму двух таких колебаний, предположив для простоты сначала, что их амплитуды одинаковы (A₁ = A₂): Отсюда видно, что результирующее колебание (биение) происходит с частотой (ω₁+ω₂)/2, а амплитуда колебаний со временем изменяется в пределах от 2A₁ до 0 по закону (рис. 3). Значение 2A₁ достигается тогда, когда фазы складываемых колебаний совпадают, а нуль - когда фазы противоположны. Периодическое изменение результирующей амплитуды, получающееся при сложении колебаний, совершающихся с близкими частотами и вдоль одной прямой, называют биениями. Циклическая частота биений Ω= |ω₁ - ω₂ |, период биений Т = 2π/ Ω (рис.3) и частота биений

ν_б = 1/T_б = |ν₁ - ν₂ |, где ν₁ и ν₂- частоты складываемых колебаний.

Если амплитуды складываемых колебаний не равны (A₁ # A₂), то максимальное значение амплитуды результирующего колебания равно A₁+A₂, а минимальное  А₁-А₂. В этом случае биения выражены менее четко (рис.4). Частоты Ω, ν_б и период T_б определяются разностью частот складываемых колебаний и не зависят от их амплитуд и начальных фаз.

Сложение колебаний во взаимно перпендикулярных направлениях.

Представим две взаимно перпен­дикулярные векторные величины x и y, изменяющие­ся со временем с одинаковой частотой ω по гармони­ческому закону

(6) где e_x и e_у — орты координатных осей x и y, А и B — амплитуды колебаний. Величинами x и у может быть, например, смещения материальной точки (частицы) из положения равновесия. В случае колеблющейся частицы величины

, , (7)

определяют координаты частицы на плоскости xy. Частица будет двигаться по некоторой траектории, вид которой зависит от раз­ности фаз обоих колебаний. Выражения (6) пред­ставляют собой заданное в параметрической форме уравнение этой траектории. Чтобы получить уравне­ние траектории в обычном виде, нужно исключить из уравнений (6) параметр t. Из первого уравне­ния следует, что

(8)

Соответственно (9)

Развернем косинус во втором из уравнений (6) по формуле для косинуса суммы:

Подставим вместо cosωt и sinωt их значения (3) и (4):

Преобразуем это уравнение

(10)

Это уравнение эллипса, оси которого по­вернуты относительно координатных осей х и у. Ори­ентация эллипса и его полуоси зависят довольно сложным образом от амплитуд A и В и разности фаз α.

Попробуем найти форму траектории для нескольких частных случаев.

1. Разность фаз α равна нулю.

В этом случае уравнение (10) упрощается следующим образом:(11)

Отсюда получается уравнение прямой:

Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой ω и ам­плитудой, равной (рис. 5а).