
- •Линейные стабилизаторы напряжения. Параметрический стабилизатор.
- •Линейные стабилизаторы напряжения. Компенсационный стабилизатор.
- •Линейные стабилизаторы напряжения. Интегральные стабилизаторы.
- •Импульсные источники напряжения. Повышающий преобразователь.
- •Импульсные источники напряжения. Понижающий преобразователь.
- •Импульсные источники напряжения. Инвертор.
- •Импульсные преобразователи с гальванической развязкой. Однотактные.
- •Импульсные преобразователи с гальванической развязкой. Двухтактные.
- •Расчеты тепловыделения схем источников питания.
- •Операционный усилитель. Назначение. Параметры.
- •Операционный усилитель. Основные схемы включения.
- •Операционный усилитель. Реализация источника тока.
- •Влияние емкостной нагрузки на работу оу, схемы компенсации.
- •Схемы сложения и вычитания на оу.
- •Интегрирующее и дифференцирующее звенья на оу.
- •Вычисление логарифма и экспоненты на оу.
- •Активные фильтры. Разновидности по виду ачх, основные характеристики.
- •Представление передаточной функции фильтра. Реализация фильтров высоких порядков.
- •Реализация звеньев фнч и фвч первого и второго порядка.
- •Преобразование нормированного фнч в фнч и фвч с заданной частотой среза.
- •Преобразование нормированного фнч в полосовые и режекторные фильтры.
- •Усилители мощности. Классы а, в.
- •Усилители мощности. Классы ab, d.
-
Преобразование нормированного фнч в полосовые и режекторные фильтры.
Преобразование ФНЧ - ПФ
Коридор
АЧХ для Полосового Фильтра(ПФ). 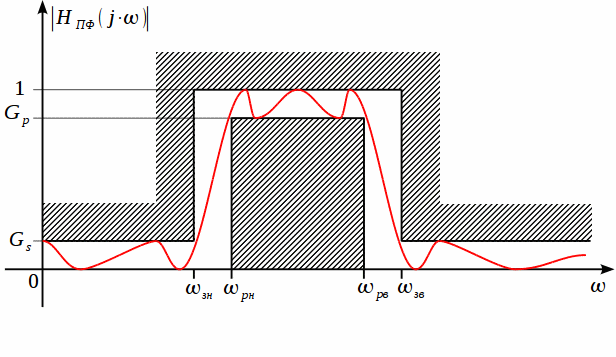
Преобразование нормированного ФНЧ в полосовой фильтр выполняется в виде постановки:
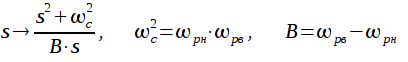
При этом частотная ось нормированного ФНЧ связана с частотной осью ПФ соотношением:

Обратите
внимание, что при пересчете используются
как положительные, так и отрицательные
частоты
 .
Также можно заметить, если
.
Также можно заметить, если
 , то
, то
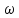 =
=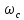 ,
т.е. нулевая частота исходного
нормированного ФНЧ преобразуется в
частоту
,
т.е. нулевая частота исходного
нормированного ФНЧ преобразуется в
частоту
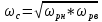 . Если
. Если
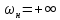 ,
то
,
то
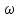 =
=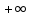 ,
а если
,
а если
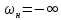 ,
то
,
то
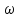 =
= . Таким образом, вся отрицательная
полуось частот нормированного ФНЧ
преобразуется в интервал от 0 до
. Таким образом, вся отрицательная
полуось частот нормированного ФНЧ
преобразуется в интервал от 0 до
 полосового фильтра, а положительная
полуось частот нормированного ФНЧ
преобразуется в интервал от
полосового фильтра, а положительная
полуось частот нормированного ФНЧ
преобразуется в интервал от
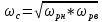 до бесконечности. Графически частотное
преобразование ФНЧ-ПФ показано на
рисунке.
до бесконечности. Графически частотное
преобразование ФНЧ-ПФ показано на
рисунке.

На
верхнем левом графике показана АЧХ
исходного нормированного ФНЧ
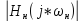 для положительных и отрицательных
частот
для положительных и отрицательных
частот
 (поскольку коэффициенты передаточной
функции нормированного ФНЧ чисто
вещественны, то
(поскольку коэффициенты передаточной
функции нормированного ФНЧ чисто
вещественны, то
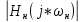 симметрично относительно нуля). Поскольку
требуется оставить без изменения уровни
подавления в полосе заграждения и
неравномерность в полосе пропускания
пересчитанного фильтра, то используется
проекция
симметрично относительно нуля). Поскольку
требуется оставить без изменения уровни
подавления в полосе заграждения и
неравномерность в полосе пропускания
пересчитанного фильтра, то используется
проекция
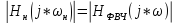 (верхний
правый график, проекции отображены
синей пунктирной линией). Преобразование
частоты согласно соотношению частоты
оси ФНЧ и частоты оси ПФ показано на
нижнем левом графике (линии проекции
отображены зеленой пунктирной линией).
На правом нижнем графике показана АЧХ
пересчитанного ПФ, повернутая на 90
градусов, полученная в результате
пересечения линий проекции.
(верхний
правый график, проекции отображены
синей пунктирной линией). Преобразование
частоты согласно соотношению частоты
оси ФНЧ и частоты оси ПФ показано на
нижнем левом графике (линии проекции
отображены зеленой пунктирной линией).
На правом нижнем графике показана АЧХ
пересчитанного ПФ, повернутая на 90
градусов, полученная в результате
пересечения линий проекции.
Сделаем
важное замечание. Если некоторая частота
 преобразуется согласно соотношению*
в частоту
преобразуется согласно соотношению*
в частоту
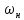 , а частота
, а частота
 в частоту
в частоту
 , то можно записать:
, то можно записать:
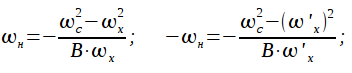
Откуда:
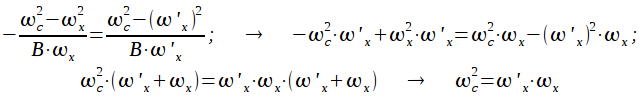
Таким
образом мы получили, что симметричные
относительно
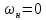 точки АЧХ исходного нормированного
ФНЧ преобразуются в точки с геометрической
симметрией относительно частоты
точки АЧХ исходного нормированного
ФНЧ преобразуются в точки с геометрической
симметрией относительно частоты
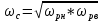 (термин геометрическая симметрия
означает, что
(термин геометрическая симметрия
означает, что
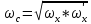 , т.е. есть среднее геометрическое
, т.е. есть среднее геометрическое
 и
и
 ). Это крайне важное свойство частотного
преобразования ФНЧ-ПФ.
). Это крайне важное свойство частотного
преобразования ФНЧ-ПФ.
Расчёт
полосового фильтра по заданному коридору
АЧХ.![]()
Мы
произвольно задали , рассчитали
частоту
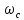 согласно выражению
согласно выражению
 .
Теперь воспользовавшись правилом
геометрической симметрии мы можем
проверить куда относительно нижней
частоты заграждения
.
Теперь воспользовавшись правилом
геометрической симметрии мы можем
проверить куда относительно нижней
частоты заграждения
 попадает частота
попадает частота
 симметричная верхней частоты заграждения
симметричная верхней частоты заграждения
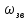 :
:

Частоту заграждения нормированного ФНЧ, можно рассчитать из выражения:
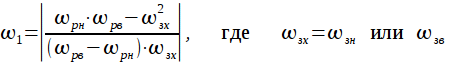
Преобразование ФНЧ – РФ
Как
и полосовой фильтр, РФ имеет две переходные
полосы, причем в отличии от ПФ, частоты
коридора АЧХ режекторного фильтра
удовлетворяют следующему правилу:
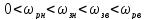 , т.е. верхняя и нижняя частоты заграждения
находятся рядом, а верхняя и нижняя
частоты пропускания по краям.
, т.е. верхняя и нижняя частоты заграждения
находятся рядом, а верхняя и нижняя
частоты пропускания по краям.
АЧХ
Режектороного Фильтра(РФ).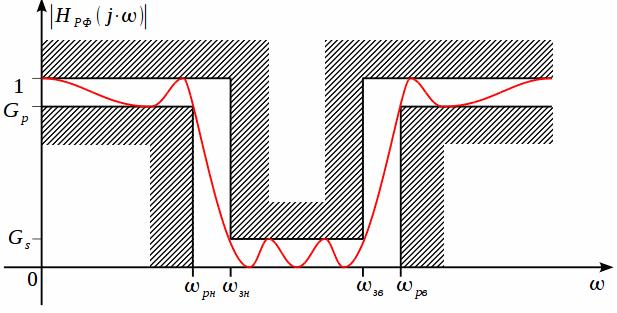
Преобразования фильтра нижних частот в режекторный фильтр осуществляется при помощи подстановки:
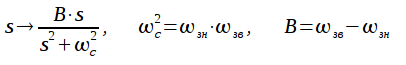
Видно что данная подстановка обратна преобразованию ФНЧ-ПФ. При этом частотная ось ФНЧ связана с частотной осью РФ соотношением:
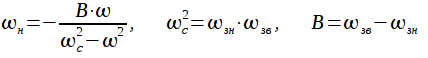
Обратите
внимание, что при пересчете используются
как положительные, так и отрицательные
частоты
 .
Также можно заметить, если
.
Также можно заметить, если
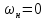 , то
, то
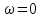 ,
или
,
или
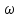 =
=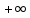 ,
т.е. нулевая частота исходного ФНЧ
«расходится» на 0 и на бесконечность.
Если
,
т.е. нулевая частота исходного ФНЧ
«расходится» на 0 и на бесконечность.
Если
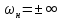 ,
то
,
то
 . Таким образом, вся отрицательная
полуось частот исходного ФНЧ преобразуется
в интервал от 0 до
. Таким образом, вся отрицательная
полуось частот исходного ФНЧ преобразуется
в интервал от 0 до
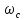 режекторного фильтра, а положительная
полуось частот нормированного ФНЧ
преобразуется в интервал от
режекторного фильтра, а положительная
полуось частот нормированного ФНЧ
преобразуется в интервал от
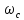 до бесконечности. При этом полуоси
исходного ФНЧ как бы «выворачиваются»,
т.е. нулевая частота
до бесконечности. При этом полуоси
исходного ФНЧ как бы «выворачиваются»,
т.е. нулевая частота
 «раздваивается» и расходится на
бесконечность
«раздваивается» и расходится на
бесконечность
 и
и
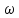 =
= ,
а
частоты разнесенные на бесконечность
,
а
частоты разнесенные на бесконечность
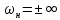 ,
сходятся в точке
,
сходятся в точке
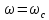 .
Графически частотное преобразование
ФНЧ-РФ показано на рисунке.
.
Графически частотное преобразование
ФНЧ-РФ показано на рисунке.
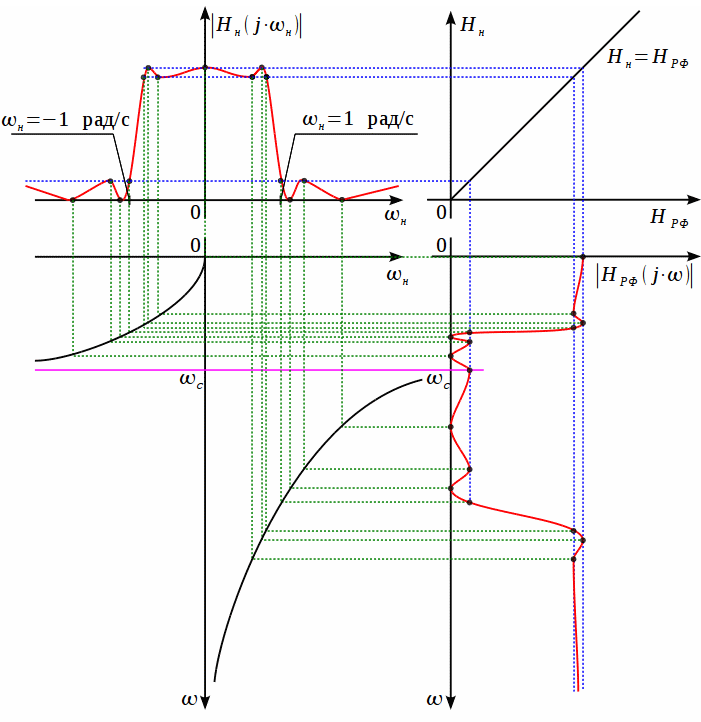
Как
и в случае с полосовым фильтром, частотная
характеристика преобразованного
режекторного фильтра обладает
геометрической симметрией относительно
частоты
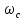 .
Действительно, возьмем две произвольные
частоты, расположенные симметрично
относительно нуля в АЧХ исходного ФНЧ
.
Действительно, возьмем две произвольные
частоты, расположенные симметрично
относительно нуля в АЧХ исходного ФНЧ
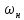 и
и
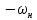 , тогда этим частотам после преобразования
будут соответствовать некоторые частоты
режекторного фильтра:
, тогда этим частотам после преобразования
будут соответствовать некоторые частоты
режекторного фильтра:
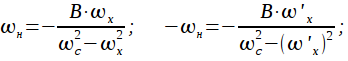
Тогда можно приравнять:

Для
задания частоты среза
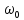 исходного ФНЧ необходимо, произвести
анализ по аналогии с тем, что мы делали
при расчете ПФ. А именно рассчитаем
симметричные частоты для верхней и
нижней частот среза РФ:
исходного ФНЧ необходимо, произвести
анализ по аналогии с тем, что мы делали
при расчете ПФ. А именно рассчитаем
симметричные частоты для верхней и
нижней частот среза РФ:

После
этого необходимо сделать выбор: если
 , тогда пересчет частоты среза исходного
ФНЧ осуществлять на основе верхней
частоты среза по формуле:
, тогда пересчет частоты среза исходного
ФНЧ осуществлять на основе верхней
частоты среза по формуле:

В
противном случае (если
 ),
то пересчет осуществлять по нижней
частоте среза РФ:
),
то пересчет осуществлять по нижней
частоте среза РФ:

Сформируем следующий алгоритм:
-
Выбор переходной полосы, по которой производить пересчет коридора АЧХ для ФНЧ по рассмотренному выше правилу и расчет частоты среза ФНЧ
-
Расчет ФНЧ по заданному коридору АЧХ, полученному в шаге 1. Параметры неравномерности в полосе пропускания и уровня подавления в полосе заграждения принимаются такие же что и у режекторного фильтра.
-
При помощи частотного преобразования производим пересчет частотной характеристики ФНЧ в РФ
