1 семестр / Fizika_2

МАГНЕТИЗМ

Закон Ампера определяет силу, действующую на проводник с током, помещенный в магнитное поле:

 

; ,

 

где – сила тока; – элемент длины провода (вектор совпадает по направлению с током ); – длина проводника. Сила Ампера перпендикулярна направлению тока и направлению вектора магнитной индукции.

Если прямолинейный проводник длиной находится в однородном поле, то модуль силы Ампера определяется выражением (рис. 3.7):

.

 

 

Рис. 3.7. Правило левой руки и правило буравчика для определения направления силы Ампера

 

Сила Лоренца (полная электромагнитная сила, действующая на заряженную частицу в электрическом и магнитном полях)

 

,

 

где – электрический заряд; – напряженность электрического поля; – скорость частицы; – индукция магнитного поля.

Только в магнитном поле на движущуюся заряженную частицу действует магнитная составляющая силы Лоренца (рис. 3.8)

 

.

 

Магнитная составляющая силы Лоренца перпендикулярна вектору скорости и вектору магнитной индукции. Она не изменяет величины скорости, а изменяет только ее направление, следовательно, работы не совершает.

Рис. 3.8. Сила Лоренца

 

Если частица влетает в магнитное поле под углом к силовым линиям , то она равномерно движется в магнитном поле по окружности радиусом и периодом обращения:

; ,

 

где – масса частицы.

Если заряженная частица влетает в однородное магнитное поле под углом , то она движется по винтовой линии (рис. 3.9).

 

 

Рис. 3.9. Движение по винтовой линии заряженной частицы в магнитном поле

 

 

Рис. 3.10. Заряженные частицы не выходят за пределы магнитной «бутылки». Поле может быть создано с помощью двух круглых витков с током

 

Отношение магнитного момента к механическому L (моменту импульса) заряженной частицы, движущейся по круговой орбите,

,

 

где ‑ заряд частицы; т ‑ масса частицы.

Вектор магнитной индукции(В)- это основная силовая характеристика магнитного поля (обозначается В). Пробный контур, помещенный в магнитное поле, испытывает со стороны магнитного поля действие вращающего момента сил М.

Бесконечно длинный ток величины I создает на расстоянии r от себя магнитное поле:

где Мо - магнитная постоянная, R - расстояние, I - сила тока в проводнике.

Магнитная индукция - это векторная физическая величина, являющаяся силовой характеристикой в данной точке магнитного поля.

 

Единица магнитной индукции - тесла (Тл).

Магни́тная инду́кция — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

В вакууме B = μ₀H.

Более конкретно, — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля на заряд , движущийся со скоростью , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).

 

Вектор магнитной индукции (В) – аналог напряженности электрического поля. Основной силовой характеристикой маг­нитного поля является вектор магнитной индукции.

Опытным путем было установлено, что для одной и той же точки магнитного поля максимальный вращающий момент М (момент сил) пропорционален произведению силы тока I в контуре на его площадь S. Величину IS называют магнитным моментом контура Pm.

Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения^[1]; магнитная составляющая электромагнитного поля^[2].

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, что обычно проявляется в существенно меньшей степени) (постоянные магниты).

Магнитное поле создается движущимися заряженными частицами, поэтому магнитное поле всегда есть вокруг проводников с током.

Напряженность магнитного поля – величина, характеризующая интенсивность магнитного поля вокруг проводника без учета магнитных свойств среды, в которой находятся проводники с током. Напряженность магнитного поля зависит только от силы тока в проводнике и расстояния до проводника. Чем дальше от проводника, тем меньше напряженность магнитного поля, созданного этим проводником.

Рис. 2.1

Магнитная индукция (В) – характеризует величину и направление магнитного поля с учетом магнитных свойств среды. Вектор магнитной индукции в любой точке поля изображается по касательной к линии магнитного поля (рис. 2.1). Единица измерения магнитной индукции – Тесла (Т).

 

В = Н× μ₀ ×μ, где μ₀ – магнитная постоянная,

μ – магнитная проницаемость.

Магнитная проницаемость (μ) – характеризует магнитные свойства различных материалов. Это безразмерная величина, показывающая во сколько раз в данной среде магнитное поле сильнее, чем в вакууме. Для воздуха μ = 1. (большую магнитную проницаемость имеют только ферромагнитные материалы – железо, никель, кобальт и их сплавы).

Магнитная постоянная μ₀ = 4π × 10^-7 – магнитная проницаемость вакуума.

 

Направление линий магнитного поля определяется по правилу буравчика.

Правило буравчика - если поступательное движение буравчика совпадает с направлением тока, то направление вращения его рукоятки указывает направление магнитных линий (рис. 2.2).

Рис. 2.2 Правило буравчика Рис. 2.3 Правило левой руки Рис. 2.4 Правило правой руки

На проводник с током, расположенный в магнитном поле, действует электромагнитная сила (F), направление которой определяется по правилу левой руки.

Правило левой руки (рис. 2.3): если ладонь левой руки расположена так, что вектор магнитной индукции вхо­дит в нее, вытянутые четыре пальца совпадают с направлением тока, то отогнутый под прямым углом большой палец левой руки указывает направление электромагнитной силы,которая стремится переместить проводник.

 

Электро­магнитная сила определяется по формуле: F = B× I×l

 

где В – магнитная индукция, Т;

I – сила тока, протекающего по проводнику, А;

l – длина проводника, м;

 

Проводник, движущийся в магнитном поле, можно рассматривать как простейший электродвигатель.

Электромагнитная индукция – явление возникновение электродвижущей силы (ЭДС) на концах проводника, движущегося в магнитном поле (то есть механическая энергия движения проводника превращается в электрическую энергию). Наведенная ЭДС называется индуктированной ЭДС. Направление индуктированной ЭДС определяется по правилу правой руки.

Правило правой руки (рис. 2.4): ладонь правой руки располагают так, чтобы магнитные линии входили в нее, отогнутый под прямым углом большой палец совмещают с направлением движения проводника, тогда вытянутые четыре пальца укажут направление индуктированной ЭДС.

 

Движущийся под действием механической силы в магнитном поле провод можно рассматривать как простейший электрический генератор.

В 1820 г. Био и Савар исследовали магнитные поля, создаваемые токами, текущими по тонким проводам различной формы. Путем анализа этих экспериментальных данных Лаплас установил закон, получивший название закона Био-Савара-Лапласа:

1) Магнитное поле любого тока может быть найдено как векторная сумма полей, создаваемых отдельными элементарными участками тока. Каждый элемент тока характеризуется величиной , где - сила тока, текущего в этом элементе, - длина элемента тока, а вектор указывает направление тока.

2) Для магнитной индукции поля, создаваемого элементом тока Лаплас получил выражение

(6.4)

 

где - радиус-вектор, проведенный из точки расположения элемента тока в точку наблюдения, где определяется индукция , (см. рис. 6.3), - коэффициент пропорциональности, зависящий от выбора единиц измерения и магнитных свойств среды, где протекает ток; в системе СИ для вакуума

 

 

где - магнитная проницаемость вакуума, измеряемая в .

Модуль выражения (6.4) равен

 

(6.5)

 

где - угол между векторами и .

Рис. 6.3. К формулировке закона Био-Савара-Лапласа

Применим формулу (6.5) для вычисления магнитного поля, создаваемого током, текущим по тонкому прямолинейному проводу теоретически бесконечной длины (см. рис. 6.4).

 

Рис. 6.4.

 

Векторы от всех элементов тока прямолинейного провода в точке наблюдения направлены одинаково – за плоскость чертежа. Точка наблюдения находится на расстоянии от провода. Согласно рис. 6.4,

 

 

Эти выражения подставим в (6.5):

 

 

При движении вдоль провода угол изменяется в пределах от до . Поэтому

(6.6)

 

Линии индукции магнитного поля - касательные к вектору индукции в каждой точке. Для прямолинейного провода с током эти линии представляют собой концентрические окружности, охватывающие провод, как показано на рис. 6.5. Плоскости окружностей перпендикулярны к проводу.

 

Рис. 6.5. Линии индукции магнитного поля

прямолинейного провода с током

 

Направление обхода линий индукции задается вектором индукции магнитного поля. Это направление связано с направлением тока в проводе по правилу правого винта, как видно из рис. 6.5.

Применение принципа суперпозиции и формулы (6.4) позволяет найти индукцию магнитного поля, создаваемого постоянным током силой , который течет по замкнутому контуру :

 

(6.7)

 

где - радиус-вектор, проведенный от элемента тока к точке наблюдения, где вычисляется вектор .

Формула (6.7) применима для линейного тока. Пусть постоянный ток распределен в объеме с плотностью . Переход от линейного тока к объемному току поясняет рис. 6.6, где показан элемент тонкого проводника длиной и поперечным сечением .

Рис. 6.6.

Объем элемента равен . Связь силы тока с плотностью тока в проводнике дается формулой , откуда , или в векторном виде

(6.8)

 

С учетом (6.8) из (6.7) выражаем индукцию магнитного поля, созданного объемными токами, распределенными в объеме как

 

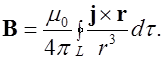(6.9)

Теорема Гаусса для поля В: поток век­тора магнитной индукции через любую замкнутую поверхность равен нулю:

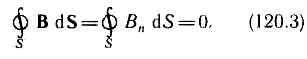
Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

Результирующая сила, действующая на контур, равна интегралу по контуру с током , т.е.

.

Рассмотрим однородное магнитное поле.

,

, а

,

т.е. результирующая сила Ампера равна нулю.

В неоднородном магнитном поле в общем случае

.

Рассмотрим элементарный контур (плоский контур, размеры которого малы). Введем

,

где дипольный магнитный момент,

(или просто магнитный момент); аналогичен моменту, действующему в электрическом поле на диполь, .

Магни́тный моме́нт, магни́тный дипо́льный моме́нт — основная величина, характеризующая магнитные свойства вещества (источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки; элементарным источником магнетизма считают замкнутый ток).

А^.м².

Здесь - площадь, ограниченная контуром;

- нормаль к контуру, направление которой связано с направлением тока по правилу правого винта (рис.49).

Cила, действующая на такой контур в неоднородном магнитном поле,

.

эта формула записана с учетом малости контура,

(приводится без вывода).

Это выражение аналогично выражению для силы, действующей на электрический диполь в электрическом поле

.

В проекции на некоторую ось :

.

В однородном поле

(т.к. ).

Сила не совпадает по направлению с вектором и вектором , а совпадает с направлением производной вектора по направлению вектора , или вектора , в месте расположения контура.

Например, для прямого тока - см. рис. 50, 51.

Определим момент сил. Рассмотрим однородное поле.

суммарный момент не зависит от точки, относительно которой определяется момент сил, и

- по определению;

для контура произвольной формы

. (*)

- для плоского контура,

- в общем случае.

Из (*) и свойств векторного произведения

и ;

.

- устойчивое положение контура,

- неустойчивое положение контура (при отклонении возникает момент сил, стремящийся еще более отклонить контур).

Формула (*) используется и для неоднородных магнитных полей при малых размерах контура (когда влиянием неоднородности на момент можно пренебречь, - см., например, элементарный контур).

Элементарный контур в неоднородном магнитном поле (как и электрический диполь во внешнем неоднородном электрическом поле)

1) поворачивается к положению устойчивого равновесия ;

2) под действием контур втягивается в область, где больше.

Магнитный диполь — аналог электрического, который можно представить себе как систему двух «магнитных зарядов» (эта аналогия условна, так как магнитных зарядов, с точки зрения современной электродинамики, не существует). В качестве модели магнитного диполя можно рассматривать небольшую (по сравнению с расстояниями, на которых излучается генерируемое диполем магнитное поле) плоскую замкнутую проводящую рамку площади по которой течёт ток При этом магнитным моментом диполя (в системе СГСМ) называют величину где  — единичный вектор, направленный перпендикулярно плоскости рамки в том направлении, при наблюдении в котором ток в рамке представляется текущим по часовой стрелке.

Выражения для вращающего момента , действующего со стороны магнитного поля на магнитный диполь, и потенциальной энергии постоянного магнитного диполя в магнитном поле, аналогичны соответствующим формулам для взаимодействия электрического диполя с электрическим полем, только входят туда магнитный момент и вектор магнитной индукции :

а) Результирующая сила F, действующая на диполь со стороны внешнего электрического поля E, создаваемого сторонними зарядами, равна векторной сумме сил, действующих на отдельные заряды диполя, и равна:

,

где E₊ и E_– – вектора напряженности электрических полей в т. нахождения положительного q₊ и отрицательного q_– зарядов диполя, соответственно, а

ΔE = (E₊ – E_–) – есть приращение поля E на длине l (расстояние между зарядами диполя) вдоль направления вектора P электрического момента диполя (от q_– к q₊).

Т. к. расстояние l между зарядами диполя мало, то ΔE = (E₊ – E_–) = ΔE*l/l = (мы ΔE помножили и разделили на малое значение l, эквивалентное Δl и отношение ΔE/Δl при Δl → 0 заменили на частную производную (поля E по направлению l )) и тогда