Признак Даламбера

Конечная форма признака Даламбера.

Пусть 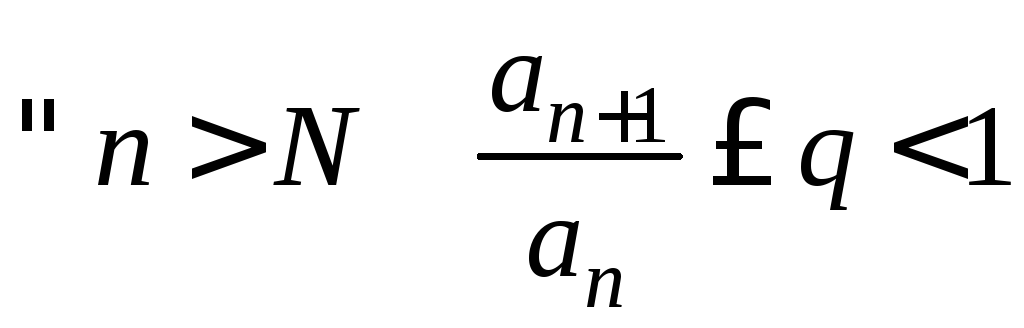, тогда рядсходится.

Пусть 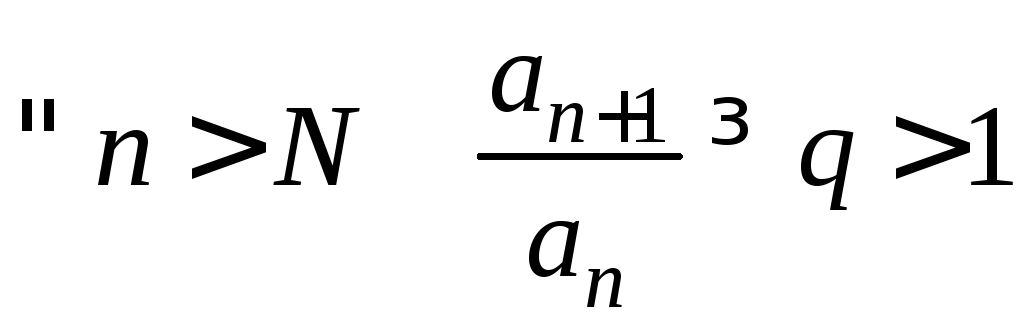, тогда рядрасходится.

Доказательство. Пусть .

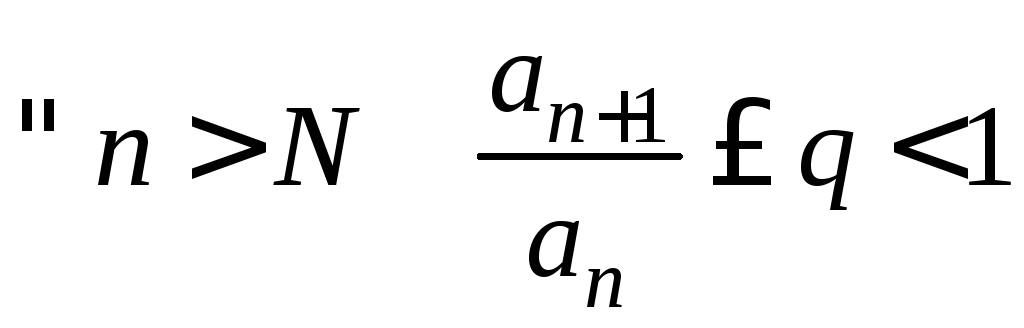Тогда .

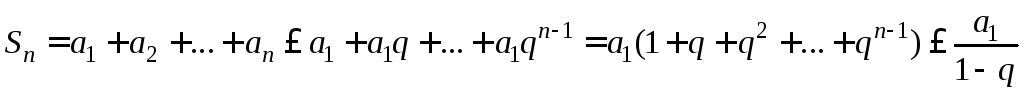, и ряд сходится.

Пусть 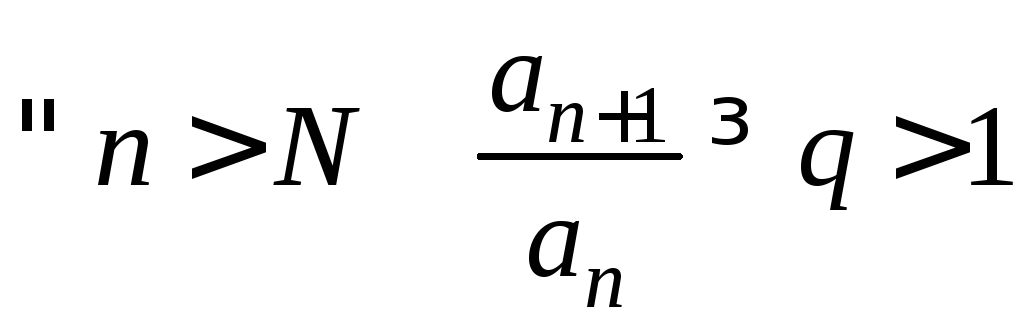, Тогда . Поэтомуне стремится к нулю при, необходимый признак сходимости ряда не выполнен, рядрасходится.

Предельная форма признака Даламбера.

Пусть , тогда рядсходится. Пусть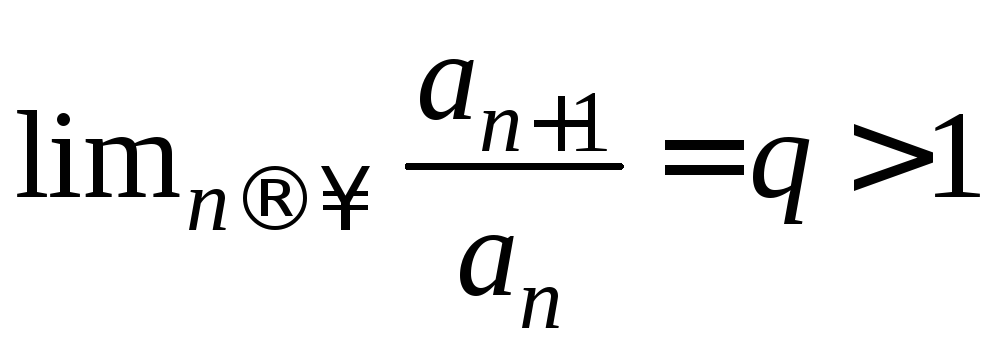, тогда рядрасходится. Если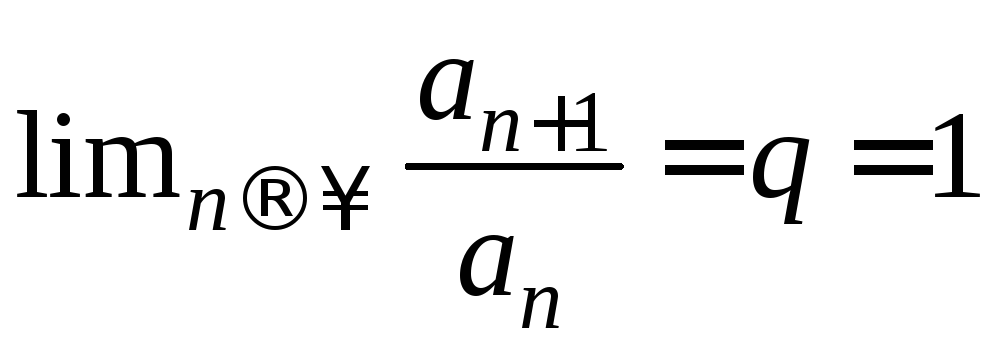, то признак не позволяет сделать вывод о сходимости или расходимости ряда.

Доказательство. Пусть 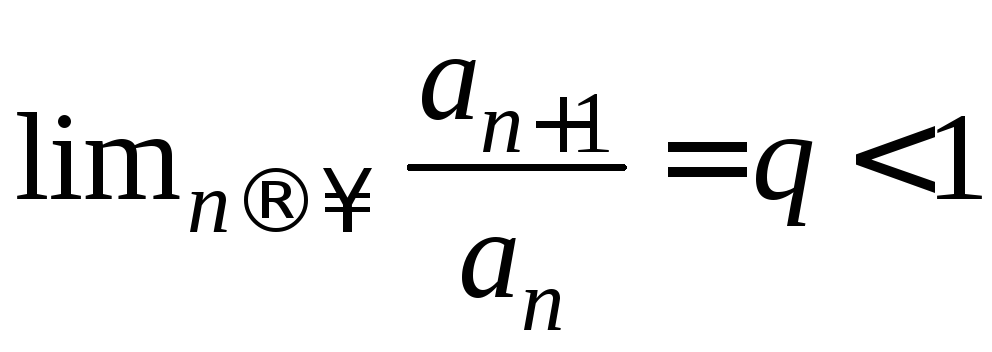. Тогда.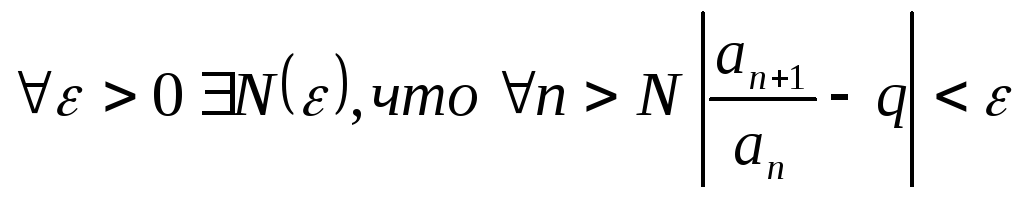

При малом . По конечной форме признака Даламбера рядсходится.

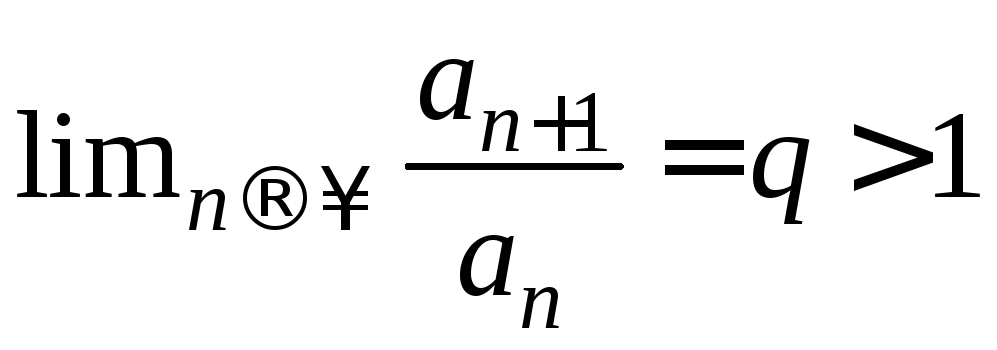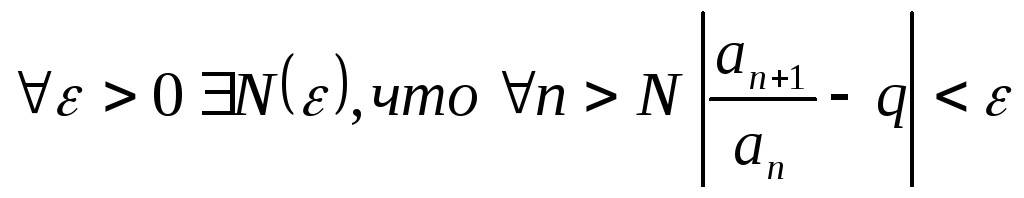Пусть . Тогда. При малом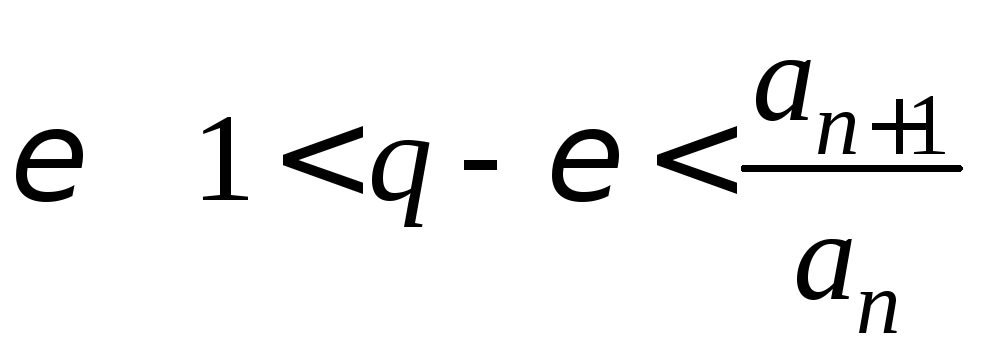, то есть. Поэтомуне стремится к нулю при, необходимый признак сходимости ряда не выполнен, рядрасходится.

Замечание. Признак Даламбера удобно применять, когда общий член ряда содержит произведение некоторых чисел или факториал.

Правда, если общий член ряда содержит факториал, то его можно заменить по формуле Стирлинга 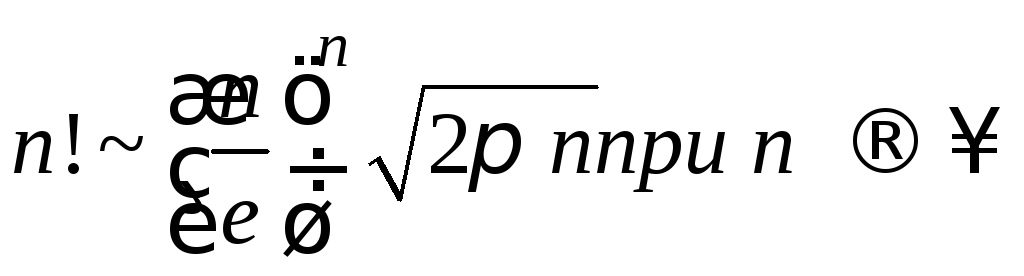и применять второй признак сравнения.

Пример. .

.

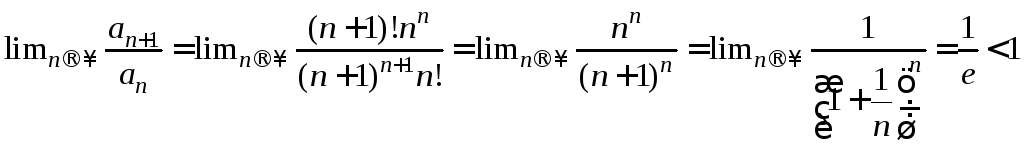Ряд сходится по признаку Даламбера.

Пример. .

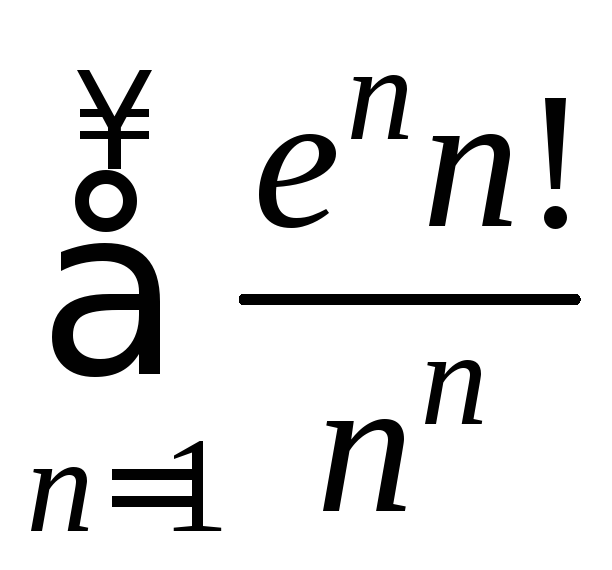Рассмотрим 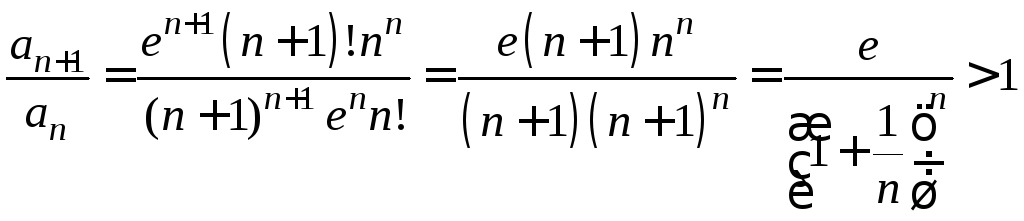, так как последовательность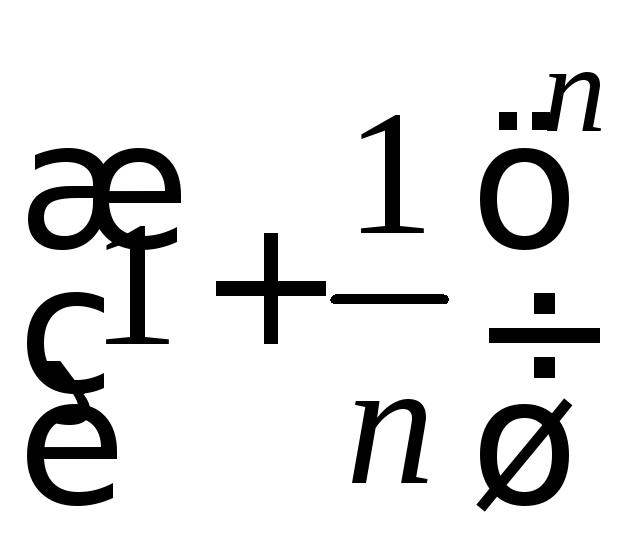, монотонно возрастая, стремится кпри, то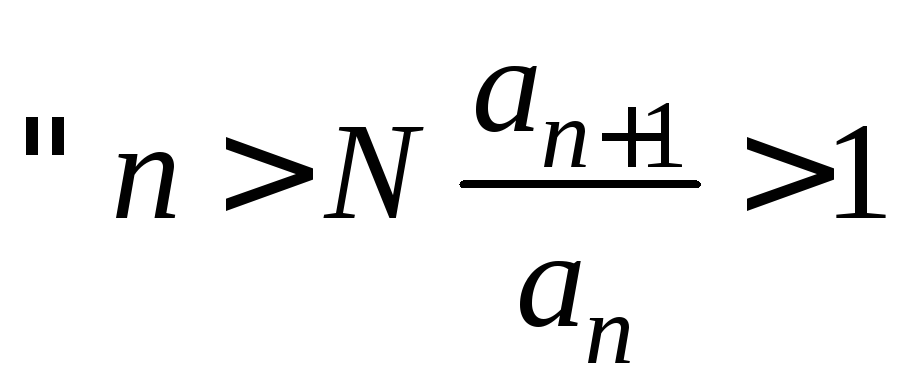. Следовательно,. Поэтомуне стремится к нулю при, необходимый признак сходимости ряда не выполнен, рядрасходится.

Заметим, что 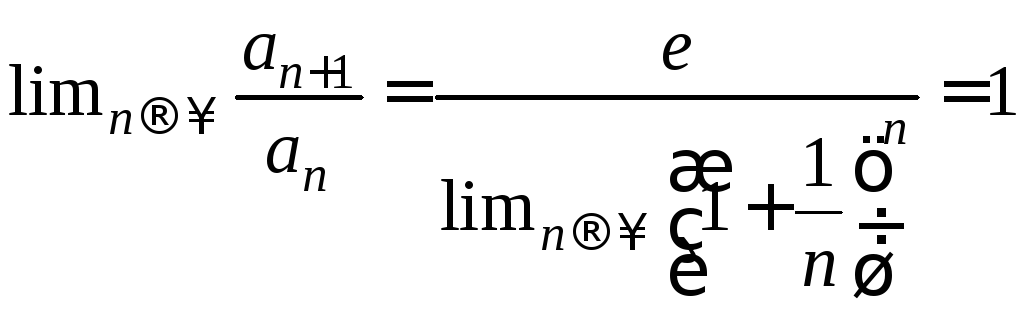. Поэтому признак Даламбера в предельной форме не дает ответ о сходимости или расходимости ряда, хотя признак в конечной форме позволяет установить расходимость ряда.

Радикальный признак Коши

Конечная форма радикального признака Коши.

Пусть , тогда рядсходится.

Пусть , тогда рядрасходится.

Доказательство. Пусть . Тогда, рядсходится по первому признаку сравнения с бесконечно убывающей геометрической прогрессией.

Пусть . Тогда, рядрасходится, так как необходимый признак сходимости ряда не выполнен.

Предельная форма радикального признака Коши.

Пусть , тогда рядсходится.

Пусть , тогда рядрасходится.

Доказательство. Пусть , тогда.

при малом . Рядсходится по конечной форме радикального признака Коши.

Пусть , тогда.при малом. Тогда, рядрасходится, так как необходимый признак сходимости ряда не выполнен.

Пример.

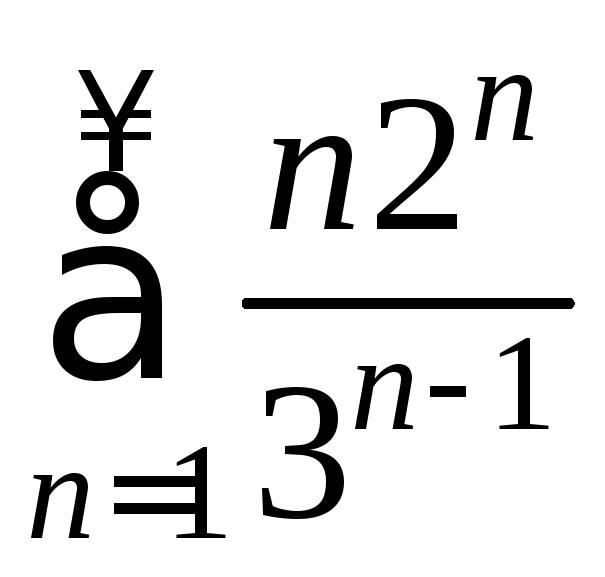
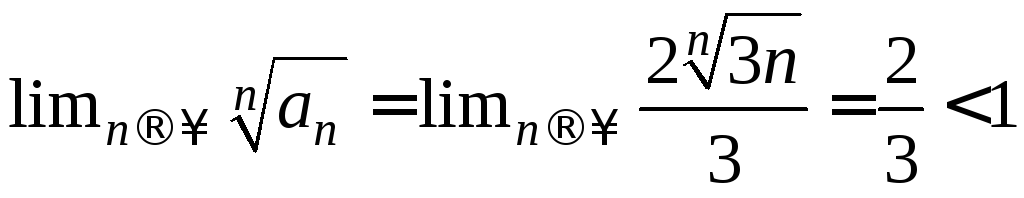, ряд сходится по радикальному признаку Коши в предельной форме.

Замечание. У каждого признака сходимости есть своя «зона нечувствительности». Ни признак Даламбера, ни радикальный признак Коши не позволяют установить расходимость гармонического ряда. Проверьте это. Гармонический ряд расходится, но расходится так слабо, что попадает в «зону нечувствительности» указанных признаков. Интегральный признак Коши имеет меньшую «зону нечувствительности» и позволяет установить расходимость гармонического ряда.

Теорема Дирихле о возможности перестановки местами членов ряда в сходящихся знакоположительных рядах

Пусть - сходящийся знакоположительный ряд. Тогда его члены можно переставлять, менять местами, полученный ряд будет сходиться и иметь ту же сумму.

Доказательство. Проведем доказательство по индукции.

Пусть меняются местами два члена ряда . Тогда в исходном и полученном перестановкой членов ряде частичные суммы, начиная сбудут совпадать. Следовательно, ряд, полученный перестановкой двух членов ряда, будет сходиться и иметь ту же сумму.

Пусть при перестановке местами членов ряда ряд сходится и имеет ту же сумму.

Пусть переставляются членов ряда. Эта перестановка сводится к перестановкечленов ряда, а затем к перестановке еще какого-либо члена с каким-либо другим (перестановке двух членов ряда).

По индуктивному предположению при перестановке местами членов ряда ряд сходится и имеет ту же сумму. Ряд, полученный перестановкой двух членов ряда, будет сходиться и иметь ту же сумму. Следовательно, и при перестановкечленов ряда ряд будет сходиться и иметь ту же сумму.