Добавил:

nyan Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

Математический анализ

Файл:

Задача Коши для волнового уравнения. Формула Даламбера

.pdf

Скачиваний:

Добавлен:

23.01.2017

Размер:

347.01 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

УМФ – семинар – К 5 – 3

Задача Коши для волнового уравнения. Формула Даламбера

№ 370, 438, I, II, 385, 439, 445, 371, III, IV, 372, 446.

1. № 370

Найти общее решение уравнения	(1.1)
utt − a2uxx = 0.

Шаг 1. Находим замену переменных Способ 1 (через уравнения характеристик) Дискриминант характеристической квадра-

тичной формы в данном случае равен a2:

= a122 − a11a22 = a2 > 0,				гиперболический тип.
					√
				dx	a12±	:
Так как a11 = 1 6= 0, составим уравнения характеристик dt =					a11	:
dx
		= ±a,		x = ±at,
	dt	= ±a,		x = ±at,
и первые интегралы имеют вид:
	x + at = c,		x − at = c.
Поэтому заменой, приводящей уравнние (1.1) к каноническому виду, является замена:
		ξ = x + at;
		η = x − at.				(1.2)

Способ 2 (через характеристическую квадратичную форму) В данном случае нам удобнее (и это верно всегда для уравнения гиперболического типа на прямой, если мы хотим явно найти решение) привести квадратичную форму не к обычному её нормальному виду, а к виду

˜ 1 2. Произведём необходимые преобразования:

Q = µ µ

h i

Q(λ1, λ2) = λ21 − a2λ22 = как разность квадратов = (λ1 + aλ2)(λ1 − aλ2) = µ1µ2,

где µ1,2 связаны с λ1,2 по правилу

µ2	=	1	−a λ2
µ1		1	a λ1

Построим матрицу замены переменных:

−a

−1

−

− 21a

= AT

−1

Откуда, учитывая, что λ1 у нас соответствует производной по t, а λ2 – по x, получаем, что замену переменных надо произвести по правилу:

η =

то есть

η = 1

(x at).

ξ =

(x + at);

c Д.С. Ткаченко

−

-1-

−

∂v

∂ξ

ных ∂v∂ξ

УМФ – семинар – К 5 – 3

Итак, оба способа приводят нас к необходимости одной и той же замены (1.2) (с точностью до числового множителя).

Шаг 2. Приведение к каноническому виду

Пусть v(ξ, η) = u(x, t). Замена (1.2) даёт нам следующие соотношения для производных:

ux = vξ + vη,	ut = a (vξ − vη) ,
uxx = vξξ + 2vξη + vηη,	utt = a2 (vξξ − 2vξη + vηη) .
Подставив их в уравнение (1.1), получаем:
utt − a2uxx = a2 (vξξ − 2vξη + vηη) − a2 (vξξ + 2vξη + vηη) = 0,
или, после сокращения,		(1.3)
	vξη = 0.	(1.3)

Шаг 3. Решение уравнения

Уравнение (1.3) решить легко. В самом деле, раз производная по η от функции двух переменравна нулю, то не зависит от η, то есть:

∂v∂ξ = h(ξ).

Проинтегрируем последнее равенство по ξ и учтём, что вместо константы интегрирования надо поставить произвольную функцию от η, так как дифференцирование по ξ любую f2(η) обратит в нуль.

v(ξ, η) = h(ξ)dξ + f2(η) = f1(ξ) + f2(η).

|{z }

=f1(ξ)

Переходя к исходным переменным, получаем:

u(x, t) = f1(x + at) + f2(x − at), (1.4)

где f1,2 – произвольные дважды дифференцируемые функции.

Геометрический смысл равенства (1.4).

Пусть f2 ≡ 0. Тогда в момент времени t = 0 профиль струны задаётся равенством u(x, 0) = f1(x),

в момент времени t = 1 – равенством

u(x, 1) = f1(x + a),

то есть график f1 к моменту t = 1 сдвинулся влево на величину a, и так далее.

Если же, наоборот, f1 ≡ 0. Тогда в момент времени t = 0 профиль струны задаётся равенством u(x, 0) = f2(x),

в момент времени t = 1 – равенством

u(x, 1) = f2(x − a),

то есть график f2 к моменту t = 1 сдвинулся вправо на величину a, и так далее.

Вывод: Решение уравнения колебаний (1.1) представляет собой сумму двух волн, бегущих влево и вправо со скоростью a:

u(x, t) = f1(x + at) + f2(x − at).

| {z } | {z }

←− −→

c Д.С. Ткаченко

-2-

УМФ – семинар – К 5 – 3

2. Формула Даламбера

Рассмотрим задачу Коши на прямой для простейшего случая волнового уравнения:
u(x, 0) = ϕ(x),	x		(	, + );	(2.1)
utt − a2uxx = f(x, t),	x		(−∞, +∞), t (0, +∞);
ut(x, 0) = ψ(x),	x		(−∞, +∞).
		−∞		∞

Теорема 2.1.

Усл. Функции f(x, t) C ((−∞, +∞) × [0, +∞)), ϕ(x), ψ(x) C(−∞, +∞).

Утв. Решение задачи Коши (2.1) задаётся формулой Даламбера:

at + ϕ(x

at)

x+at

t x+a(t−τ)

u(x, t) =

(

+ )

−

ψ(s)ds +

Z Z

f(s, τ)dsdτ. (2.2)

x−at

0 x−a(t−τ)

Доказательство. Полное доказательство мы приведём позже, в теме ¾Применение преобразования Фурье к решению уравнений математической физики¿, № 815, 816. Кроме того, его можно получить элементарной подстановкой формулы Даламбера в равенства (2.1)1. А здесь ограничимся случаем

f(x, t) ≡ 0.

Итак: мы убедились, что всякое решение уравнения utt − a2uxx = 0 представляется в виде

u(x, t) = f1(x + at) + f2(x − at).

(1.4)

Подставим в это равенство начальное условие:

ut(x, 0) = a (f10(x) − f20(x)) = ψ(x).	=
u(x, 0) = f1(x) + f2(x) = ϕ(x);

f1	(y) f2	(y) = 1	y	ψ(s)ds + 2c.
f1	(y) + f2	(y) = ϕ(y);
	−	a	0
			R

Найдя полусумму и полуразность этих равенств, получим:

f1(y) =

ϕ(y)

f1(x + at) =

ϕ(x+at)

+ a 0y

ψ(s)ds + c;

ϕ(y)

откуда

ϕ(x

at)

f2(y) =

− a

ψ(s)ds

−

at) =

−

f2(x

−

x+at

ψ(s)ds + c;

0 x−at

ψ(s)ds − c.

1Заметим, что такой способ позволит убедиться лишь в том, что существует решение (2.1), задаваемое формулой (2.2). Но он не гарантирует, что нет других решений, задаваемых какими-то другими формулами.

c Д.С. Ткаченко

-3-

УМФ – семинар – К 5 – 3

Наконец, подставим f1,2 в формулу (1.4):

−

x+at

− 2a

x−at

−

u(x, t) = f

(x+at)+f

at) =

ϕ(x + at)

ψ(s)ds+c+

ϕ(x − at)

ψ(s)ds

c =

at + ϕ(x

at)

x+at

x−at

(

+ )

−

ψ(s)ds −

ψ(s)ds

+ c − c =

}

x+at

ψ(s)ds

x−at

(

)

−

+ 2a

x+at

at)

ψ(s)ds.

+ ϕ(x

x−at

3. № 438M

Найти решение задачи Коши

utt − a2uxx = βx2, u(x, 0) = e−x,

ut(x, 0) = γ,

x (−∞, +∞), t (0, +∞);	(3.1)
x (−∞, +∞);	(3.1)
x (−∞, +∞).

Чтобы найти решение, нам достаточно применить формулу Даламбера. Вычислим сначала самый сложный входящий в неё интеграл:

21a Z0

t x+a(t−τ)

f(s, τ)dsdτ = 2a Z0

s2dsdτ =

x−a(t−τ)

x+a(t−τ)

τ) dτ =

(x + a(t

− τ))3 − (x

− a(t − τ))3

dτ =

a(t

−

x3 + 3x2(t

dτ =

− τ) + 3x(t − τ)2 + (t − τ)3 − x3 − 3x2(t − τ) + 3x(t − τ)2 − (t − τ)3

= 6a Z

6x2(t − τ) + 2(t − τ)3 dτ = τ − t = p, dτ = dp =

p= t!

6x2(−p) + 2p3 dp = 6a −6x2

p= t + 2

12a 6x2t2

+ t4 .

= 6a Z

p=0

−t

−

c Д.С. Ткаченко

-4-

УМФ – семинар – К 5 – 3

Тогда, из формулы Даламбера получаем:

ϕ x at + ϕ(x

at)

x+at

t x+a(t−τ)

u(x, t) =

( + )

−

ψ(s)ds +

f(s, τ)dsdτ =

x−at

x+at

0 x−a(t−τ)

− −

−

21a

6x2t2 + t4 =

Z γds + 12a

at + e

x+at

= e−x ·

−

x−at

2a (x + at) − (x − at) + 12a 6x2t2 + t4

at + e+at

2 2

= e−

ch at + γt +

6x t + t

12a

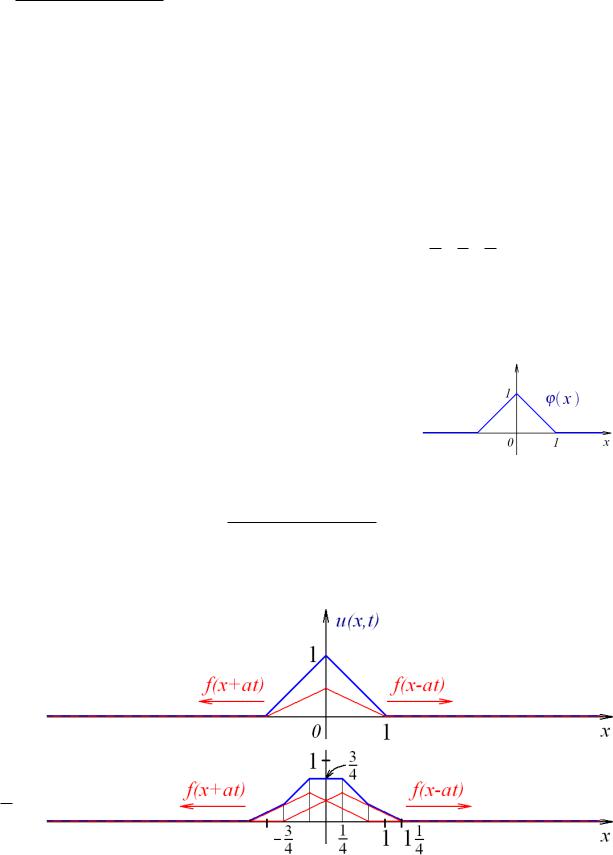
4. № I

Нарисовать профиль бесконечной струны в моменты времени t =

колебания описываются задачей Коши:
u(x, 0) = ϕ(x),	x (			, + );
utt − a2uxx = 0,	x		(−∞, +∞), t (0,
ut(x, 0) = ψ(x),	x		(−∞, +∞),
		−∞		∞

41a , 21a , 43a , a1 , a2 , если её

+∞);

(4.1)

где функция

ψ(x) ≡ 0,

а функция ϕ(x) имеет вид, приведённый на рисунке.

Решение: По формуле Даламбера (2.2) при f ≡ 0 и ψ(x) ≡ 0 получаем:

u(x, t) = ϕ(x + at) + ϕ(x − at) 2

Отсюда можно сделать вывод, что функция u(x, t) есть сумма двух волн одинакового профиля f = ϕ2 , одна из которых бежит влево, а другая вправо. Тогда

при t = 0:

при t = 41a :

c Д.С. Ткаченко

-5-

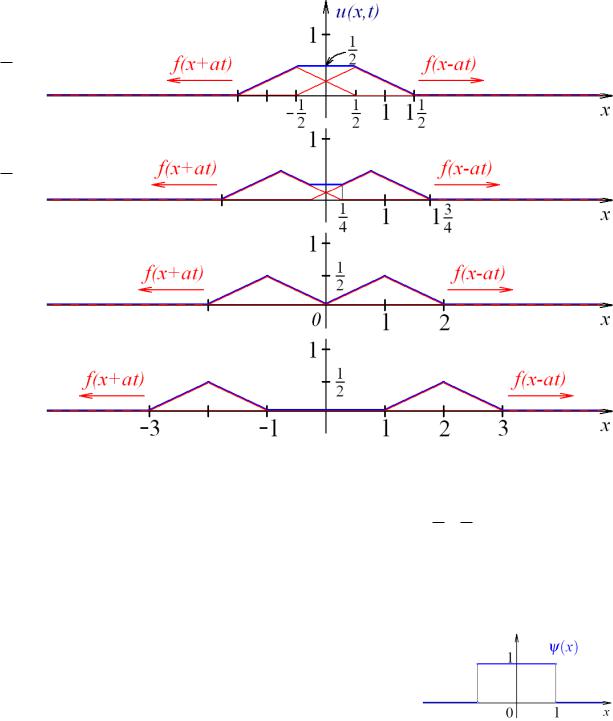
УМФ – семинар – К 5 – 3

при t =

при t = a1 :

при t = a2 :

5. № II

Нарисовать профиль бесконечной струны в моменты времени t =

колебания описываются задачей Коши:
u(x, 0) = ϕ(x),	x (			, + );
utt − a2uxx = 0,	x		(−∞, +∞), t (0,
ut(x, 0) = ψ(x),	x		(−∞, +∞),
		−∞		∞

где функция

ϕ(x) ≡ 0,

а функция ψ(x) имеет вид, приведённый на рисунке.

41a , 21a , a1 , a2 , a3 , если её

+∞);

(5.1)

Решение: По формуле Даламбера (2.2) при f ≡ 0 и ϕ(x) ≡ 0 получаем:

		x+at
u(x, t) =	1	Z	ψ(s)ds = Ψ(x + at) − Ψ(x − at),
u(x, t) =	2a	Z	ψ(s)ds = Ψ(x + at) − Ψ(x − at),
		x−at
где Ψ(y) – некоторая первообразная функции						ψ(x)		, например, функция
где Ψ(y) – некоторая первообразная функции								, например, функция
						2a
						y
		Ψ(y) =		1	Z		ψ(s)ds.
		Ψ(y) =		2a	Z		ψ(s)ds.
						−1

(В качестве нижнего предела мы взяли (−1), поскольку все изменения с функцией ψ(x) происходят только справа от этого числа.)

c Д.С. Ткаченко

-6-

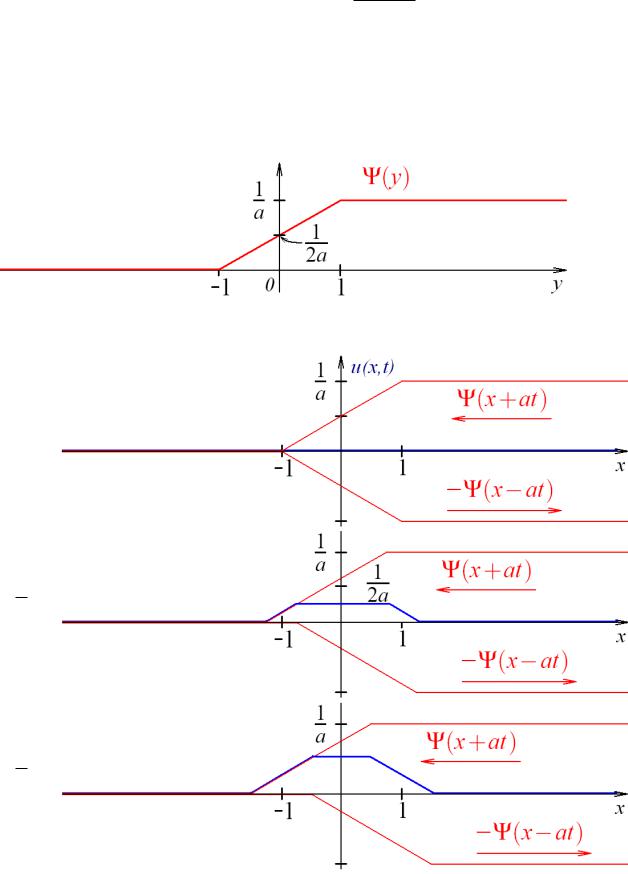
УМФ – семинар – К 5 – 3

Отсюда можно сделать вывод, что функция u(x, t) есть разность двух волн одинакового профиля Ψ, одна из которых бежит влево, а другая вправо. Причём из волны, бегущей влево, вычитается волна, бегущая вправо. Найдём Ψ(y) для нашего случая:

Ψ(y) = 2a

ψ(s)ds =

2a ,

когда

[−1, 1];

когда

( ,

1];

y+1

−∞ −

1 ,

когда

y [1, +

−

∞

График этой функции выглядит так:

Поэтому профиль струны будет принимать в различные моменты времени форму:

при t = 0:

при t = 41a :

при t = 21a :

c Д.С. Ткаченко

-7-

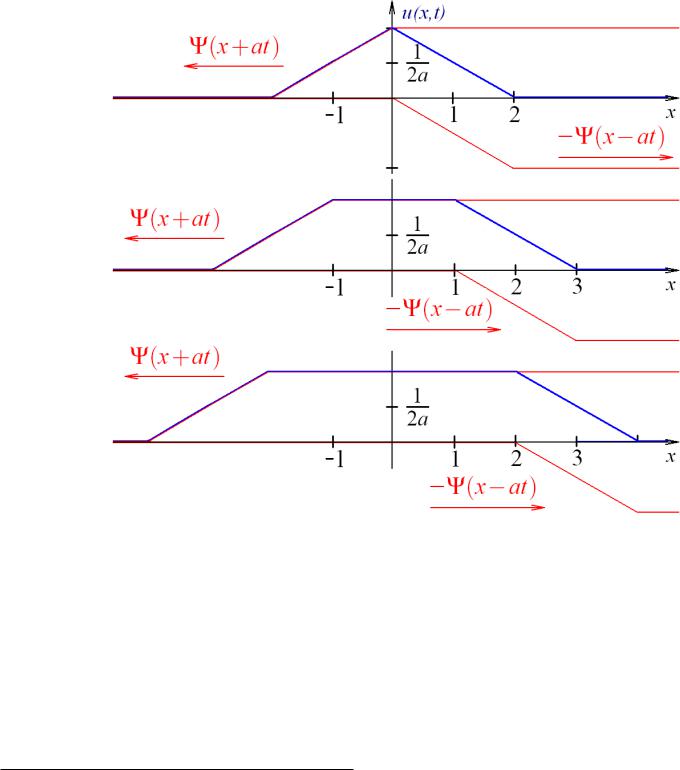
УМФ – семинар – К 5 – 3

при t = a1 :

при t = a2 :

при t = a3 :

6. № 385

Найти решение задачи:				(
u(0,−y) = ϕ(y),			y		, + );	(6.1)
uxx		2uxy + 4ey = 0,	x (0, +∞), y (−∞, +∞);
ux(0, y) = ψ(y),			y	(−∞, +∞).
Прежде чем решать				−∞	∞
	эту задачу, заметим, что если переименовать переменную x в t, а y – в x,

то получится обычная задача Коши для УЧП 2-го порядка.

Шаг 1. Находим замену переменных Способ 1 (через уравнения характеристик) Дискриминант характеристической квадратичной формы в данном случае равен a2:

= a122 − a11a22 = (−1)2 − 1 · 0 = 1 > 0,					гиперболический тип.
				dy	√
				dy	√
Так как a11 = 1 6= 0, составим уравнения характеристик dx =					a12±	:
Так как a11 = 1 6= 0, составим уравнения характеристик dx =					a11	:
	dx = −1 ± 1 =	−2,		y = −2x + c,
	dy	0,		y = c,
и первые интегралы имеют вид:
	y = c,		y + 2x = c.

c Д.С. Ткаченко

-8-

УМФ – семинар – К 5 – 3

Поэтому заменой, приводящей уравнние (6.1) к каноническому виду, является замена:

ξ = y;

(6.2)

η = y + 2x.

Способ 2 (через характеристическую квадратичную форму) В данном случае нам удоб-

нее (как всегда для уравнения гиперболического типа на прямой) привести квадратичную

форму не к обычному её нормальному виду, а к виду ˜ 1 2. Произведём необходимые

Q = µ µ

преобразования:

Q(λ1, λ2) = λ21 − 2λ1λ2 = (λ1 − 2λ2)λ1 = µ1µ2,

где µ1,2 связаны с λ1,2 по правилу

µ2	1		0	λ2
µ1	=	1	−2	λ1

Построим матрицу замены переменных:

= AT −1 =	1	0	−1	=	0	− 21
	2	2			1	1
			1
						2

Откуда, учитывая, что λ1 у нас соответствует производной по x, а λ2 – по y, получаем, что замену переменных надо произвести по правилу:

η	=		−		y	то есть		−		·
		0	1	1			ξ =		1		y;
		1	1	2			η = 1 (2x + y).
ξ				2	x				2
			2					2

Итак, оба способа приводят нас к необходимости одной и той же замены (6.2) (с точностью до числового множителя).

Шаг 2. Приведение к каноническому виду

Пусть v(ξ, η) = u(x, t). Замена (6.2) даёт нам следующие соотношения для производных:

ux = 2vη,	uy = vξ + vη,
uxx = 4vηη,	uxy = 2 (vξη + vηη) .
Подставив их в уравнение (6.1), получаем:
uxx − 2uxy + 4ey = 4vηη − 2 · 2 (vξη + vηη) + 4eξ = 0,
или, после сокращения,		(6.3)
vξη = eξ.		(6.3)

Шаг 3. Решение уравнения

Уравнение (6.3) решить легко – достаточно проинтегрировать его по ξ и η. Сначала интегри-

руем по η:

vξ = η · eξ + h(ξ).

(Напомним, что функция h(ξ) появилась вместо и в качестве константы интегрирования.) Теперь проинтегрируем последнее равенство по ξ и учтём, что вместо константы интегрирования надо поставить произвольную функцию от η:

v(ξ, η) = η · eξ + h(ξ)dξ + f2(η) = η · eξ + f1(ξ) + f2(η).

|{z }

=f1(ξ)

c Д.С. Ткаченко

-9-

УМФ – семинар – К 5 – 3

Переходя к исходным переменным, получаем:

u(x, t) = (y + 2x) · ey + f1(y) + f2(y + 2x),

(6.4)

где f1,2 – произвольные дважды дифференцируемые функции.

Шаг 4. Использование начальных условий

Подставляя общее решение (6.4) уравнения в начальные условия, получаем:

u(0, y) = ϕ(y), ux(0, y) = ψ(y),

yey + f1(y) + f2(y) = ϕ(y),

2ey + 2f20(y) = ψ(y).

Из последнего уравнения сразу находится f2(s):

	s		s	s
f2(s) = Z	2ψ(y) − ey dy + c =	2Z		s	= 2Ψ(s) − es + 1 + c1 =
f2(s) = Z	2ψ(y) − ey dy + c =	2Z		ψ(y)dy − ey 0 + c1	= 2Ψ(s) − es + 1 + c1 =
0	1	1			1
0		0

| {z }

Ψ(s)

= hc = c1 + 1i = 12Ψ(s) − es + c.

Подставляя найденную функцию f2(s) = 12 Ψ(s) − es + c, в первое начальное условие, найдём

f1(s):

f1(s) = ϕ(s) − 12Ψ(s) + es − c − ses = ϕ(s) − 12Ψ(s) + (1 − s)es − c.

Осталось подставить

f1(s) = ϕ(s) −	1	Ψ(s) + (1	− s)es − c	и f2(s) =	1	Ψ(s) − es + c

	2				2

вформулу общего решения (6.4).

u(x, t) = (y + 2x) · ey + f1(y) + f2(y + 2x) =

=(y + 2x) · ey + ϕ(y) − 12Ψ(y) + (1 − y)ey − c + 12Ψ(y + 2x) − ey+2x + c =

	y+2x		y	ψ(y)dy =
= (2x + 1) · ey − ey+2x + ϕ(y) + 2 Z		ψ(y)dy − Z		ψ(y)dy =
1
	0		0

= (2x + 1) · ey − ey+2x + ϕ(y) +

Ответ:

y+2x

1 Z

ψ(y)dy.

u(x, t) = (2x + 1) · ey − ey+2x + ϕ(y) + 2	Zy	ψ(y)dy.
1

c Д.С. Ткаченко

-10-

1 / 21 2 > Следующая >>>

Соседние файлы в папке Учебники и методички

#
23.01.201738.05 Кб8pic364.png
#
23.01.201719.28 Кб8pic560.png
#
23.01.2017347.01 Кб46Задача Коши для волнового уравнения. Формула Даламбера.pdf
#
23.01.20172.03 Mб46Кратные, криволинейные и поверхностные интегралы.doc
#
23.01.2017435.55 Кб58Криволинейные интегралы - МГТУ им. Н. Э. Баумана.pdf
#
23.01.2017176.93 Кб14Криволинейный и поверхностный интегралы первого рода.pdf
#
23.01.20174.18 Mб169Математический анализ. Курс лекций.doc
#
23.01.2017668.78 Кб57Поверхностные интегралы первого рода.pptx