
- •Математический анализ
- •Часть 2. Числовые и функциональные ряды 49
- •Часть1. Кратные и криволинейные интегралы, теория поля Лекция 1. Двойной интеграл Задача об объеме цилиндрического тела.
- •Двойной интеграл
- •Вычисление двойного интеграла в декартовой системе координат
- •Геометрический и физический «смысл» двойного интеграла
- •Лекция 2. Приложения двойного интеграла
- •Приложения двойного интеграла
- •Вычисление площади поверхности с помощью двойного интеграла
- •Вычисление статических моментов, координат центра тяжести, моментов инерции
- •Замечание о несобственных двойных интегралах
- •Лекция 3 Тройной интеграл Задача о массе пространственного тела
- •Свойства тройного интеграла
- •Вычисление тройного интеграла в декартовой системе координат
- •Лекция 4. Приложения тройного интеграла
- •Лекция 5 Криволинейные интегралы 1 и 2 рода, их свойства Задача о массе кривой. Криволинейный интеграл 1 рода
- •Свойства криволинейного интеграла первого рода
- •Вычисление криволинейного интеграла первого рода
- •Криволинейный интеграл 2 рода Задача о работе силы
- •Теорема существования.
- •Свойства криволинейного интеграла 2 рода
- •Вычисление криволинейного интеграла второго рода
- •Лекция 6. Формула Грина
- •Вычисление площади области по формуле Грина
- •Полный дифференциал и его вычисление
- •Формула Ньютона – Лейбница
- •Теорема (о полном дифференциале) для пространственной кривой
- •Вычисление криволинейного интеграла от полного дифференциала
- •Формула Грина для многосвязной области
- •Лекция 7. Поверхностные интегралы Задача о массе поверхности
- •Свойства поверхностного интеграла первого рода
- •Вычисление поверхностного интеграла первого рода
- •Поверхностный интеграл второго рода
- •Задача о потоке жидкости через поверхность
- •Запись поверхностного интеграла второго рода
- •Лекция 8. Скалярное и векторное поля
- •Скалярные поля.
- •Векторное поле
- •Формула Остроградского – Гаусса
- •Инвариантное определение дивергенции
- •Свойства дивергенции
- •Соленоидальное поле и его свойства
- •Свойства соленоидального поля
- •Лекция 9 Формула Стокса Ротор векторного поля
- •Свойства ротора
- •Теорема Стокса
- •Инвариантное определение ротора
- •Потенциальное поле и его свойства
- •Свойства потенциального поля.
- •Оператор Гамильтона
- •Дифференциальные операции второго порядка
- •Гармоническое поле
- •Часть 2. Числовые и функциональные ряды Лекция 10. Числовые ряды и их свойства
- •Необходимый признак сходимости ряда.Если ряд сходится, то .
- •Критерий Коши сходимости ряда
- •Свойства сходящихся рядов
- •Лекция 11 Знакоположительные ряды
- •Интегральный признак Коши
- •Признаки сравнения рядов
- •Признак Даламбера
- •Радикальный признак Коши
- •Теорема Дирихле о возможности перестановки местами членов ряда в сходящихся знакоположительных рядах
- •Лекция 12. Знакопеременные ряды
- •Теорема о перестановке членов в абсолютно сходящихся рядах.
- •Теорема Римана.
- •Знакочередующиеся ряды
- •Признак Лейбница.
- •Функциональные ряды Лекция 13. Равномерно сходящиеся ряды
- •Признак Вейерштрасса равномерной сходимости ряда.
- •Свойства равномерно сходящихся функциональных рядов.
- •Лекция 14. Степенные ряды
- •Теорема Абеля.
- •Радиус сходимости и интервал сходимости степенного ряда
- •Определение радиуса и интервала сходимости степенного ряда
- •Лекция 15. Ряд Тейлора Ряд Тейлора
- •Разложение в ряд Маклорена основных элементарных функций
- •Применение степенных рядов
- •Ряды Фурье. Лекция 16. Задача о наилучшем приближении
- •Задача о наилучшем приближении в н (гильбертовом пространстве)
- •Лекция 17. Ряд Фурье по тригонометрической системе функций (тригонометрический ряд Фурье)
- •Связь между гладкостью функции и порядком малости коэффициентов Фурье
- •Разложения в ряд Фурье функций, заданных на отрезке
Лекция 8. Скалярное и векторное поля
Говорят, что в области (плоской или пространственной) задано скалярное поле (M), если в этой области задана скалярная функция (M).
Говорят,
что в области (плоской или пространственной)
задано векторное
поле
![]() (M),
если в этой области задана векторная
функция
(M),
если в этой области задана векторная
функция
![]() (M).
(M).
Например, масса или температура частиц в комнате – скалярные поля, скорость или силы взаимодействия частиц – векторные поля.
В интегралах первого рода :двойных, криволинейных, поверхностных мы имели дело со скалярным полем – распределением масс точек кривой или поверхности в пространстве.
В интегралах второго рода вычислялись характеристики векторных полей: работа векторного поля (силового поля) в криволинейном интеграле, поток векторного поля в поверхностном интеграле.
Рассмотрим подробнее основные характеристики скалярных и векторных полей.
Скалярные поля.
Линии уровня плоского поля (x, y) – кривые, на которых значения функции постоянны (x, y) = С.
Например, линии равной высоты, нанесенные на географической карты (h (x, y) = 0 – уровень моря, h = 7000м – немногие горные вершины, h = - 10000м – самые глубокие океанские впадины).
Поверхности уровня пространственного поля (x, y, z) – поверхности, на которых значения функции постоянны (x, y, z) = С.
Например, поверхности равной температуры или давления в атмосфере. Любая линия на поверхности уровня – это линия уровня.
Пример.
Задано поле
![]() .
При С > 0 поверхности уровня –
однополостные гиперболоиды, при С = 0
поверхность уровня – конус, при С < 0
поверхности уровня – двуполостные
гиперболоиды.
.
При С > 0 поверхности уровня –
однополостные гиперболоиды, при С = 0
поверхность уровня – конус, при С < 0
поверхности уровня – двуполостные
гиперболоиды.
Линии или поверхности различных уровней не пересекаются.
Чем чаще (гуще) поверхности или линии уровня, тем интенсивнее изменение поля.
Градиент
поля – вектор
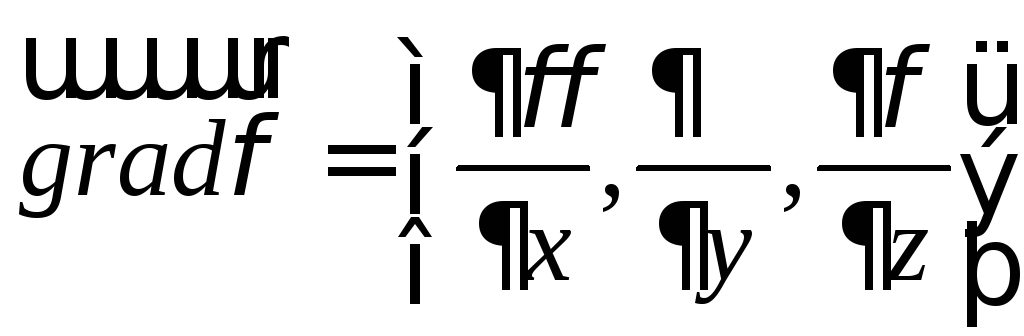 .
.
Утверждение. Градиент скалярного поля ортогонален его поверхности уровня.
Доказательство. Пусть точка (x, y, z) остается на поверхности уровня g(x, y, z) = 0 при вариациях переменных. Тогда равенство превращается в тождество, а тождество можно дифференцировать.
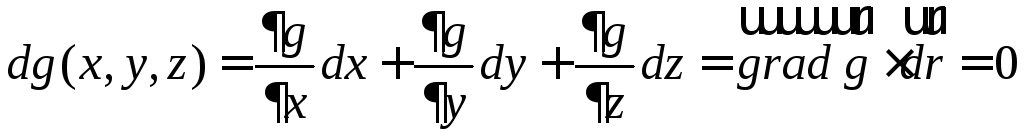 .
.
Вектор
![]() (x,
y,
z)
- это вектор, касательный в точке (x,
y,
z)
к любой кривой, лежащей на поверхности
уровня, проходящей через эту точку.
Поэтому в точке (x,
y,
z)
вектор градиента ортогонален всем
касательным к линии уровня, проходящим
через эту точку. Следовательно, он
ортогонален касательной плоскости к
поверхности уровня и направлен по
нормали к поверхности уровня.
(x,
y,
z)
- это вектор, касательный в точке (x,
y,
z)
к любой кривой, лежащей на поверхности
уровня, проходящей через эту точку.
Поэтому в точке (x,
y,
z)
вектор градиента ортогонален всем
касательным к линии уровня, проходящим
через эту точку. Следовательно, он
ортогонален касательной плоскости к
поверхности уровня и направлен по
нормали к поверхности уровня.
Производная
скалярного поля по направлению
![]() определяется как
определяется как
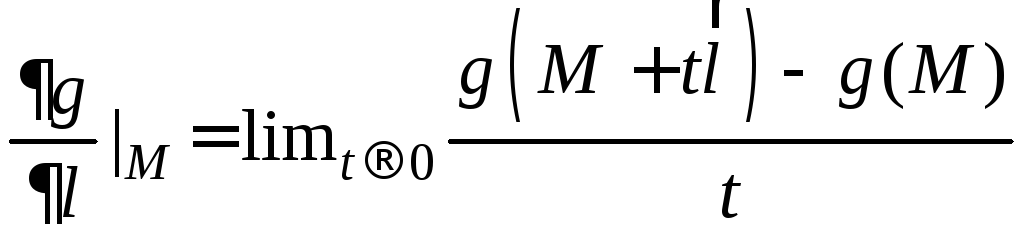 .
Известно из теории функций многих
переменных, чтопроизводная
по направлению есть проекция градиента
на данное направление
.
Известно из теории функций многих
переменных, чтопроизводная
по направлению есть проекция градиента
на данное направление
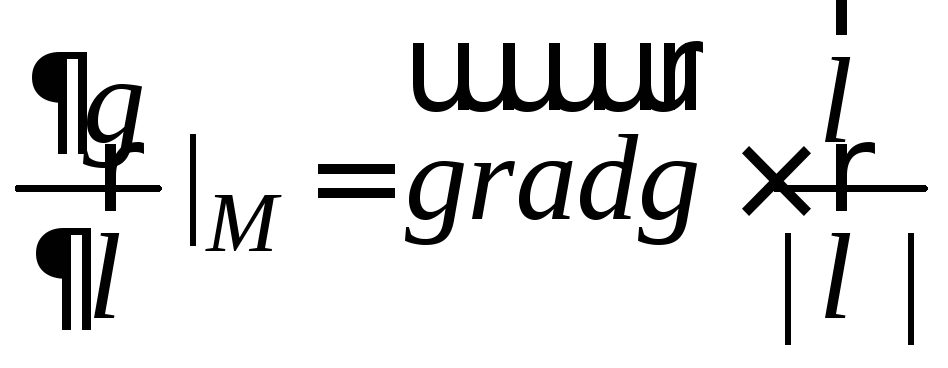 .
.
Пример. Найти производную скалярного поля g(x, y, z) = x2 + y2 + z3 по направлению {1,3,2} в точке (1,0,4)
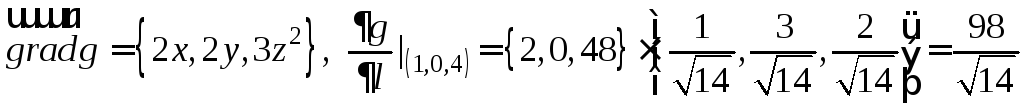 .
.
![]()
Векторное поле
Векторная линия - линия, в каждой точке которой вектор поля направлен по касательной к ней.
Уравнения
векторной линии
легко получить из условия коллинеарности
векторов поля
![]() и касательной
и касательной![]()
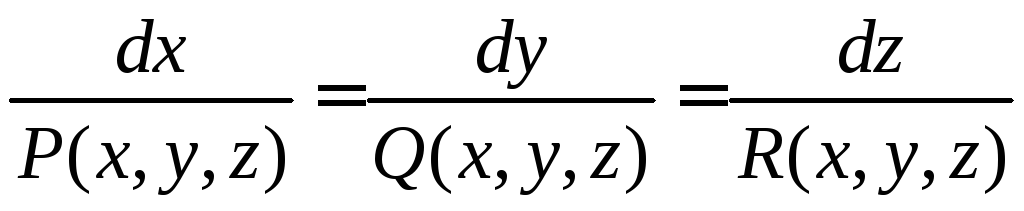 .
.
Пример.
Написать
уравнения векторных линий векторного
поля
![]()
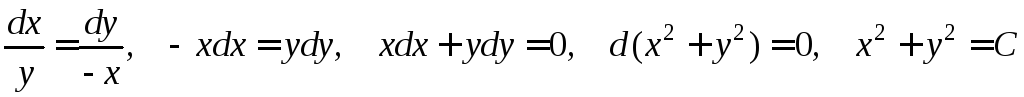 -
линии уровня – окружности (С>0).
-
линии уровня – окружности (С>0).
Векторной трубкой называется поверхность, образованная векторными линиями.
Формула Остроградского – Гаусса
Пусть
компоненты векторного поля
![]() непрерывны и имеют непрерывные частные
производные в пространственно односвязной
замкнутой областиV
и на ее кусочно гладкой границе
непрерывны и имеют непрерывные частные
производные в пространственно односвязной
замкнутой областиV
и на ее кусочно гладкой границе
![]() .
.
Тогда справедлива формула Остроградского – Гаусса
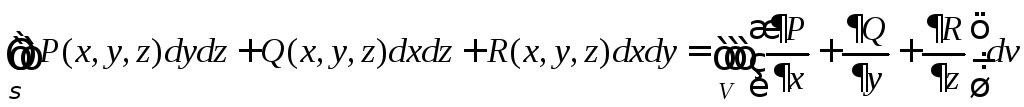 .
.
Заметим,
что левая часть формулы представляет
собой поток векторного поля
![]() через поверхность
через поверхность![]() .
.
Доказательство. 1) Формула Остроградского – Гаусса, в силу произвольности P, Q, R состоит из трех частей, в каждую из которых входит одна из компонент векторного поля P, Q, R. В самом деле, можно взять P = 0, Q = 0 и доказывать отдельно часть формулы в которую входит только R. Остальные части формулы (при P = 0, R = 0, Q = 0, R = 0) доказываются аналогично. Будем доказывать часть формулы
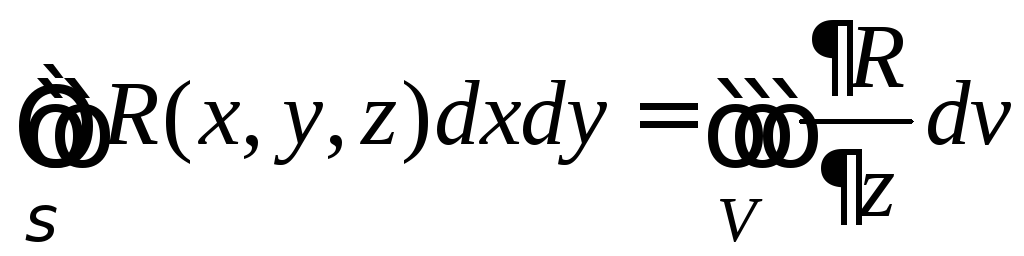
2) Для доказательства выбранной части формулы представим пространственную область V в виде объединения конечного числа цилиндрических тел, не имеющих общих внутренних точек, с образующими, параллельными оси OZ. Доказательство можно проводить для цилиндрического тела. В самом деле, тройной интеграл в правой части равен сумме тройных интегралов по цилиндрическим телам (свойство аддитивности). Поверхностный интеграл в левой части также равен сумме поверхностных интегралов по полным поверхностям цилиндрических тел, причем при суммировании интегралы по общим границам соседних цилиндрических тел будут сокращаться из-за противоположного направления внешних нормалей на общих границах.
Итак,
будем доказывать соотношение
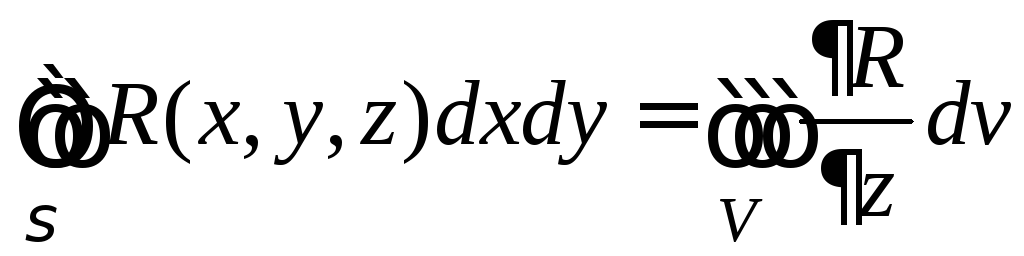 для цилиндрического телаV,
проектирующегося в область D
на плоскости OXY.
Пусть «верхняя» граница цилиндрического
тела – поверхность
для цилиндрического телаV,
проектирующегося в область D
на плоскости OXY.
Пусть «верхняя» граница цилиндрического
тела – поверхность
![]() описывается уравнением
описывается уравнением![]() ,
«нижняя» граница – поверхность
,
«нижняя» граница – поверхность![]() описывается уравнением
описывается уравнением![]() .
Боковую поверхность цилиндрического
тела, параллельную осиOZ,
обозначим
.
Боковую поверхность цилиндрического
тела, параллельную осиOZ,
обозначим
![]() .
.
Сразу
заметим, что поток векторного поля через
боковую поверхность равен нулю.
Действительно,
![]() ,
так как нормаль на боковой поверхности
ортогональна осиOZ
и
,
так как нормаль на боковой поверхности
ортогональна осиOZ
и
![]() .
.
Заметим
также, что на «верхней» поверхности
![]()
![]() ,
а на «нижней поверхности
,
а на «нижней поверхности![]()
![]() .
Поэтому при переходе от поверхностного
интеграла по
.
Поэтому при переходе от поверхностного
интеграла по![]() к двойному интегралу по областиD
и обратно надо менять знак, а при переходе
от поверхностного интеграла по
к двойному интегралу по областиD
и обратно надо менять знак, а при переходе
от поверхностного интеграла по![]() к двойному интегралу по областиD
и обратно менять знак не надо.
к двойному интегралу по областиD
и обратно менять знак не надо.
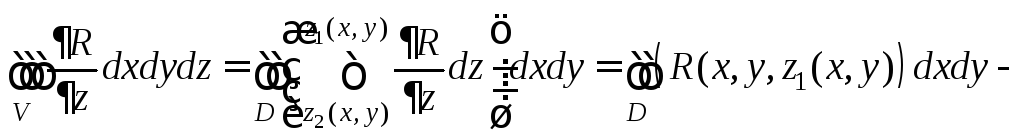
![]()
![]()
|
D |
=
Таким
образом, соотношение
|
Замечание. Формулу Остроградского – Гаусса можно записать в «полевом» виде
![]() - поток векторного
поля через замкнутую поверхность
- поток векторного
поля через замкнутую поверхность
![]() равен объемному интегралу от дивергенции
поля по области, ограниченной поверхностью
равен объемному интегралу от дивергенции
поля по области, ограниченной поверхностью![]() .
.
Дивергенция
векторного поля (расходимость)
есть
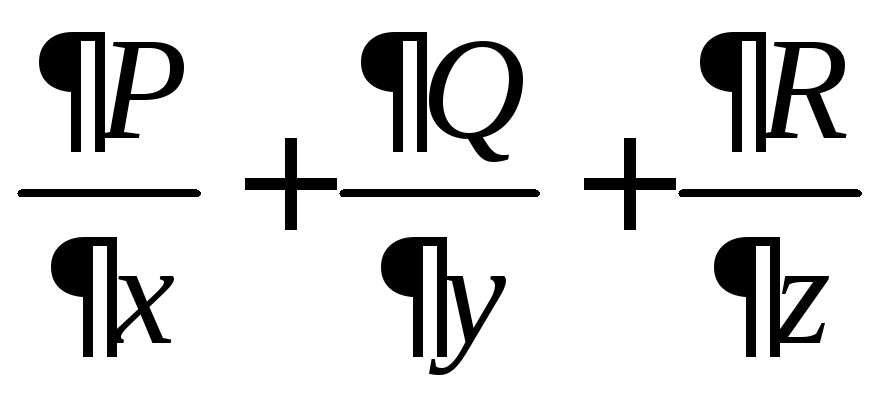 .
.
Дивергенция – это характеристика векторного поля, инвариантная относительно системы координат. Покажем это.






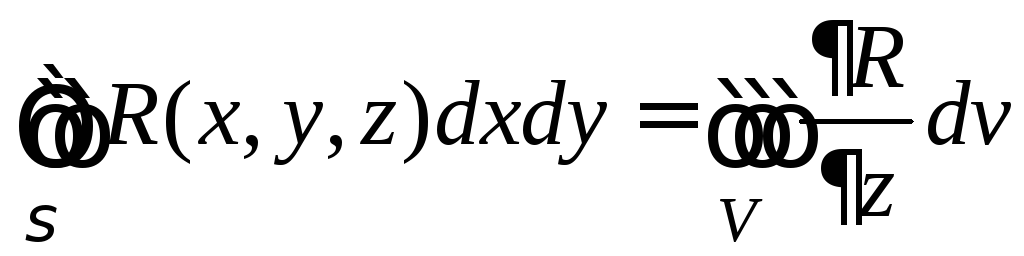 доказано.
доказано.