Литература к лекции 34-35
1. Высшая математика: Учебник для вузов: В 3-х т. Т. 3 : Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного / Я. С. Бугров, С. М. Никольский ; Под ред. В.А. Садовничего. - 7-е стер. изд. - М. : Дрофа, 2005. - 512 с.
Лекция 36. Элементы теории поля. Потенциальное и соленоидальное поля. Оператор Гамильтона.
Основные понятия: скалярное поле, векторное поле, градиент, ротор, дивергенция, потенциальное поле, соленоидальное поле, оператор Гамильтона.
Говорят,
что в области
(двухмерной или трехмерной) задано поле,
если каждой точке этой области
соответствует определенное значение
некоторой величины – числовой или
векторной. Если в каждой точке области
задана скалярная функция
,
Ее называют скалярным полем. Если в
области
задана векторная функция
,
ее называют векторным полем. Иногда
полем называют область ,
то есть область определения скалярной
или векторной функции.
Для
наглядного представления скалярного
поля его для двухмерного случая
характеризуют линиями уровня, а для
трехмерного скалярного поля -
поверхностями уровня. Поверхности
уровня описываются уравнением
.
Поверхности,
овевающие различным значениям поля
,
заполняют
всю область, в которой определено поле.
Векторное поле характеризуется векторными линиями – кривыми, у которых касательные в каждой точке направлены вдоль заданного в этой точке вектора. Для векторного поля
заданного
в декартовой системе своими координатами
уравнение векторных линий имеет вид
.
Наряду с поверхностями уровня и векторными линиями скалярные и векторные поля характеризуются своими дифференциальными свойствами. Поверхности уровня и векторные линии относятся к общей геометрии полей, тогда как дифференциальные свойства полей относятся к их точечным характеристикам. Для формального введения дифференциальных характеристик удобно пользоваться символическим вектором набла
Символический
вектор набла приобретает значение
реального вектора только в комбинации
со скалярными и векторными полями. Для
того чтобы этот оператор воздействовал
на поле, он должен стоять слева от него.
При действии оператора
на скалярное поле
получаем векторное поле
Символический
вектор набла может действовать на
векторное поле
по правилу скалярного произведения. В
этом случае получаем скалярное поле,
которое называется дивергенцией
Если
оператор
действует на векторное поле по правилу
векторного произведения, мы получаем
новое векторное поле, которое называют
ротором
.
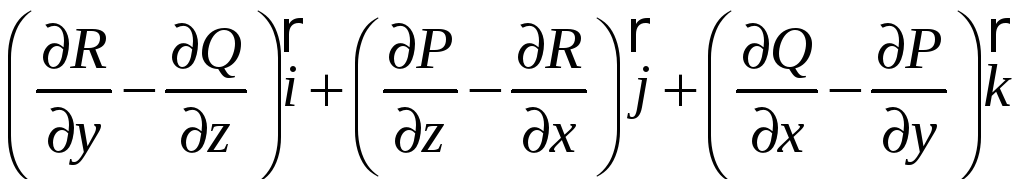Точечная
характеристика скалярного поля
-
это вектор, проекция которого на данное
направление определяет изменение поля
в этом направлении (равна производной
поля по данному направлению). Максимальное
изменение поля
происходит в направлении
.
Физический
и геометрический смысл дифференциальных
характеристик векторного поля
,
а именно
и
,
выяснится после рассмотрения криволинейного
и поверхностного интегралов от векторных
полей (криволинейных и поверхностных
интегралов второго рода).
Литература к лекции 36
1. Высшая математика: Учебник для вузов: В 3-х т. Т. 3 : Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного / Я. С. Бугров, С. М. Никольский ; Под ред. В.А. Садовничего. - 7-е стер. изд. - М. : Дрофа, 2005. - 512 с.