
- •Модуль 7
- •Необходимое условие сходимости ряда
- •Задачи для самостоятельного решения
- •Знакочередующиеся ряды. Признак Лейбница
- •Условная сходимость. Признак Абеля-Дирихле
- •Задачи для самостоятельного решения
- •Занятие 10 Степенные ряды
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Занятия 12 Тригонометрический ряд Фурье функции на интервале
- •Ряд Фурье функции на интервале
- •Задачи для самостоятельного решения
- •Преобразование Фурье
- •Косинус- преобразование и синус-преобразование Фурье
- •Задачи для самостоятельного решения
Задачи для самостоятельного решения
Разложить указанные функции в ряд Фурье по тригонометрической системе, указать период функции и построить ее график.
1.
![]() ;
;
2.
![]() по синусам
по синусам
![]() ;
;
3.
![]() по косинусам,
по косинусам,![]() ;
;
4.
![]() по косинусам;
по косинусам;
5.
![]() по синусам;
по синусам;
6.
![]() ;
;
7.
![]() ;
;
8.
![]() ;
;
9.
![]() ;
;
10.
![]() .
.
Ответы
1.
 .
2.
.
2.
 .3.
.3.
 .4.
.4.  .5.
.5.
 .6.
.6.  .7.
.7.  .8.
.8. 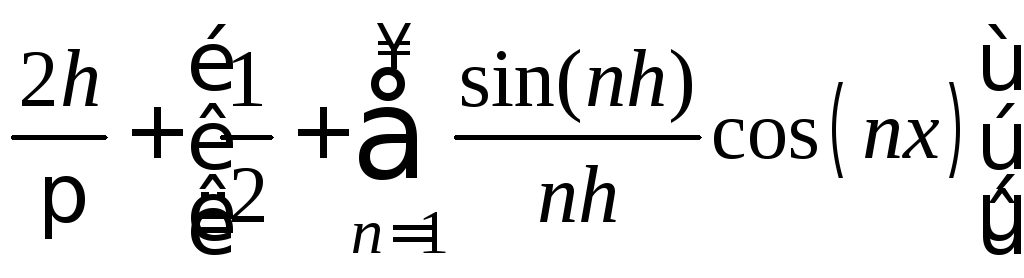 .
9.
.
9.
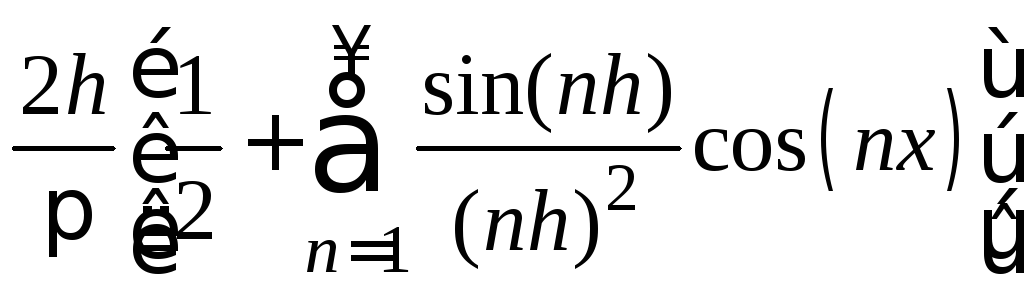 .
10.
.
10. 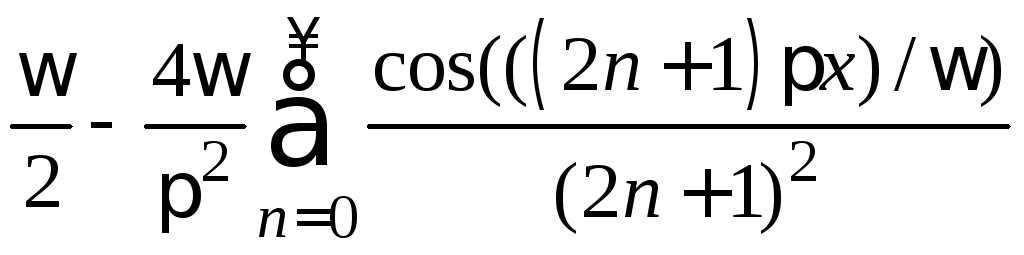 .
.
Преобразование Фурье
Свертка
Фурье двух абсолютно интегрируемых на
всей прямой функций определяется
следующим образом: .
.
Прежде,
чем найти преобразование Фурье функции
![]() ,
вычислим интеграл Эйлера-Пуассона, тем
самым убедимся в абсолютной интегрируемости
этой функции на всей прямой.
,
вычислим интеграл Эйлера-Пуассона, тем
самым убедимся в абсолютной интегрируемости
этой функции на всей прямой.
Пример.
Вычислить интеграл Эйлера-Пуассона: (
(![]() ).
).
Решение.
Вычислим сначала
 ,
а именно, используя искусственный прием,
покажем, что
,
а именно, используя искусственный прием,
покажем, что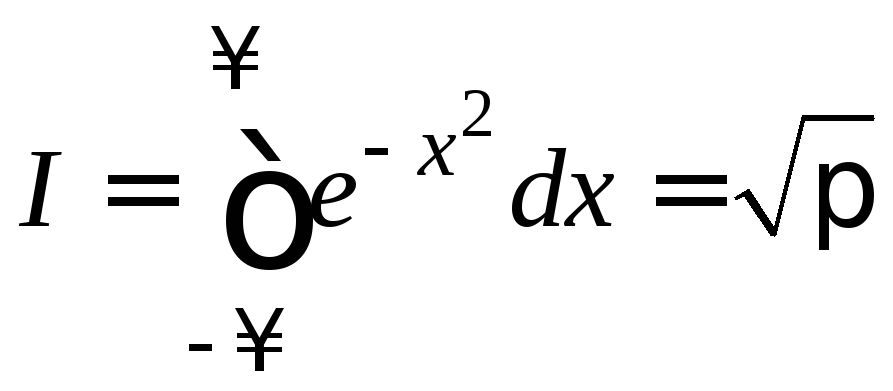 .
Действительно,
.
Действительно,
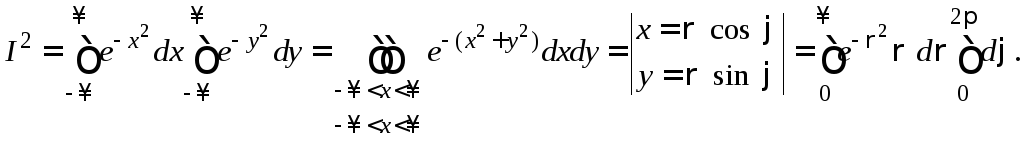
Отсюда

Заменой
переменной получим
 для любого
для любого![]() .
.
Ответ:
 .
.
Пример.
Найти преобразование Фурье функции
![]() (
(![]() ).
).
Решение.
По определению преобразования Фурье
 .
Под интегралом аналитическая функция,
не имеющая особенность в конечной части
плоскости и стремящаяся к нулю вдоль
каждой прямой параллельной действительной
оси. В силу теоремы Коши интеграл не
изменит своего значения, если его взять
не по действительной оси, а вдоль любой
прямой
.
Под интегралом аналитическая функция,
не имеющая особенность в конечной части
плоскости и стремящаяся к нулю вдоль
каждой прямой параллельной действительной
оси. В силу теоремы Коши интеграл не
изменит своего значения, если его взять
не по действительной оси, а вдоль любой
прямой![]() (
(![]() -
константа), параллельной действительной
оси.
-
константа), параллельной действительной
оси.

Отсюда
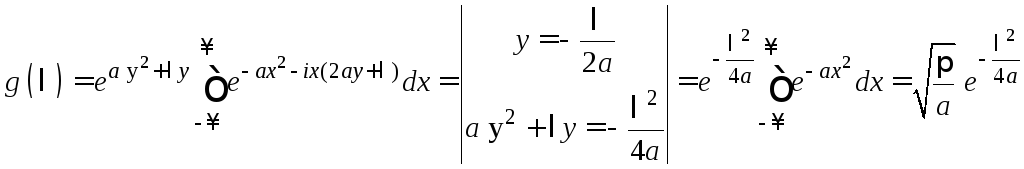 .
.
Ответ:
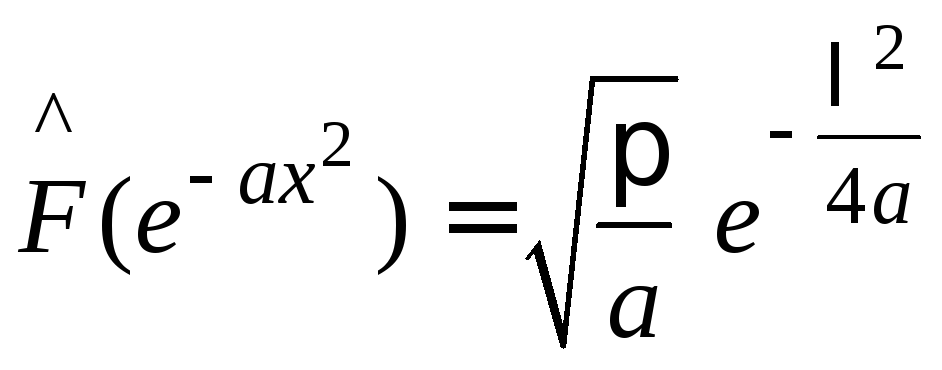 .
.
Пример.
Найти преобразование Фурье по переменной
![]() функции
функции (
(![]() ),
зависящей от положительного параметра
),
зависящей от положительного параметра![]() .
.
Решение.
Из предыдущего примера следует, что
 для любого
для любого![]() .
Отсюда, учитывая линейность преобразования
Фурье, получим
.
Отсюда, учитывая линейность преобразования
Фурье, получим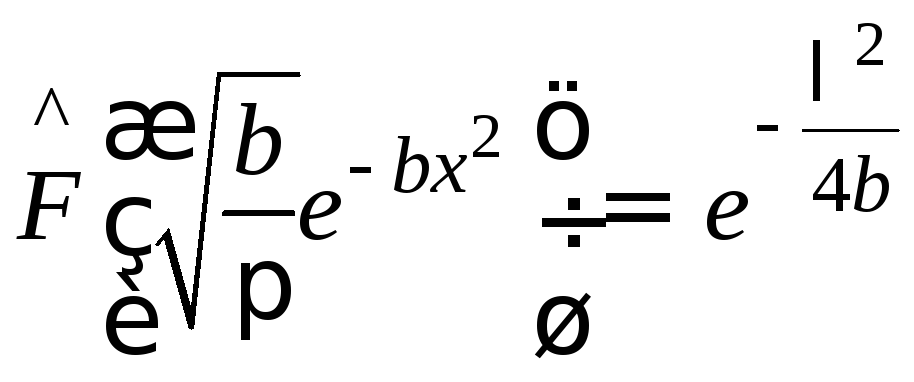 .
Полагая в последнем равенстве
.
Полагая в последнем равенстве ,
получим
,
получим .
.
Ответ:
 .
.
Пример.
Предполагая производную
![]() от абсолютно интегрируемой на всей
прямой функции
от абсолютно интегрируемой на всей
прямой функции![]() ,
также абсолютно интегрируемой на всей
прямой, найти зависимость между их
преобразованиями Фурье.
,
также абсолютно интегрируемой на всей
прямой, найти зависимость между их
преобразованиями Фурье.
Решение.
Имеем
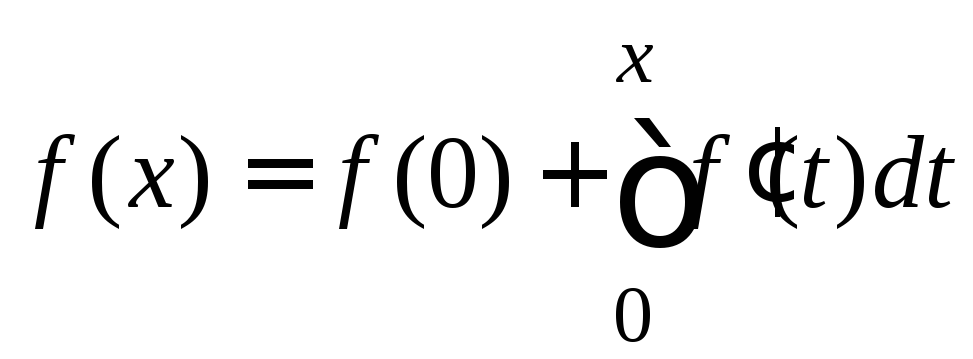 .
Отсюда существуют пределы
.
Отсюда существуют пределы![]() и
и![]() .
В силу абсолютной интегрируемости
.
В силу абсолютной интегрируемости![]() на всей прямой
на всей прямой![]() и
и![]() .
По определению преобразования Фурье
.
По определению преобразования Фурье

Ответ:
![]() .
.
Замечание.
Методом математической индукции можно
показать, что
![]() .
.
Пример. Найти преобразование Фурье от свертки.
Решение. По определению преобразования

Меняем порядок интегрирования
 .
.
Делаем
замену переменной
![]() .
Окончательно, получим
.
Окончательно, получим

т.е., также как в случае преобразования Лапласа, преобразование Фурье от свертки равно произведению преобразований Фурье.
Ответ:
![]() .
.
Косинус- преобразование и синус-преобразование Фурье
Пример.
Найти косинус-преобразование Фурье
функции
![]() (
(![]() ).
).
Решение. По определению косинус-преобразования Фурье
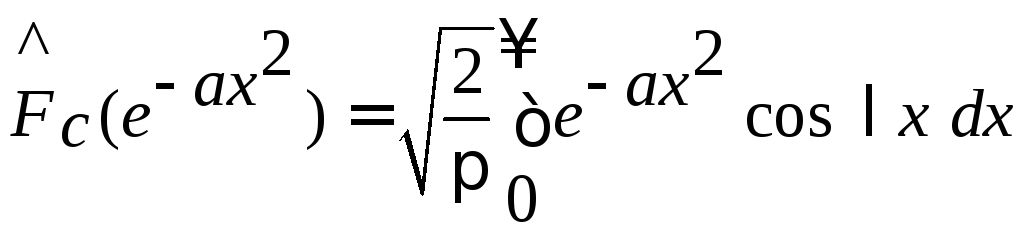 .
.
Так
как
![]() - четная функция, то
- четная функция, то ,
а
,
а .
Поэтому
.
Поэтому
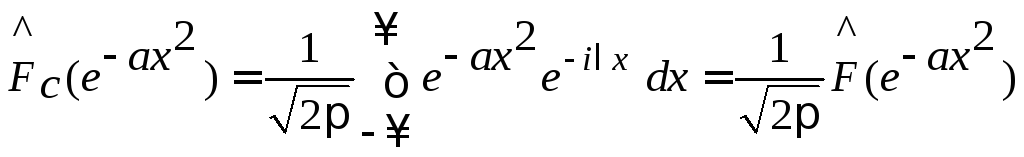 .
.
В примере было найдено
 .
.
Отсюда
 .
.
Ответ:
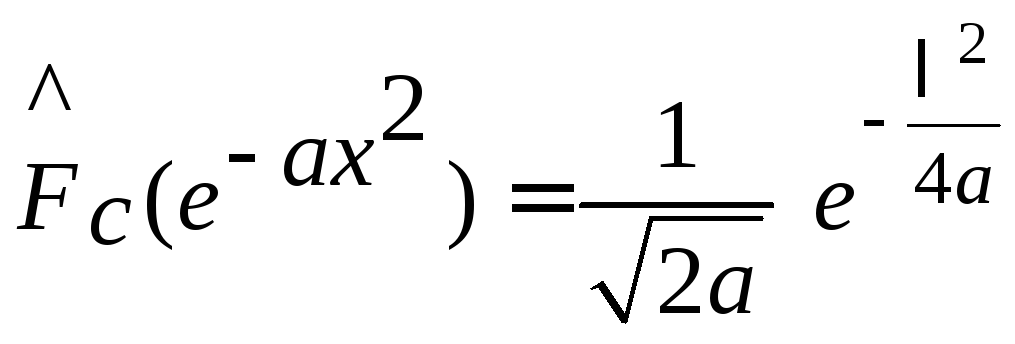 .
.
Пример.
Найти синус-преобразование Фурье функции
![]() (
(![]() ).
).
Решение. По определению синус-преобразования Фурье
 .
.
Используя формулу интегрирования по частям, преобразуем интеграл:

 .
.
Из результата первого примера получим
 .
.
Ответ:
 .
.
Задачи для самостоятельного решения
В задачах 11 - 13 представить указанные функции интегралом Фурье.
11.
![]() ;
;
12.
![]() .
.
13.
![]() .
.
В задачах 14 - 19 найти преобразование Фурье следующих функций.
14.
![]() ;
;
15.
![]() ;
;
16.
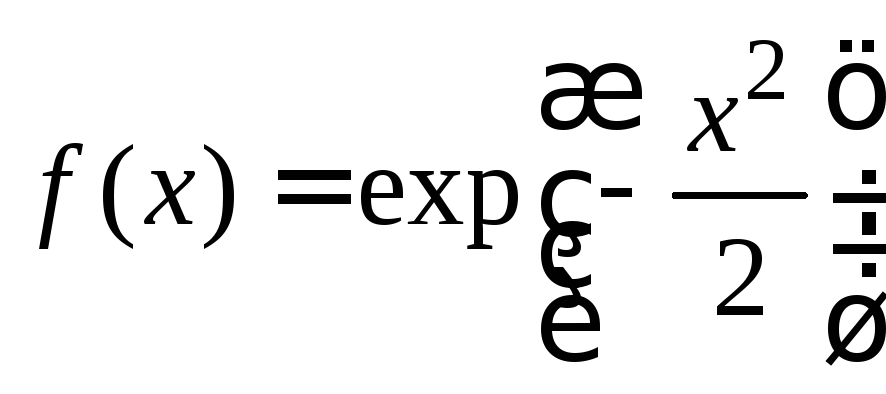 ,
где
,
где![]() ;
;
17.
![]() ;
;
18.
![]() ;
;
19.
![]() .
.
В
задачах 20 - 21
решить интегральное уравнение
 .
.
20.
![]() ;
;
21.
![]() .
.
Ответы
11.
 .
12.
.
12.
 .
13.
.
13.  .
14.
.
14.
![]() .
.
15.
![]() . 16.
. 16.
 .
.
17.
![]() .
18.
.
18.
![]() .
.
19. ![]() .
20.
.
20.
![]() .21.
.21.
![]() .
.
