
- •Модуль 7
- •Необходимое условие сходимости ряда
- •Задачи для самостоятельного решения
- •Знакочередующиеся ряды. Признак Лейбница
- •Условная сходимость. Признак Абеля-Дирихле
- •Задачи для самостоятельного решения
- •Занятие 10 Степенные ряды
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Занятия 12 Тригонометрический ряд Фурье функции на интервале
- •Ряд Фурье функции на интервале
- •Задачи для самостоятельного решения
- •Преобразование Фурье
- •Косинус- преобразование и синус-преобразование Фурье
- •Задачи для самостоятельного решения
Задачи для самостоятельного решения
В задачах 12 – 17 используя разложения элементарных функций, разложить в ряды Тейлора заданные функции и найти радиусы сходимости.
12.
![]() .
.
13. а) sin 2 z; б) cos 3 z.
14.
а)
![]() ; б)
; б)![]() .
.
15.
а)
![]() ; б)ln (2–z),
; б)ln (2–z),
![]() .
.
16.
а)
![]() ;
б)
;
б)![]() .
.
Указание: умножить и разделить на (z – 1);
17. а)
 ; б)
; б)![]() ; в)
; в)![]() .
.
18. С
помощью метода неопределенных
коэффициентов найти первые три отличные
от нуля члена разложения функций в ряд
Тейлора, полагая
![]()
а)
![]() ; б)
; б) .
.
В задачах 19 – 25 разложить функцию f(x) в степенной ряд и указать область его сходимости.
19.
![]() .20.
.20.
![]() .
.
21.
![]() . 22.
. 22.
![]() .
.
23.
 .24.
.24.
 .
.
25.
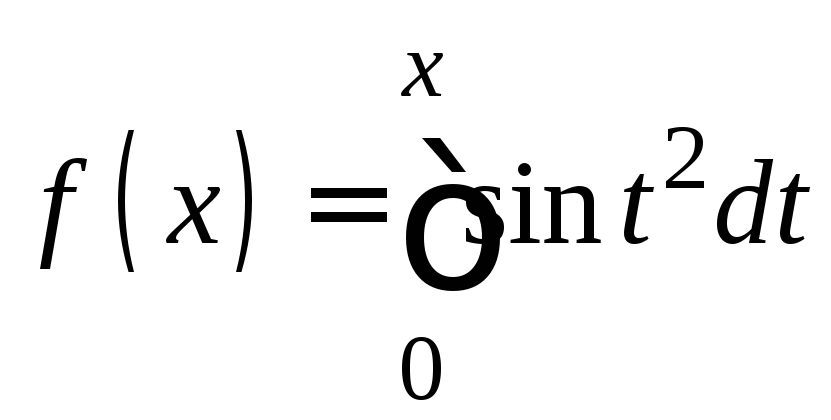 .
.
В задачах 26 – 29, представив функцию f(x) степенным рядом, вычислить интеграл.
26.
 .27.
.27.
 .
.
28.
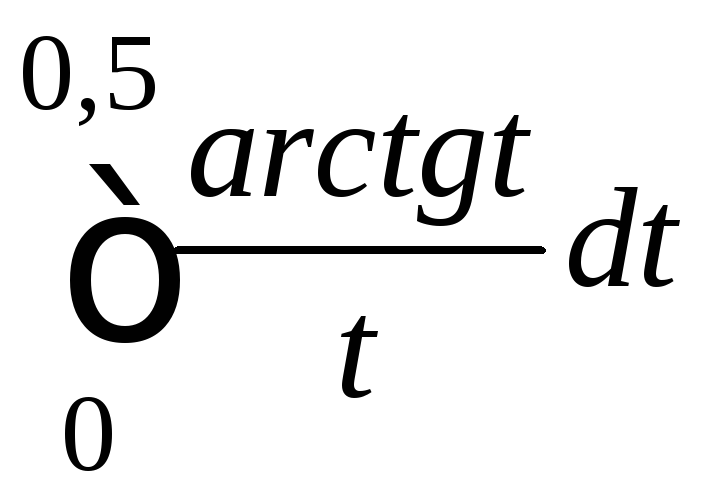 .
29.
.
29.
 .
.
В задачах 30 – 34, применив разложение в степенной ряд соответствующих функций, вычислить с точностью до 0,001.
30.
![]() . 31.
. 31.
![]() . 32.
. 32.
![]() .
.
33.
![]() .34. π.
.34. π.
В задачах 35 – 37 решить дифференциальные уравнения, представив искомую функцию в виде степенного ряда.
35.
![]() . 36.
. 36.
![]() . 37.
. 37.
![]() .
.
Разложить
функцию
![]() в ряд Тейлора.
в ряд Тейлора.
Указание.
Использовать тождество
![]() и применить формулу разложения
и применить формулу разложения![]() .
.
Ответы
12.
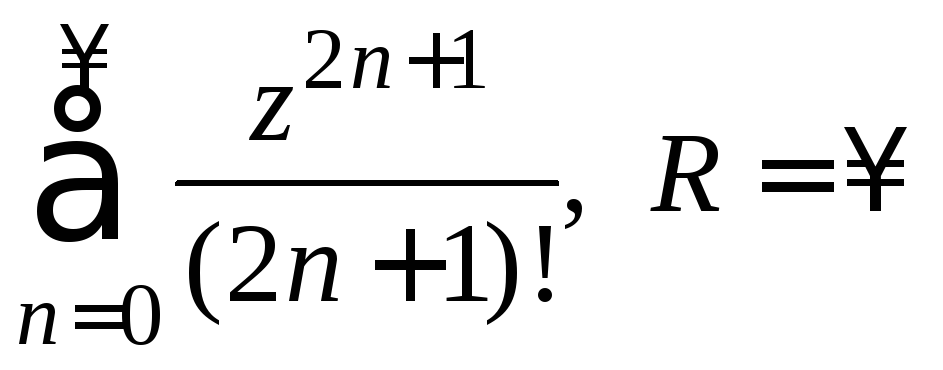 .
.
13.
а)
 б)
б) .
.
14. а)
 б)
б) .
.
15. а)
 б)
б) .
.
16. а)
 б)
б)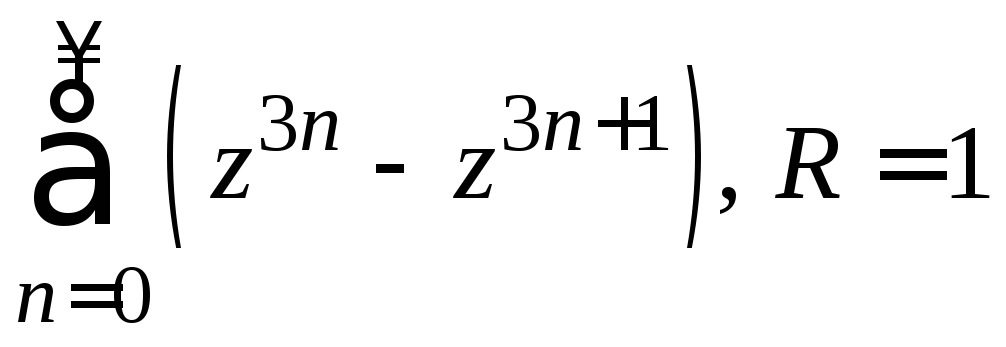 .
.
17.
а)
 б)
б)
в)
![]() .
.
18.
а)
![]() б)
б)![]()
19.
 ,
(−∞, +∞).20.
,
(−∞, +∞).20.
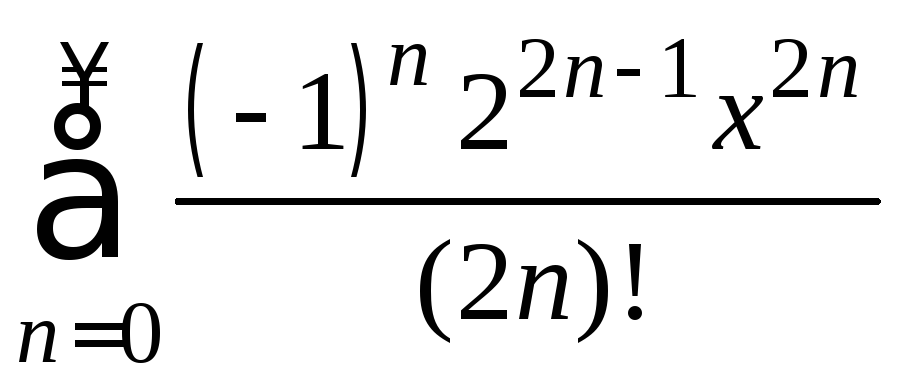 ,
(−∞, +∞).21.
,
(−∞, +∞).21.  ,
[−1, +1].22.
,
[−1, +1].22.
 ,
(−∞, +∞).
,
(−∞, +∞).
23.
 ,
(−∞, +∞).24.
,
(−∞, +∞).24.
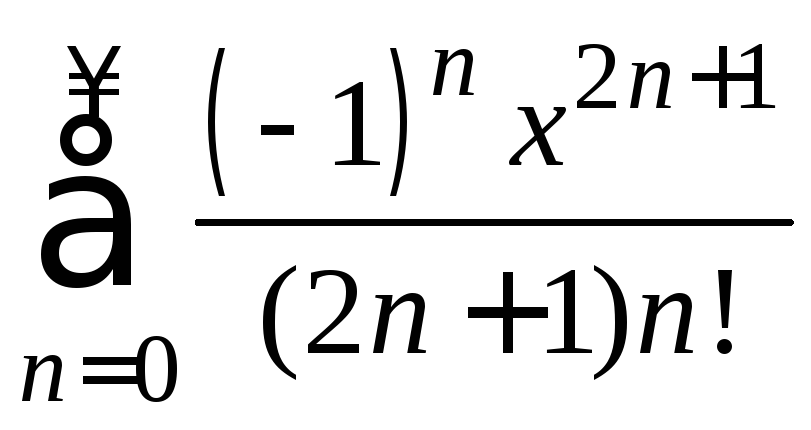 ,
(−∞, +∞).25.
,
(−∞, +∞).25.  ,
(−∞, +∞).26.
0,245. 27.
0,497. 28.
0,487.
,
(−∞, +∞).26.
0,245. 27.
0,497. 28.
0,487.
29. 0,006. 30. 0,368. 31. 0,342.
32.
0,693, применить формулу разложения
![]() с
с![]() .33.
3,107,
.33.
3,107,
![]() ,
применить формулу
,
применить формулу![]()
![]()
![]() .
.
34.
В формуле разложения
![]() положить
положить![]() .
.
35.  ,
(−∞, +∞).36.
,
(−∞, +∞).36.
![]() .37.
.37.
![]() .
.
Занятия 12 Тригонометрический ряд Фурье функции на интервале
Пример.
Разложить функцию
![]() в
тригонометрический ряд Фурье на интервале
в
тригонометрический ряд Фурье на интервале![]() .
.
Решение. Заметим, что
1)
интервал
![]() симметричный относительно начала
координат,
симметричный относительно начала
координат,
2)
функция
![]() четная.
четная.
Поэтому
в силу 1), 2) разложим по отдельности
каждое слагаемое функции
![]() в тригонометрический ряд Фурье на
интервале
в тригонометрический ряд Фурье на
интервале![]() .
.
Ряд
Фурье для 5 будет 5. Для функции
![]() в силу ее четности ряд Фурье совпадет
с разложением по косинусам. Вычисляем
в силу ее четности ряд Фурье совпадет
с разложением по косинусам. Вычисляем
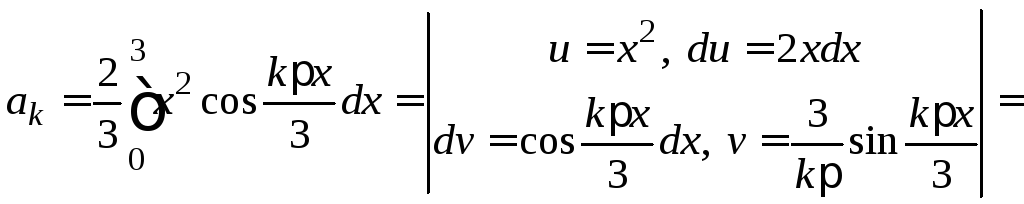

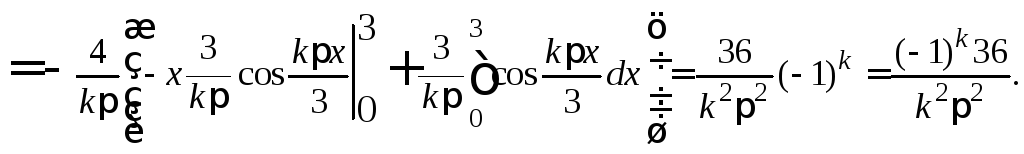
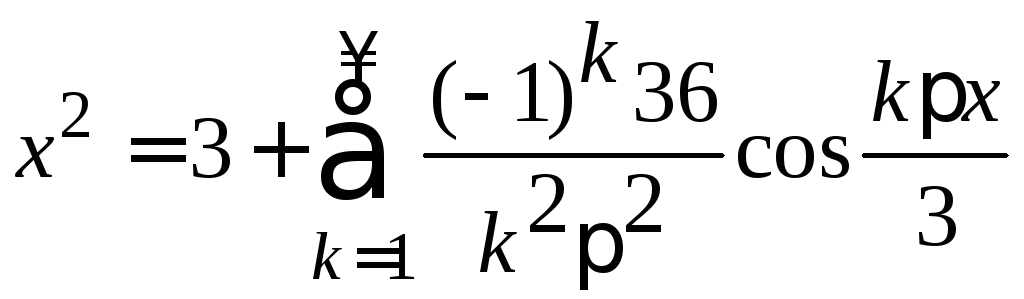 и
и
 .
.
О

 ,
,![]() .
.
Пример.
Разложить функцию
![]() в
тригонометрический ряд Фурье на интервале
в
тригонометрический ряд Фурье на интервале![]() (см. рис.).
(см. рис.).
Решение. Заметим, что
1)
интервал![]() симметричный относительно начала
координат,
симметричный относительно начала
координат,
2)
функция
![]() нечетная.
нечетная.
Поэтому
в силу 1), 2) разложим по отдельности
каждое слагаемое функции
![]() в тригонометрический ряд Фурье на
интервале
в тригонометрический ряд Фурье на
интервале![]() .
.
Ряд
Фурье для 2 будет 2. Для функции
![]() в силу ее нечетности ряд Фурье совпадет
с разложением по синусам. Вычисляем
в силу ее нечетности ряд Фурье совпадет
с разложением по синусам. Вычисляем
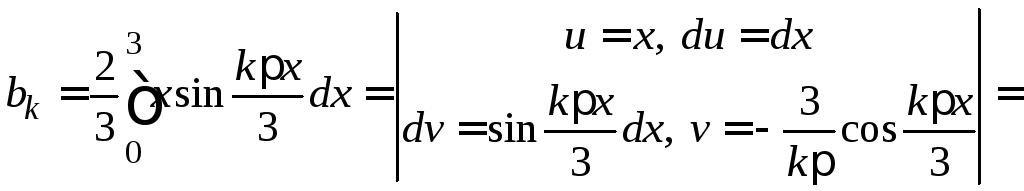

Ряды Фурье имеют вид:
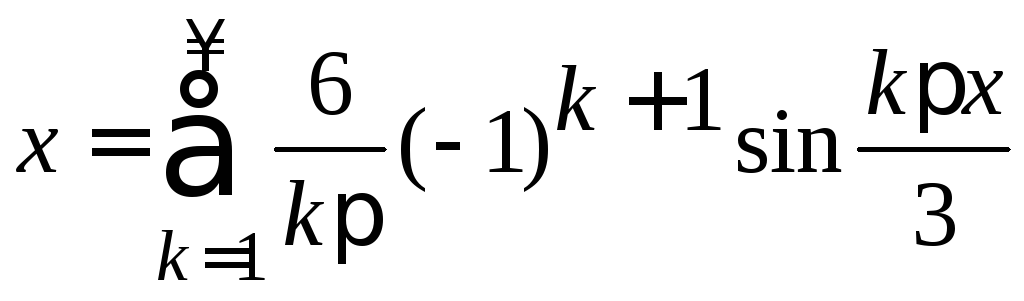 и
и
 .
.
Ответ:
 ,
,![]() .
.
Ряд Фурье функции на интервале
Ряд
Фурье функции
![]() на интервале
на интервале![]() определяется не однозначно, в частности,
а) по системе
определяется не однозначно, в частности,
а) по системе![]() ;
б) по системе
;
б) по системе![]() .
.
В
случае а) функция
![]() продолжается на симметричный интервал
как четная функция. Поэтому вычисляются
только
продолжается на симметричный интервал
как четная функция. Поэтому вычисляются
только![]()
![]() по формулам
по формулам
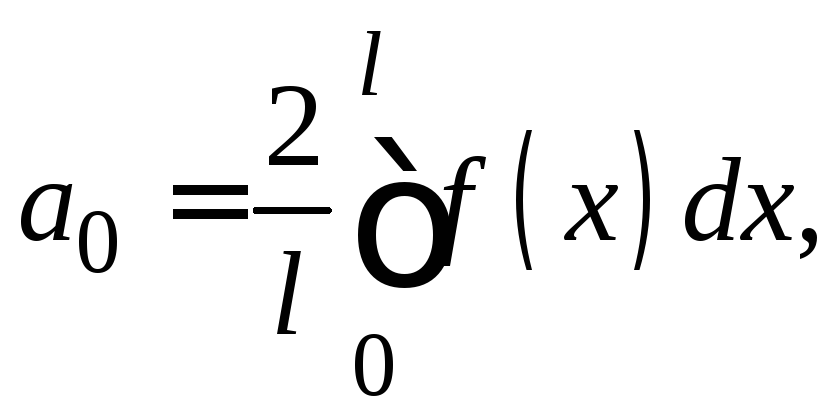
 .
.
В
случае б) функция
![]() продолжается на симметричный интервал
как нечетная функция. Поэтому вычисляются
только
продолжается на симметричный интервал
как нечетная функция. Поэтому вычисляются
только![]() по формуле
по формуле .
.
Пример.
Разложить функцию
![]() в
тригонометрический ряд Фурье на интервале
в
тригонометрический ряд Фурье на интервале![]() а) по системе
а) по системе![]() ;
;
б)
по системе
![]() .
.
Р

![]() четная функция на интервале
четная функция на интервале![]() .
Поэтому решаем случай б), когда функция
продолжена нечетным образом (см. рис.).
Вычисляем
.
Поэтому решаем случай б), когда функция
продолжена нечетным образом (см. рис.).
Вычисляем




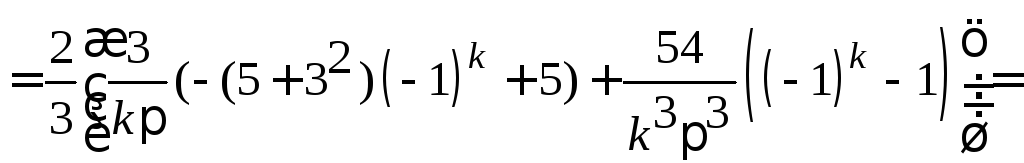
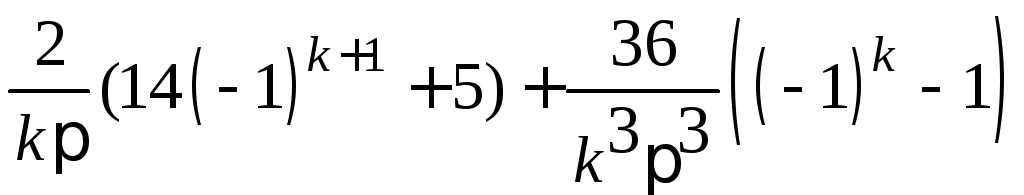 .
.
Ответ:
а)
 ,
,![]() ;
б)
;
б) 
Пример.
Разложить функцию
![]() в
тригонометрический ряд Фурье на интервале
в
тригонометрический ряд Фурье на интервале![]() а) по системе
а) по системе![]() ;
б) по системе
;
б) по системе![]() .
.
Р
Рис.
6.2.2.
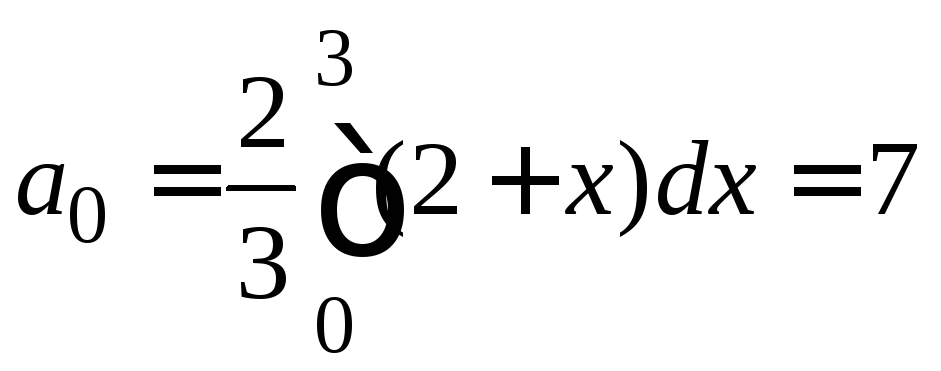 ,
,

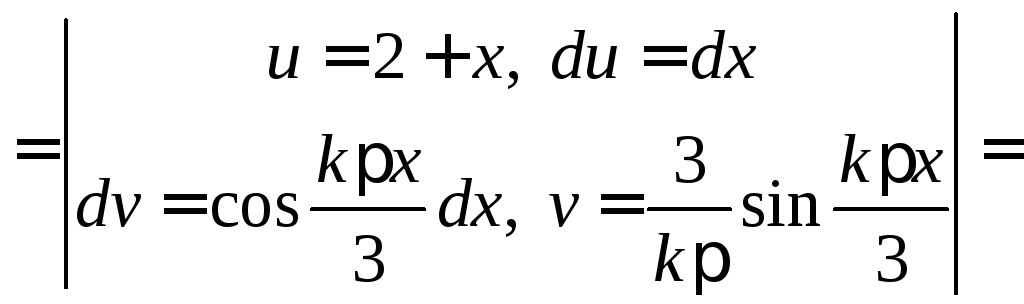


 .
.
Отсюда
 ,
,![]() .
.
б) Функция продолжена нечетным образом. Поэтому вычисляем только
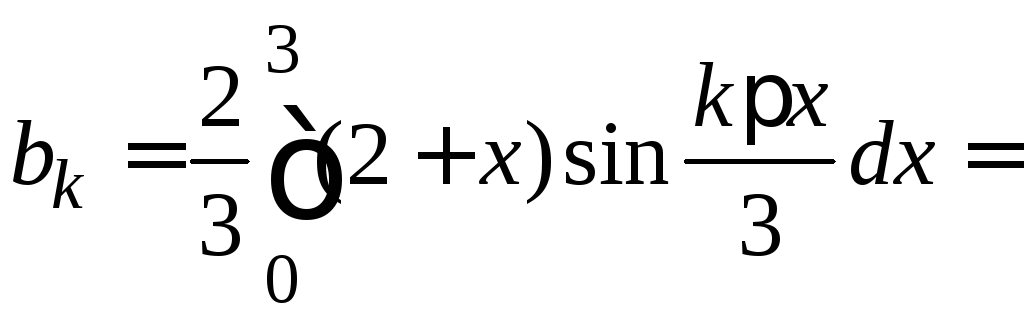


Отсюда
 .
.

Ответ:
а)  ,
,![]() ;
б)
;
б)
