Занятие 10 Степенные ряды

Пример. Найти область абсолютной сходимости ряда 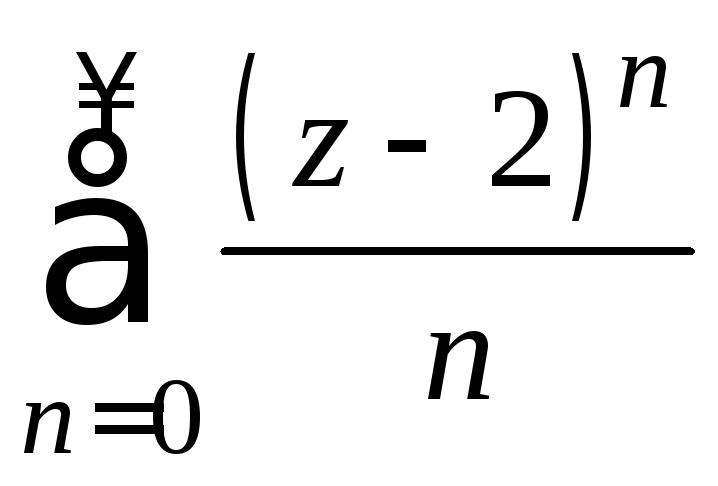. В каком круге рядравномерно сходится?

Решение. Выполним замену переменной . Тогда ряд примет вид

.

Составим ряд из модулей 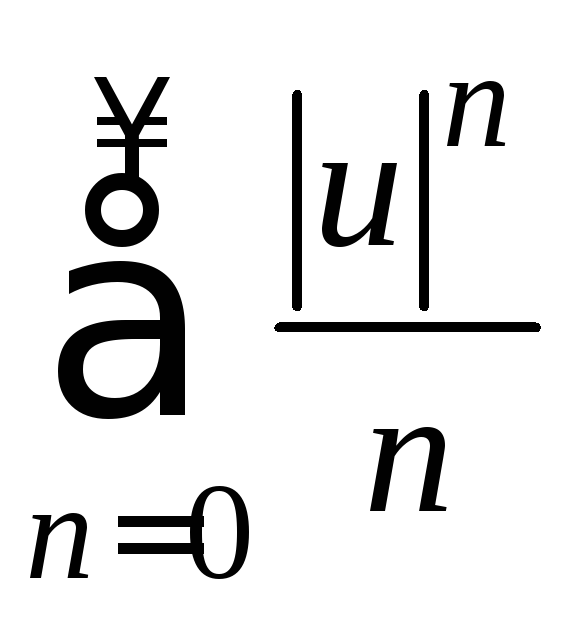, к которому применим признак Даламбера. Для этого найдем

.

По признаку Даламбера ряд абсолютно сходится, если . Отсюда радиус сходимости степенного ряда равен. Исследуем абсолютную сходимость на границе круга сходимости. Если, то ряд- это гармонический ряд, который, как известно, расходится. Поэтому по теореме Абеля ряд равномерно сходится. Заметим, что прирядсходится, на основании признака Абеля - Дирихле (полагая()), а

, .

Возвращаясь к исходной переменной, запишем ответ.

Ответ: абсолютно сходится,равномерно сходится.

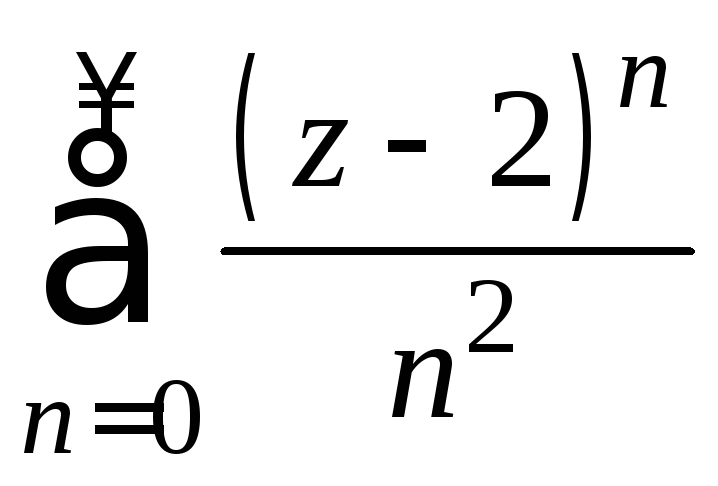Пример. Найти область абсолютной сходимости. В каком круге рядравномерной сходится?

Решение. Выполним замену переменной . Тогда ряд примет вид

.

Составим ряд из модулей , к которому применим признак Даламбера. Для этого найдем

.

По признаку Даламбера ряд абсолютно сходится, если . Отсюда радиус сходимости степенного ряда равен. Исследуем абсолютную сходимость на границе круга сходимости. Если, то ряд- это сходящийся ряд Дирихле. Поэтому по признаку Вейерштрасса ряд равномерно сходится. Возвращаясь к исходной переменной, запишем ответ.

Ответ: абсолютно и равномерно сходится.

Задачи для самостоятельного решения

В задачах 1 - 4 найти область абсолютной сходимости ряда . В каком круге рядравномерно сходится?

1. ;2. ;

3. ;4. .

В задачах 5 - 11 вычислив радиус R, найти область сходимости степенного ряда .

5. . 6. .

7. . 8. .

9. .10. .

11. .

Ответы

1. На всей комплексной плоскости сходится абсолютно и при равномерно сходится.2. На всей комплексной плоскости сходится абсолютно и при равномерно сходится.3. абсолютно сходится,равномерно сходится.4. абсолютно и равномерно сходится.5. [–1, 1). 6. (–1, 1] .

7. (–1/c, 1/c). 8. [–1/e, 1/e). 9. [–1, 1). 10. (–∞, ∞). 11. (–2, 2).

Ряды Тейлора

Используя разложения основных элементарных функций, а также возможность почленного дифференцирования и интегрирования степенных рядов, можно найти разложение некоторых функций по степеням .

Пример. Используя разложение , а также возможность почленного интегрирования степенных рядов, разложить функцию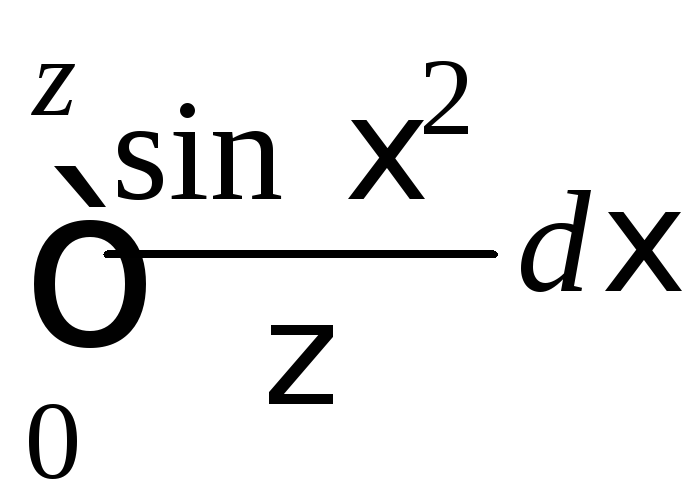по степенями указать область сходимости полученного ряда.

Решение. Как известно, . Поэтому

,

следовательно,

.

Отсюда

.

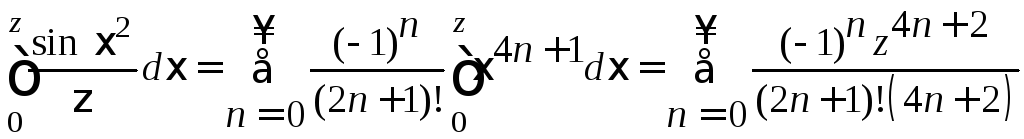Область сходимости для полученного ряда как и для разложения в ряд – вся комплексная плоскость, т.е. .

Ответ: , .

Пример. Разложить в ряд Тейлора в окрестности точки функцию. Найти радиус сходимости ряда.

Решение. Разложим данную функцию на элементарные дроби методом неопределенных коэффициентов:

.

Из тождества , полагая последовательно, находим

т.е.

.

Преобразуем правую часть равенства следующим образом:

.

Используя разложение функции , получим

Радиус сходимости можно определить двумя способами. Ряд в первой скобке сходится в круге , ряд во второй скобке в круге. Оба ряда сходятся в круге, поэтому радиус сходимостиR=1.

Второй способ определения R следует из формулы для

.

Радиус сходимости R равен расстоянию от центра круга до ближайшей точкипри которой знаменатель обращается в нуль. В нашем случае, а точка. Поэтому радиус сходимости равен

.

Ответ: , радиус сходимостиR=1.

Пример. Разложить в ряд Тейлора в окрестности точки функцию.

Решение. Преобразуем данную функцию следующим образом:

.

Используя разложение для получим.

Ряд сходится в круге .

Ответ: Ряд сходится в круге.

При разложении в ряды Тейлора отношения двух функций, ряды Тейлора которых известны, полезно применять метод неопределенных коэффициентов. Суть метода рассмотрим на конкретном примере. Теоретической основой метода является единственность разложения функции в ряд Тейлора.

Пример. С помощью метода неопределенных коэффициентов найти первые три отличные от нуля члена разложения функции f(z) = tg z в окрестности точки z = 0.

Решение. . По методу неопределенных коэффициентов, справедливо равенство.

Здесь ,…- неопределенные коэффициенты.

Так как функция tg z, нечетная, то .

Учитывая известные разложения для функций sinz, cosz получим тождество:

.

После преобразований, приравнивая коэффициенты при одинаковых степенях z, получим уравнения для неизвестных коэффициентов :

Решая эту систему, получим

.

Ответ:.