
Zadachi_2
.docxЗадача 1.1
Трейдер відкрив коротку позицію за опціоном call на акцію зі страйком $57, отримавши $7 премії. Яким буде його фінансовий результат, якщо на момент експірації ціна акції становитиме а) $30; б) $40; в) $50; г) $70; д) $100;? Побудуйте графік фінансового результату за опціонною позицією.
S=57$, П=7$, ТБ=страйк+премія=57+7=64$
call короткий, продавець отримав премію. мав зобов’язання продати страйк 57, а на ринку (30,40..)
|
C |
Пр |
SC |
ФР |
|
30 |
+7 |
0 |
+7 |
|
40 |
+7 |
0 |
+7 |
|
50 |
+7 |
0 |
+7 |
|
70 |
+7 |
-13 |
-6 |
|
100 |
+7 |
-43 |
-36 |
Max ФР=7$ віднімаємо від страйку результат (міг би продати по70, а продає по 57). Трейдер буде намагатися закрити позицію до точки беззбитковості.
Задача 1.2
Ціна спот на пшеницю становить $240. 5-місячна безризикова ставка 7% річних, а витрати на зберігання 8%. Розрахуйте ф’ючерсну ціну пшениці за умови, що споживча дохідність (дохід від зручності) становить 5%. Як та скільки може заробити арбітражер за ціни ф’ючерсу $245?
S=240$, r=7%, u=8%, c=5%, F=245$, T=5/12
F0=S0*e(r+u-c)*T
F0=240*e(0,07+0,08-0,05)*5/12=250,21$
Якщо через 5 місяців ціна буде 245$, то
250,21-245=5,21$ заробіток у майбутньому, якщо купити ф’ючерс зараз (дохід від зручності знижує форвардну ціну)
Задача 1.3
Трейдер відкрив довгу позицію за опціоном call на акцію зі страйком $140, сплативши $13 премії. Яким буде його фінансовий результат, якщо на момент експірації ціна акції становитиме а) $100; б) $130; в) $145; г) $160; д) $180? Побудуйте графік фінансового результату за опціонною позицією.
S=140$, П=13$, ТБ=страйк+премія=140+13=153$
|
С |
Пр |
LC |
ФР |
|
100 |
-13 |
0 |
-13 |
|
130 |
-13 |
0 |
-13 |
|
145 |
-13 |
+5 |
-8 |
|
160 |
-13 |
+20 |
+7 |
|
180 |
-13 |
+40 |
+27 |
Прибуток необмежений
Задача 1.4
Ціна акції на ринку спот $160, компанія кожного кварталу виплачує $4 дивідендів. 3-місячна безризикова ставка знаходиться на рівні 8% річних. Якою є теоретична ціна 3-місячного форвардного контракту? Як та скільки може заробити арбітражер за ціни форварду $170?
S0=160$, d=4$ (щоквартально), T=3/12, r=8%
F0=(S0–d)*ert
F0=(160–4)*e0,08*3/12=159,15$
Якщо купити за 170$, а реалізувати за 159,15$, то збиток = - 10,85$
Треба купити акцію, продати форвард бо принесе < ніж є на сьогодні. Купити БА, продати форвард.
Задача 1.5
Трейдер відкрив довгу позицію за опціоном put на акцію зі страйком $156, сплативши $14 премії. Яким буде його фінансовий результат, якщо на момент експірації ціна акції становитиме а) $110; б) $130; в) $154; г) $168; д) $250? Побудуйте графік фінансового результату за опціонною позицією.
S=156$, П=14$, ТБ=страйк-премія=156-14=142$
|
С |
Пр |
LP |
ФР |
|
110 |
-14 |
+46 |
+32 |
|
130 |
-14 |
+26 |
+12 |
|
154 |
-14 |
+2 |
-12 |
|
168 |
-14 |
0 |
-14 |
|
250 |
-14 |
0 |
-14 |
Якщо ціна > ціни страйк опціон виконуватись не буде. Сплатити премію, купити опціон. Премія = max витрати. Чим нижча ціна, тим більше він заробить.
Задача 1.6
Ціна на бездивідендну акцію на ринку спот встановилась на рівні $120, а 3-місячні форвардні контракти укладаються за ціною $122. Чи може арбітражер заробити в даній ситуації, якщо відповідна безризикова ставка становить 8% річних? Якщо так, то скільки і яким чином?
S0=120$, F=122$, T=3/12, r=8%
F0=S0*ert
F0=120*e0,08*3/12=122,42$
Задача 1.7
Трейдер відкрив довгу позицію за опціоном call зі страйком $60 та премією $9. За яких умов дана стратегія принесе прибуток? За яких умов буде збиток? Якою є точка беззбитковості? Якими будуть максимальний прибуток та збиток? Побудуйте графік.
ТБ=60+9=69
Прибуток необмежений
Max збиток = 9$
Прибуток якщо Ціна > 69
Збиток якщо Ціна < 69
Задача 1.8
Ціна акції на ринку спот $90, а її дивідендна дохідність 2%. 6-місячна безризикова ставка знаходиться на рівні 6% річних. Якою є теоретична ціна 6-місячного форвардного контракту? Як та скільки може заробити арбітражер за ціни форварду $98?
S=90$, q=2%, r=6%, F=98$, T=6/12
F0=S0*e(r-q)*T
F0=90*e(0,06-0,02)*6/12=91,806$
або
q=m*ln(1+(Rm/m))=2*ln(1+(0,02/2))=0,0199
F0=90*e(0,06-0,0199)*0,5=98,71$
Свідчить, що F зараз=98$. Продати форвард, купити акцію за ціною S.
Краще купити зараз, інакше збиток сягатиме 98-91,806=6,194$
Задача 1.9
Трейдер відкрив коротку позицію за опціоном put на акцію зі страйком $240, отримавши $20 премії. Яким буде його фінансовий результат, якщо на момент експірації ціна акції становитиме а) $150; б) $200; в) $240; г) $270; д) $350? Побудуйте графік фінансового результату за опціонною позицією.
S=240$, П=20$, ТБ=страйк-премія=240-20=220$
|
С |
Пр |
SP |
ФР |
|
150 |
+20 |
-70 |
-50 |
|
200 |
+20 |
-40 |
-20 |
|
240 |
+20 |
0 |
+20 |
|
270 |
+20 |
0 |
+20 |
|
350 |
+20 |
0 |
+20 |
Якщо ціна<240 -> втрати
Ціна знижується -> втрати
Задача 1.10
7-місячні ф’ючерси на сою торгуються по $1300, в той час як ціна спот становить $1360. 7-місячна безризикова ставка знаходиться на рівні 6% річних, а витрати на зберігання – 5%. Якою має бути споживча дохідність (дохід від зручності) за даних умов?
u=5%, T=7/12, r=6%, S=1360, Ціна = 1300
F0=S0*e(r+u-q)*T
F0=1360*e(0,06+0,05-0,18733)*7/12=1300,015$
F0=S0*e(r-q)*T
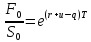
1300/1360=e(0,06+0,05-q)*7/12
ln 0,95588= ln e(0,11-q)*7/12
-0,04512=(0,11-q)*7/12
-0,0773=0,11-q
q (дивідендна дохідність)=0,18733
Задача 2.1
Страйк європейського опціону call на бездивідендну акцію становить $80, а ціна акції $81. Безризикова ставка дорівнює 9%. Час до погашення опціону – 2 місяці. Річна волатильність акції становить 25%. Розрахуйте вартість опціону, використавши модель Блека-Шоулза або двокрокову біноміальну модель.
K=80$, S0=81$, r=9%, T=2/12, σ=25%
C=S0*N(d1)-K*e-rT*N(d2)
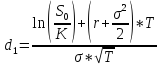
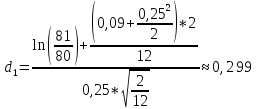
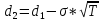
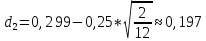
N(d1)=0,6141, N(d2)=0,5753
C=81*0,6141-80*e-0,09*2/12*0,5753=4,4$
Задача 2.2
Трейдер продав опціон call на цукор зі страйком 2000 грн. та премією 140 грн. Також він продав опціон put на цукор зі страйком 2000 грн. та премією 140 грн. Визначити фінансовий результат стратегії, якщо на момент експірації ціна базового активу становитиме: а) 1500 грн.; б) 1750 грн.; в) 2000 грн.; г) 2250 грн.; д) 2500 грн. Побудувати графік функції виплат на момент експірації, позначивши страйки та точки беззбитковості.
S. Call 2000/140
S. Put 2000/140
ТБ1=2000-280=1720
ТБ2=2000+280=2280
|
C |
Пр |
SC |
SP |
ФР |
|
1500 |
+280 |
0 |
-500 |
-220 |
|
1750 |
+280 |
0 |
-250 |
+30 |
|
2000 |
+280 |
0 |
0 |
+280 |
|
2250 |
+280 |
-250 |
0 |
+30 |
|
2500 |
+280 |
-500 |
0 |
-220 |
Задача 2.3
Страйк європейського опціону put на бездивідендну акцію становить $150, а ціна акції $155. Безризикова ставка дорівнює 10%. Час до погашення опціону – 4 місяці. Річна волатильність акції становить 20%. Розрахуйте вартість опціону, використавши модель Блека-Шоулза або двокрокову біноміальну модель.
K=150$, S0=155$, r=10%, T=4/12, σ=20%
P=K*e-rT*N(-d2)-S0*N(-d1)
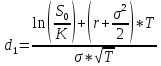
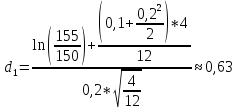
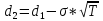
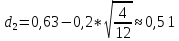
N(-d1)=0,7357
N(-d2)=0,6950
P=150*e-0,1*4/12*(1-0.6950)-155*(1-0.7357)=3.28$
Задача 2.4
Трейдер придбав опціон call на сталь зі страйком 500 грн. та премією 20 грн. Також він придбав опціон put на сталь зі страйком 400 грн. та премією 50 грн. Визначити фінансовий результат стратегії, якщо на момент експірації ціна базового активу становитиме: а) 250 грн.; б) 350 грн.; в) 450 грн.; г) 550 грн; д) 650 грн. Побудувати графік функції виплат на момент експірації, позначивши страйки та точки беззбитковості.
ТБ1=330, ТБ2=570
|
C |
Пр |
SC |
SP |
ФР |
|
250 |
-70 |
0 |
+150 |
+80 |
|
350 |
-70 |
0 |
+50 |
-20 |
|
450 |
-70 |
0 |
0 |
-70 |
|
550 |
-70 |
+50 |
0 |
-20 |
|
650 |
-70 |
+150 |
0 |
+80 |
Задача 2.5
Страйк європейського опціону call на бездивідендну акцію становить $120, а ціна акції $130. Безризикова ставка дорівнює 5%. Час до погашення опціону – 2 місяці. Річна волатильність акції становить 25%. Розрахуйте вартість опціону, використавши модель Блека-Шоулза або двокрокову біноміальну модель.
K=120$, S0=130$, r=5%, T=2/12, σ=25%
C=S0*N(d1)-K*e-rT*N(d2)
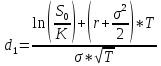
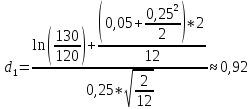
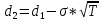
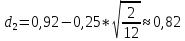
N(d1)=0,8212, N(d2)=0,7939
C=130*0,8212-120*e-0,05*2/12*0,7939=12,28$
Задача 2.6
Трейдер придбав опціон call на каву зі страйком 700 грн. та премією 50 грн. Також він продав опціон call на каву зі страйком 750 грн. та премією 30 грн. Визначити фінансовий результат стратегії, якщо на момент експірації ціна базового активу становитиме: а) 600 грн.; б) 700 грн.; в) 800 грн.; г) 900 грн; д) 1000 грн. Побудувати графік функції виплат на момент експірації, позначивши страйки та точки беззбитковості.
L. Call 700/50
S. Call 750/50
ТБ=720
|
C |
Пр |
SC |
SP |
ФР |
|
600 |
-20 |
0 |
0 |
-20 |
|
700 |
-20 |
0 |
0 |
-20 |
|
800 |
-20 |
+100 |
-50 |
+30 |
|
900 |
-20 |
+200 |
-150 |
+30 |
|
1000 |
-20 |
+300 |
-250 |
+30 |
Задача 2.7
Страйк європейського опціону put на бездивідендну акцію становить $200, а ціна акції $190. Безризикова ставка дорівнює 5%. Час до погашення опціону – 2 місяці. Річна волатильність акції становить 25%. Розрахуйте вартість опціону, використавши модель Блека-Шоулза або двокрокову біноміальну модель.
K=200$, S0=190$, r=5%, T=2/12, σ=25%
P=K*e-rT*N(-d2)-S0*N(-d1)
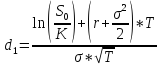
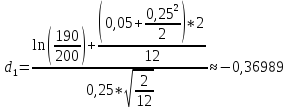
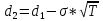
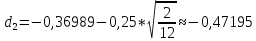
N(-d1)=0,6443
N(-d2)=0,6808
P=200*e-0,05*2/12*0.6808-190*0.6443=12.61$
Задача 2.8
Трейдер придбав опціон call на ф’ючерс зі страйком 1200 грн. та премією 50 грн. Також він придбав 2 опціони put на ф’ючерс зі страйком 1200 грн. та премією 51 грн. Визначити фінансовий результат стратегії, якщо на момент експірації ціна базового активу становитиме: а) 800 грн.; б) 1000 грн.; в) 1200 грн.; г) 1400 грн; д) 1600 грн. Побудувати графік функції виплат на момент експірації, позначивши страйки та точки беззбитковості.
ТБв=1200+50+2*51=1352
ТБн=1200-((50+2*51)/2)=1124
|
C |
Пр |
SC |
SP |
ФР |
|
800 |
-152 |
0 |
+800 |
+648 |
|
1000 |
-152 |
0 |
+400 |
+248 |
|
1200 |
-152 |
0 |
0 |
-152 |
|
1400 |
-152 |
+200 |
0 |
+48 |
|
1600 |
-152 |
+400 |
0 |
+248 |
Задача 2.9
Страйк європейського опціону call на бездивідендну акцію становить $60, а ціна акції $55. Безризикова ставка дорівнює 3%. Час до погашення опціону – 4 місяці. Річна волатильність акції становить 30%. Розрахуйте вартість опціону, використавши модель Блека-Шоулза або двокрокову біноміальну модель.
K=60$, S0=55$, r=3%, T=4/12, σ=30%
C=S0*N(d1)-K*e-rT*N(d2)
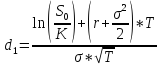
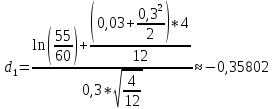
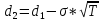
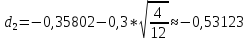
N(d1)=0,6406
N(d2)=0.7019
C=55*(-0.6406)-60*e-0,03*4/12*(1-0.7019)=2.06$ - вартість опціону call
Задача 2.10
Трейдер придбав опціон call на кукурудзу зі страйком 2500 грн. та премією 200 грн. Також він придбав опціон put на кукурудзу зі страйком 2500 грн. та премією 205 грн. Визначити фінансовий результат стратегії, якщо на момент експірації ціна базового активу становитиме: а) 1500 грн.; б) 2000 грн.; в) 2500 грн.; г) 3000 грн; д) 3500 грн. Побудувати графік функції виплат на момент експірації, позначивши страйки та точки беззбитковості.
ТБ=2095
|
C |
Пр |
SC |
SP |
ФР |
|
1500 |
-405 |
0 |
+1000 |
+595 |
|
2000 |
-405 |
0 |
+500 |
+95 |
|
2500 |
-405 |
0 |
0 |
-405 |
|
3000 |
-405 |
+500 |
0 |
+95 |
|
3500 |
-405 |
+1000 |
0 |
+595 |
Задача 2.11
Страйк європейського опціону put на бездивідендну акцію становить $180, а ціна акції $170. Безризикова ставка дорівнює 5%. Час до погашення опціону – 4 місяці. Річна волатильність акції становить 20%. Розрахуйте вартість опціону, використавши модель Блека-Шоулза або двокрокову біноміальну модель.
K=180$, S0=170$, r=5%, T=4/12, σ=20%
P=K*e-rT*N(-d2)-S0*N(-d1)
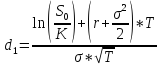
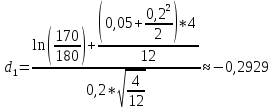
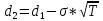
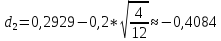
N(-d1)=0,6141
N(-d2)=0,6591
P=180*e-0,05*4/12*(1-0.6591)-170*(1-0.6141)=12.28$
Задача 2.12
Трейдер продав опціон put на пшеницю зі страйком 1000 грн. та премією 30 грн. Також він купив опціон put на пшеницю зі страйком 1100 грн. та премією 85 грн. Визначити фінансовий результат стратегії, якщо на момент експірації ціна базового активу становитиме: а) 850 грн.; б) 950 грн.; в) 1050 грн.; г) 1150 грн; д) 1250 грн. Побудувати графік функції виплат на момент експірації, позначивши страйки та точки беззбитковості.
S. Put 1000/30
L. Put 1100/85
|
C |
Пр |
SC |
SP |
ФР |
|
850 |
-55 |
-150 |
+250 |
+45 |
|
950 |
-55 |
-50 |
+150 |
+45 |
|
1050 |
-55 |
0 |
50 |
-5 |
|
1150 |
-55 |
0 |
0 |
-55 |
|
1250 |
-55 |
0 |
0 |
-55 |
Білет №9
4. 5-місячні ф’ючерси на пшеницю торгуються по $200, в той час як ціна спот становить $210. 6-місячна безризикова ставка знаходиться на рівні 5% річних, а витрати на зберігання – 7%. Якою має бути споживча дохідність (дохід від зручності) за даних умов?
u=7%, T=5/12, r=5%, S=210, Ціна = 200
F0=S0*e(r+u-q)*T
F0=210*e(0,05+0,07-0,2371)*5/12=199,9997$
F0=S0*e(r-q)*T
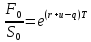
200/210=e(0,05+0,07-q)*5/12
ln 0,95238= ln e(0,12-q)*5/12
-0,04879=(0,12-q)*5/12
-0,1171=0,12-q
q (дивідендна дохідність)=0,2371
5. Трейдер купив опціон call на цукор зі страйком 2200 грн. та премією 160 грн. Також він купив опціон put на цукор зі страйком 2200 грн. та премією 160 грн. Визначити фінансовий результат стратегії, якщо на момент експірації ціна базового активу становитиме: а) 1750 грн.; б) 2000 грн.; в) 2250 грн.; г) 2500 грн; д) 2750 грн. Побудувати графік функції виплат на момент експірації, позначивши страйки та точки беззбитковості.
1 L. Call 2200/160
1 L. Put 2200/160
Long Straddle
Премія = 160+160=320
ТБв=2200+320=2520
ТБн=2200-320=1880
|
C |
Пр |
LC |
LP |
ФР |
|
1750 |
-320 |
0 |
+450 |
+130 |
|
2000 |
-320 |
0 |
+200 |
-120 |
|
2250 |
-320 |
+50 |
0 |
-270 |
|
2500 |
-320 |
+300 |
0 |
-20 |
|
2750 |
-320 |
+550 |
0 |
+230 |
Опціон, негайна реалізація якого приносить прибуток, називається:
опціоном «з грошима»
Угода між двома сторонами про періодичний обмін грошовими потоками у майбутньому – це:
своп
Якщо ринкова ціна базового активу значно більша, ніж страйк опціону call, цей опціон перебуває:
з грошима (ITM)
Можливість того, що ремонті роботи призведуть до відсутності електроенергії в офісі компанії – це:
операційний ризик
На рахунку трейдера 5 000$. Ціна ф’ючерсу 2 000$, а гарантійне забезпечення за ним становить 10%. Максимальна кількість ф’ючерсів, яку може придбати трейдер:
2
Білет№10
4. Страйк європейського опціону call на бездивідендну акцію становить $70, а ціна акції $64. Безризикова ставка дорівнює 5%. Час до погашення опціону – 4 місяці. Річна волатильність акції становить 30%. Розрахуйте вартість опціону, використавши модель Блека-Шоулза або двокрокову біноміальну модель.
K=70$, S0=64$, r=5%, T=4/12, σ=30%
C=S0*N(d1)-K*e-rT*N(d2)
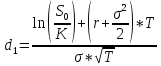
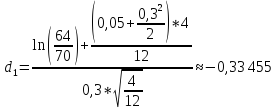
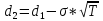
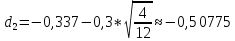
N(-d1)= 0.6293
N(-d2)= 0,6950
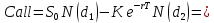 64*(1-0.6293)-70*е-0,05*4/12*(1-0.6950)=2,02$
64*(1-0.6293)-70*е-0,05*4/12*(1-0.6950)=2,02$
5. Трейдер придбав 2 опціони call на сою зі страйком 1500 грн. та премією 120 грн. Також він придбав опціон put на сою зі страйком 1500 грн. та премією 130 грн. Визначити фінансовий результат стратегії, якщо на момент експірації ціна базового активу становитиме: а) 1000 грн.; б) 1250 грн.; в) 1500 грн.; г) 1750 грн; д) 2000 грн. Побудувати графік функції виплат на момент експірації, позначивши страйки та точки беззбитковості.
2 L. Call 1500/120
1 L. Put 1500/130
Long Strap
Премія = 120*2+130=370
ТБв=1500+370/2=1685
ТБн=1500-370=1130
|
C |
Пр |
2LC |
LP |
ФР |
|
1000 |
-370 |
0 |
+500 |
+130 |
|
1250 |
-370 |
0 |
+250 |
-120 |
|
1500 |
-370 |
0 |
0 |
-370 |
|
1750 |
-370 |
+500 |
0 |
+130 |
|
2000 |
-370 |
+1000 |
0 |
+630 |
