Часть 3. Дискретные и непрерывные случайные величины. Законы распределения
Глава 1. Понятие случайной величины
В том случае, если случайное событие выражается в виде числа, можно говорить о случайной величине. Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Выпадение некоторого значения случайной величины Х это случайное событие: Х = хi. Среди случайных величин выделяют дискретные и непрерывные случайные величины.
Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.
Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.
Любая случайная величина имеет свой закон распределения вероятностей и свою функцию распределения вероятностей. Прежде, чем дать определение функции распределения, рассмотрим переменные, которые её определяют. Пусть задано некоторое х – действительное число и получена случайная величина X, при этом (x>X). Требуется определить вероятность того, что случайная величина Х будет меньше этого фиксированного значения х.
Функцией распределения случайной величины Х называется функция F(х), определяющая вероятность того, что случайная величина Х в результате испытания примет значение меньшее значения х, то есть:
F (х) = Р(Х < х ). |
(1.1) |
где х – произвольное действительное число.
Случайная величина (непрерывная или дискретная) имеет численные характеристики:
Математическое ожидание М (Х). Эту характеристику можно сравнивать со средним арифметическим наблюдаемых значений случайной величины Х.
Дисперсия D(X). Это характеристика отклонения случайной величины Х от математического ожидания.
Среднее квадратическое отклонение σ(Х) для дискретной и непрерывной случайной величины Х – это корень квадратный из ее дисперсии:
σ(x) = D(x) . |
(1.2) |
Далее рассматриваются отличия между дискретной и непрерывной случайными величинами.
Глава 2. Дискретная случайная величина
2.1. Закон распределения дискретной случайной величины
Рассмотрим дискретную случайную величину на примере.
20
Пример 1. Число появлений герба при трех бросаниях монеты является дискретной случайной величиной Х. Возможные значения числа появлений герба: 0,1,2,3. Следует найти вероятность появления герба в одном испытании. Решение. Вероятность появления герба в
p = |
1 |
|
|
2 . По формуле умножения для независимых событий: |
|||
одном испытании равна |
|||
1) Событие 1.Три раза бросили и ни разу герб не выпал. Для этого события вероятность:
P(0) = q1 q2 q3 = 213 = 18 .
2) Событие 2. Три раза бросили и один раз герб выпал. Для этого события вероятность события будет состоять из суммы событий:
P(1) = p1 q2 q3 + q1 p2 q3 + q1 q2 p3 = 18 + 18 + 18 = 83 .
3) Событие 3. Три раза бросили и два раза выпал герб. Для этого события вероятность события будет состоять из суммы событий:
P(2) |
= p p |
2 |
q |
3 |
+ q p |
2 |
p |
+ p q |
2 |
p |
3 |
= |
1 |
+ |
1 |
+ |
1 |
= |
3 |
|
|
|
|
|
|||||||||||||||||
|
1 |
|
1 |
|
1 |
|
8 |
8 |
8 |
8 . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4) Событие 4. Три раза бросили и все три раза выпал герб. Вероятность этого события совпадает с первым и вычисляется по формуле умножения.
P(3) = p1 p2 p3 = 213 = 18 .
Здесь: p1, p2, p3 – вероятность выпадения герба в 1, 2, 3 испытаниях. q1, q2, q3 – вероятность не выпадения герба в 1, 2, 3 испытаниях. Результаты вычислений вынесены в таблицу 1.
|
|
|
|
Таблица 1 |
|
|
|
|
|
|
|
Событие Х |
герб |
герб |
герб |
герб |
|
не выпал |
выпал 1 раз |
выпал 2 раза |
выпал 3 раза |
|
|
|
|
||||
|
|
|
|
|
|
хi |
0 |
1 |
2 |
3 |
|
Вероятность |
1 |
3 |
3 |
1 |
|
события: |
|
||||
8 |
8 |
8 |
8 |
|
|
Р(хi)= рi |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Законом распределения дискретной случайной величины называют соответствие между полученными значениями дискретной случайной величины и их вероятностями. Его можно задать:
1)таблично (рядом распределения);
2)графически;
3)аналитически (в виде формулы).
Впримере 1 закон распределения задан в виде ряда распределения (таблицей 1), где представлены все возможные значения хi и соответствующие им вероятности рi = Р ( Х = хi ).
n
∑pi =1
При этом вероятности рi удовлетворяют условию: i=1 , потому, что число возможных значений n может быть конечным или бесконечным.
n
∑(Х =xi ) = Ω
i=1 , где
21
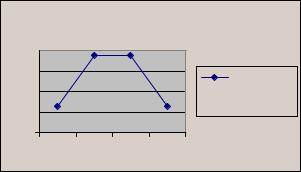
Графическое изображение ряда распределения называется многоугольником распределения. Для его построения возможные значения случайной величины (хi) откладываются по оси абсцисс, а вероятности (рi) – по оси ординат. Точки Аi c координатами (хi, рi) соединяются ломаными линиями.
Функция F(х) для дискретной случайной величины вычисляется по формуле:
F(x) = ∑pi |
(1.3) |
xi <x |
, |
|
где суммирование ведется по всем значениям i, для которых хi < х.
Пример 2. Для задачи в примере 1 найти функцию распределения вероятности F(х) этой случайной величины и построить ее. Построить многоугольник распределения.
Решение.
Если х ≤ 0, то F(х) = Р ( Х < х ) = 0.
Если 0 < х ≤ 1, то F(х) = Р ( Х < х ) = 1/8.
Если 1 < х ≤ 2, то F(х) = Р ( Х < х ) = 1/8 + 3/8 = 0,5. Если 2 < х ≤ 3, то F(х) = Р ( Х < х ) = 1/8 + 3/8 + 3/8 = 7/8. Если х > 3, то F(х) = Р ( Х < х ) = 1/8 + 3/8 + 3/8 + 1/8 = 1.
В таблицу 2 внесены значения функции распределения вероятности F(х) случайной величины – х.
Таблица 2
№ |
1 |
2 |
3 |
4 |
5 |
хi |
0 |
1 |
2 |
3 |
>3 |
|
|
|
|
|
|
функция распределения |
0 |
0,125 |
0,5 |
0,875 |
1 |
F(х) |
|
|
|
|
|
Для построения многоугольника распределения значения случайной величины х переписаны в другой форме из таблицы 1 в таблицу 3.
Таблица 3
№ |
1 |
2 |
3 |
4 |
хi |
0 |
1 |
2 |
3 |
Ряд распределения |
0,125 |
0,375 |
0,375 |
0,125 |
Р(хi)= рi |
|
|
|
|
Многоугольник распределения и полученная функция распределения вероятности представлены на рис. 1, 2.
Вероятность события : |
Р(хi)= рi |
|||
0,4 |
|
|
|
|
0,3 |
|
|
|
Вероятнос |
0,2 |
|
|
|
|
|
|
|
ть события |
|
0,1 |
|
|
|
: Р(хi)= рi |
|
|
|
|
|
0 |
|
|
|
|
1 |
2 |
3 |
4 |
|
Рис. 1. Многоугольник распределения
22
|
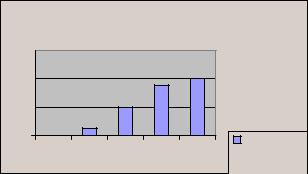
функция распределения F( х) : |
|
||||
1,5 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0,5 |
|
|
|
|
|
|
0 |
|
|
|
|
функция |
|
1 |
2 |
3 |
4 |
5 |
||
распредел |
||||||
|
|
|
|
|
ения F( х) |
|
Рис. 2. Функция распределения
2.2.Числовые характеристики дискретных случайных величин
1)Математическое ожидание М(Х) дискретной случайной величины Х это сумма произведений всех возможных значений величины Х на соответствующие вероятности:
М(Х) = x1· p1 + x2· p2 + … + xn· pn. |
(1.4) |
Свойства математического ожидания:
1.Математическое ожидание имеет ту же размерность, что и сама случайная величина.
2.Математическое ожидание может быть как положительным, так и отрицательным числом.
3.Математическое ожидание постоянной величины С равно этой постоянной. М (С) = С.
4.Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин.
М(X + Y + . . . + W) = М (X) + М (Y) + . . . + М (W).
5.Математическое ожидание произведения двух или нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин.
М(XY) = M(X) M(Y).
6.Постоянный множитель можно выносить за знак математического ожидания:
М(СХ) = С М(Х).
2) Дисперсия D(X) дискретной случайной величины Х – это математическое ожидание квадрата отклонения случайной величины Х от ее математического ожидания:
D(X) = M [X – M(X)]2. |
(1.5) |
Формула (1.5) после возведения в степень и преобразований имеет вид:
D(X) = M (X2) – [M(X)]2. |
(1.6) |
Свойства дисперсии:
Дисперсия имеет размерность, равную квадрату размерности случайной величины. Дисперсия постоянной величины всегда равна нулю: D (С) = 0.
Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D (СX) = С2 D(X).
Дисперсия алгебраической суммы двух независимых случайных величин равна сумме их дисперсией: D(X +Y) = D(X) + D(Y).
3) Среднее квадратическое отклонение σ(Х) дискретной случайной величины Х определяется формулой (1.2). Среднее квадратическое отклонение имеет ту же размерность, что и случайная величина.
23