
геометрия метод указания
.pdf
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЯ Тольяттинский государственный университет
Кафедра "Начертательная геометрия и черчения"
Методические указания
по решению задач в рабочей тетради.
Тольятти 2006

ÓÄÊ 514. 18 (076)
Методические указания по решению задач в рабочей тетради /Сост. Яковлева Т.М. Варенцова Т.А., Уполовникова Г.Н. - Тольятти, ТГУ, 2006 - С
Является завершающей составной частью учебного пособия по курсу "Начертательная геометрия"
Содержит подробное объяснение (текстовую и графическую "инструкцию") решения графических задач из "Рабочей тетради".
Для студентов технических специальностей высших учебных заведений.
Утверждено НМС Тольяттинского государственного университета
Научный редактор: к.т.н., доцент Виткалов В.Г.
С Тольяттинский государственный университет, 2006

Содержание (методические указания по решению задач) Р-3
¹ задачи..........Страница
Модуль ¹1
1. Точка........................................................................................................................................ |
1, 2................................ |
2 |
2. Линия...................................................................................................................................... |
3, 4,10, 11, 13........... |
4 |
Модуль¹2 |
|
|
1. Плоскость......................................................................................................................... |
17, 18. 20, 23.......... |
8 |
|
25, 27, 30, 31 |
|
2. Поверхность................................................................................................................... |
32, 33. 34, 35........ |
16 |
|
38, 42, 43, 46, |
|
Модуль ¹3 |
47, 50 |
|
|
|
|
Главные позиционные задачи |
|
|
1. Решение задач по 1 и 2 алгоритмам............................................................... |
55, 58, 60, 61...... |
23 |
|
64, 67, 76, 78 |
|
2. Решение задач по 3 алгоритму........................................................................... |
71, 73...................... |
29 |
Модуль ¹ 4 |
|
|
1. Метрические задачи....................................................................................................... |
86, 89, 91.............. |
52 |
|
92, 95 |
|
2. Метод введения новой плоскости проекций............................................... |
100, 102, 104......... |
55 |
|
105, 106, 107, 109 |
|
3. Метод вращения вокруг проецирующей оси............................................... |
115, 116...................... |
..66 |
Ð-3
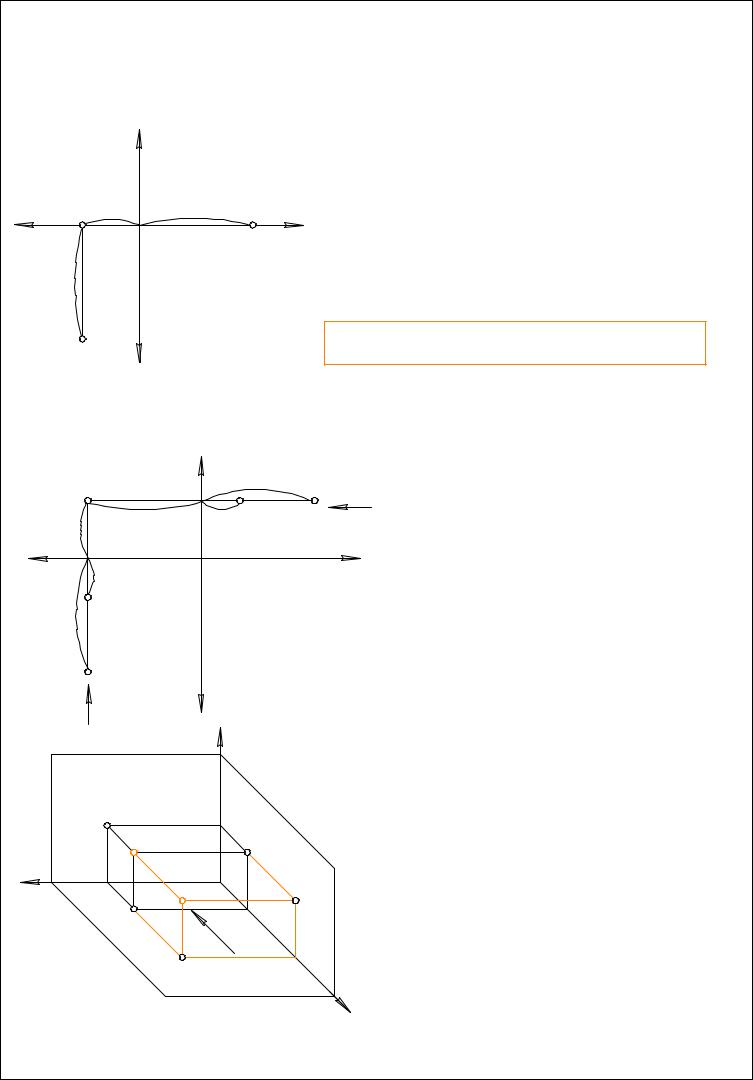
Решение задачи 1. |
|
Построить комплексные чертежи точек: А(15,30,0), |
Â(30,25,15), |
||||||||||||
|
|
|
|
|
|
Ñ(30,10,15), |
D(15,30,20) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Решение задачи разделим на четыре этапа. |
||||||||
|
|
|
|
|
|
|
|
1.1 À(15,30,0) |
XA = 15 ìì |
||||||
|
|
|
z |
|
|
|
|
|
|
|
|
yA = 30ìì |
|||
|
|
|
|
|
|
|
|
|
|
|
zA = 0. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Êàê |
Вы думаете, если у точки А координата ZÀ=0, |
|||||||
x |
A |
|
|
|
|
A3 |
то какое положение она занимает в пространстве? |
||||||||
|
15 |
30 |
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
Если у точки одна координата равна "0", то точка |
|||||||||
|
|
|
|
|
|
y |
|||||||||
|
|
|
|
|
|
принадлежит одной из плоскостей проекции. В данном |
|||||||||
|
|
|
|
|
|
|
|||||||||
|
0 |
|
|
|
|
|
случае у точки нет высоты: z = 0, следовательно т.А |
||||||||
|
3 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
лежит в плоскости П1 . |
|
|
|
|
||||
|
A1 |
|
|
|
Ðèñ. 1.1 |
|
На комплексном чертеже оригинал (т.е. сама |
||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
точка А) не изображается, есть только ее проекции. |
||||||||||
|
|
|
|
|
|
||||||||||
Так выглядит комплексный |
чертеж т.А, |
|
1.2 |
Â(30,25,15) è |
Ñ(30,10,15) |
||||||||||
построенный по заданным координатам. |
|
На втором этапе объединим построение двух точек. |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
z |
|
|
|
|
xB = 30ìì |
|
xC = 30ìì |
|||
|
|
|
|
|
|
|
|
|
yB |
= 35ìì |
|
yC |
= 10ìì |
||
|
B2 =(C2 ) |
|
|
25 |
Видимость |
|
|
||||||||
|
|
|
|
zB |
= 15ìì |
|
zC |
= 15ìì |
|||||||
|
|
|
|
относительно П |
|
||||||||||
|
|
|
|
|
|
C3 |
|
|
2 |
|
|||||
|
|
|
|
|
|
B |
|
|
|
||||||
|
|
|
30 |
|
10 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
3 |
|
У точек "В" и "С": |
xB = xC |
|
= 30ìì |
||||
x |
|
|
|
|
|
|
y |
|
|||||||
|
|
|
|
|
|
|
|
|
zB |
= zC = 15ìì |
|||||
|
|
|
10 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
C1 |
|
|
|
а) Координаты |
õ |
точек одинаковы, следовательно, в |
||||||
|
|
|
|
|
|
системе П1 -Ï2 |
проекции точек лежат на одной |
||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
линии связи (рис. 1.2), |
|
|
|
|
||||
|
|
|
B1 |
|
y |
Ðèñ. 1.2 |
б) Координаты z точек совпадают, (обе точки |
||||||||
|
|
|
Видимость |
|
|
одинаково удалены от П1 íà 15ìì,) |
|
т.е. они расположены |
|||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
относительно П2 |
|
|
|
на одной высоте, следовательно на П2 проекции точек |
||||||||
|
|
|
|
|
|
z |
|||||||||
|
|
|
|
|
|
совпадают: В2 |
= (Ñ2 ). |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
в) Для определения видимости относительно П2 смотрим |
||||||||
|
B2 =(C2 ) |
|
|
|
на рис. 1.3. Наблюдатель видит т.В, которая закрывает |
||||||||||
|
|
|
Ñ |
|
|
C3 |
собой |
т.С, т.е. т.В расположена ближе к наблюдателю, |
|||||||
|
x |
|
|
|
|
|
поэтому на П2 |
она видима. (См |
Ì1 - 13 è 16). |
||||||
|
|
|
|
 |
|
B3 |
В системе П2 Ï3 проекции точек также |
||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
C1 |
|
|
|
|
лежат на одной линии связи и видимость |
|||||||
|
|
|
B1 |
|
Видимость |
|
определяется по стрелке (рис. 1.2). |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Ðèñ. 1.3 |
|
относительно П2 |
y |
|
|
|
|
|
|
|
|
||
|
|
|
Точки В и С - называются фронтально конкурирующими. |
||||||||||||
|
|
|
|
|
|
|
Ð-4 |
|
|
|
|
|
|
|
|
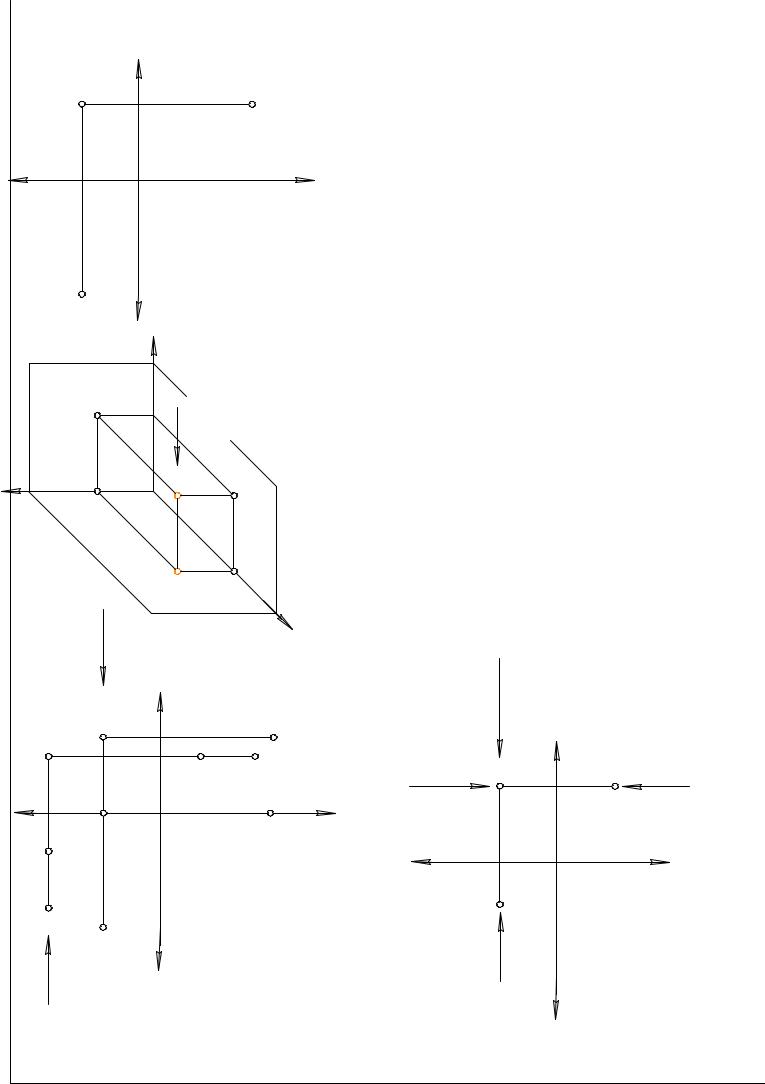
|
Z |
|
1.3 |
D (15,30,20) |
XD = 15ìì |
|
||
D2 |
|
|
|
|||||
XD=15 |
YD=30 |
|
|
|||||
|
YD = 30ìì |
|
||||||
|
|
|
||||||
ZD=20 |
|
|
D3 |
|
ZD = 20ìì |
|
||
|
|
|
|
|
||||
|
|
Y |
а) На этом комплексном чертеже (рис. 1.4) построены |
|||||
X |
|
|
||||||
|
|
|
|
три проекции ò.D.(D1 ,D2 ,D3 ). |
|
|||
YD=30 |
|
|
Все три координаты |
имеют числовые значения, отличные |
||||
|
|
от нуля, поэтому точка не принадлежит ни одной |
||||||
|
|
|
|
|||||
|
|
|
|
плоскости проекций. |
|
|
||
D1 |
Y |
|
Ðèñ. 1.4 |
б) Совместим пространственное изображение А и D |
||||
|
|
(рис. 1.5). В системе П1 -Ï2 |
проекции точек А и D лежат |
|||||
|
|
|
|
|||||
|
z |
|
|
на одной линии связи, только т.D выше т.А, следовательно |
||||
|
|
|
D1 - видима, а А1 - невидима (видима на П1 та точка, |
|||||
|
|
|
|
которая располжена выше) |
|
|
||
|
D2 |
Видимость |
|
|
|
|
||
|
|
относительно П1 |
|
|
|
|
||
x |
A2 |
D |
D3 |
Точки А и D - называются |
||||
горизонтально конкурирующими. |
||||||||
|
|
|||||||
|
|
|
A3 |
|
|
|
|
|
|
(À=A1 |
)=D1 |
y |
Ðèñ. 1.5 |
|
|
|
|
|
|
|
|
|
|
|||
|
Видимость |
|
|
|
|
Направление взгляда |
||
|
относительно П1 |
|
|
|
для определения |
|
||
|
|
Z |
|
|
|
видимость |
|
|
|
|
|
|
|
относительно П1 |
|
||
|
D2 |
|
D3 |
Направление взгляда |
|
Направление взгляда |
||
Â2 =(Ñ2 ) |
|
|
|
для определения |
|
Z |
для определения |
|
|
|
|
видимость |
|
||||
|
|
 |
|
видимость |
||||
|
|
Ñ3 |
относительно П3 |
|
|
|||
|
|
|
|
относительно П |
||||
|
|
3 |
Y |
|
|
2 |
||
X |
À2 |
|
À3 |
|
Ì |
Ì |
||
|
|
|
|
|
|
2 |
3 |
|
Ñ1 |
|
|
|
X |
|
|
Y |
|
Â1 |
|
|
|
Направление взгляда |
Ì1 |
|
||
|
|
|
|
|
||||
|
D1 =(À1 ) |
|
|
для определения |
|
|
||
|
Y |
|
видимость |
|
|
|
||
Видимость |
|
относительно П2 |
|
|
||||
|
|
|
|
|
|
|||
относительно П2 |
|
|
|
|
|
|
||
Рис. 1.6. На четвертом, завершающем этапе, |
|
Y |
|
|||||
|
Ðèñ. 1.7 |
|
||||||
соединим все три фрагмента комплексных |
|
|
||||||
чертежей точек À,Â,Ñ,Ä |
в один общий. |
Ð-5 |
|
|
|
|||
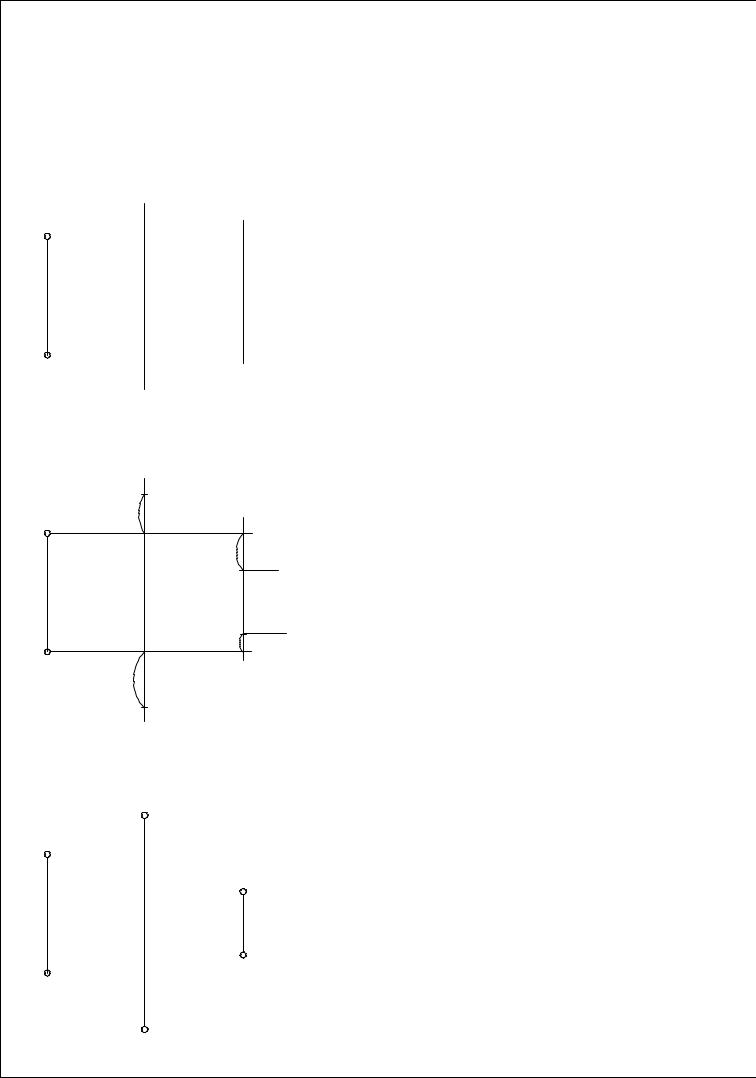
Решение задачи 2.
На заданных линиях связи построить проекции точек Â è Ñ: точка Â расположена выше точки А на 10мм и ближе к наблюдателю на 15мм; точка Ñ расположена ниже точки À на 10мм и ближе к плоскости П2 íà 5ìì.
À2
À1
À2
À1
À2
À1
Линия связи т.В
Â2
ì ì 0 1
15ìì
Â1
Â2
Линия связи т.С
ì ì 0 1
5ìì
Ñ2
Ñ1
Ñ2
Ñ1
Решение задачи осуществляется на безосном комплексном чертеже.
1. Распределим линии связи для т.В и т.С
2. Проведем вспомогательные линии А1 À2 , пересекая линии связи точек В и С.
Верхняя горизонтальная линии от А2 будет определять уровень точек В и С относительно П1 , по сравнению с т.А, т.е. "выше - ниже" т А:
т.В выше на 10мм; чем т.А относительно П1 т.С ниже на 10мм, чем т.А относительно П1
3. Нижняя горизонтальная линия от А1 будет границей расположения точек В и С относительно П2 , по сравнению
ñт.А, т.е. "ближе - дальше" от наблюдателя: т.В ближе на 15мм к наблюдателю, чем т.А, т.С дальше от наблюдателя, т.е. ближе к П2
íà 5ìì, ÷åì ò.À.
4.Убираем все вспомогательные построения.
Задача решена..
Â1 Ð-6
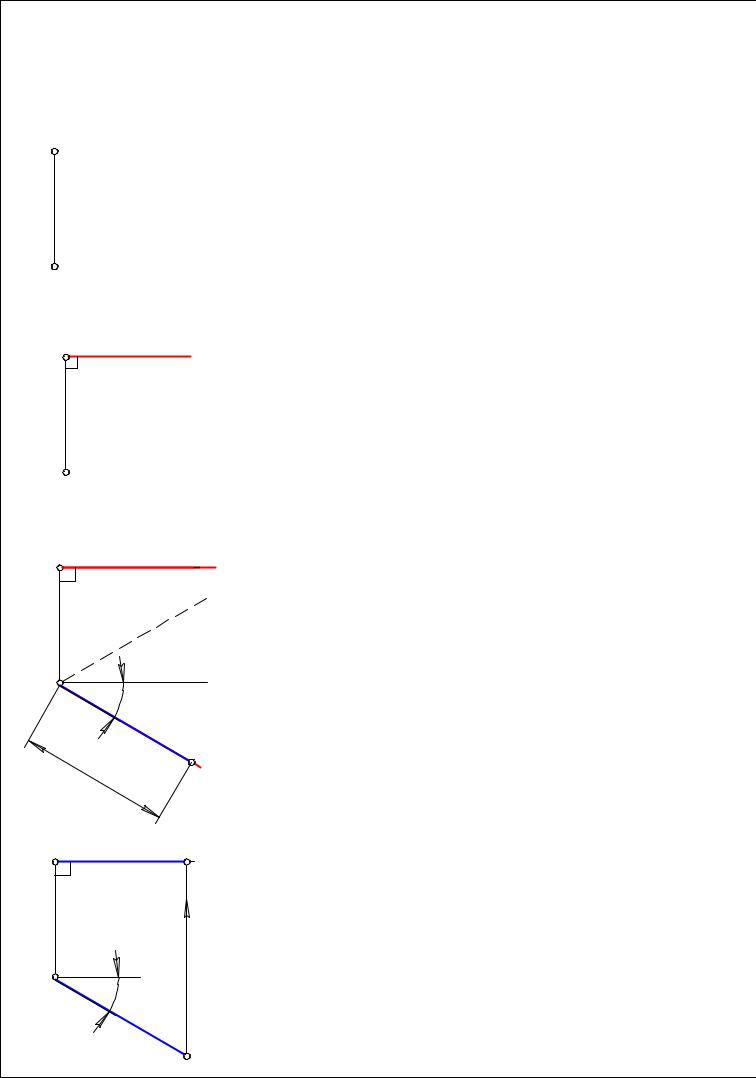
Решение задачи 3.
Решение задачи 4.
À2
À1
Для решения этой задачи, при необходимости, можно воспользоваться Модулем ¹1, стр. 20-23.
Построить проекции отрезка АВ горизонтали h(h1 h2 ) 2 Ï1 åñëè β=30°, |ÀÂ |= 40мм, точка В удалена от П2 дальше, чем т.А.
Решить эту задачу, значит построить т.В (В1 Â2 ). h2 линии связи,
h1 - проецируется в истинную величину,;
β - угол наклона горизонтали к П2 проецируется без искажения.
Алгоритм построения.
h2
À2
À1
À2
À1
40
1. Горизонталь начинаем строить с фронтальной плоскости: h2 лин. связи. Можно ли отложить на этой линии 40мм и построить т.В2 ?
Нельзя, т.к. h2 проецируется с искажением.
h2
|
|
|
|
|
|
|
|
|
|
|
2. Íà Ï 1 проведем вспомогательную прямую из |
ò.À1 À1 À2 . |
|||
|
|
|
|
|
|
|
|
|
|
|
3. Построим угол β. Его можно отложить вверх |
îò |
|||
|
|
|
|
|
|
|
|
|
|
|
вспомогательной линии и вниз, но в задаче дано, что т.В |
||||
° |
|
|
|
|
|
|
|
|
|
удалена от П2 дальше, чем т.А, |
поэтому луч для β = 30° |
||||
|
|
|
|
|
|
|
|
|
откладываем вниз. |
|
|
|
|
||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
h |
|
|
|
|
|
|
|
|
4. На этом луче откладываем расстояние, равное |
|
|||
|
|
|
è |
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
ñ |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
ò |
|
|
|
|
|
|
= |ÀÂ | |
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
í |
|
|
|
h |
= À Â |
|
|
|
|
â |
|
֏ |
í |
|
40мм и получаем: |
|
|||||||
|
|
|
|
à |
|
||||||||||
|
|
|
å |
|
|
|
|
|
ÿ |
Â1 |
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
è |
íà |
|
|
1 |
1 1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
À2
À1
h2
° |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
β |
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
è |
|
|
|
|
|
|
|
|
ñ |
|
|
|
|
|
|
|
ò |
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
í |
|
|
|
|
â |
|
í |
|
||
|
|
|
|
à |
|||
|
|
|
å |
|
|
ÿ |
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
í |
|
|
|
|
|
|
|
à |
|
|
Â2
5. Так как мы построили горизонтальную проекцию т.В → Â1 ,
то для определения |
Â2 достаточно провести линию связи |
до пересечения с h2 |
→ Â2 . |
Â1 Ð-7
Решение задачи 6. |
Построить проекции отрезка |МN| =30мм горизонтально |
проецирующей прямой при условии, что точка В делит отрезок пополам. |
|
1. Горизонтально проецирующая прямая |
MN параллельна сразу двум плоскостям проекций: П1 . Ï2 (Ì1 - 22) |
2. Фронтальная ее проекция -M2 N2 проецируется без искажения на П2 и совпадает с с линиями связи, а горизонтальная проекция проецируется в точку, которая называется главной проекцией и обладает собирательными свойствами (М1 =N1 =Â1 ).
15 |
|
Ì2 |
|
B2 |
|
B2 |
B2 |
|
15 |
|
N2 |
|
|
|
B |
B |
(B1 =N1 )=Ì1 |
1 |
1 |
|
Отложить 15мм вверх |
Â1 =N1 =Ì1 -горизонтально |
|
è âíèç îò |
ò.Â2 |
конкурирующие точки |
Решение задачи 8.
À
DZ
À
À1
DZ
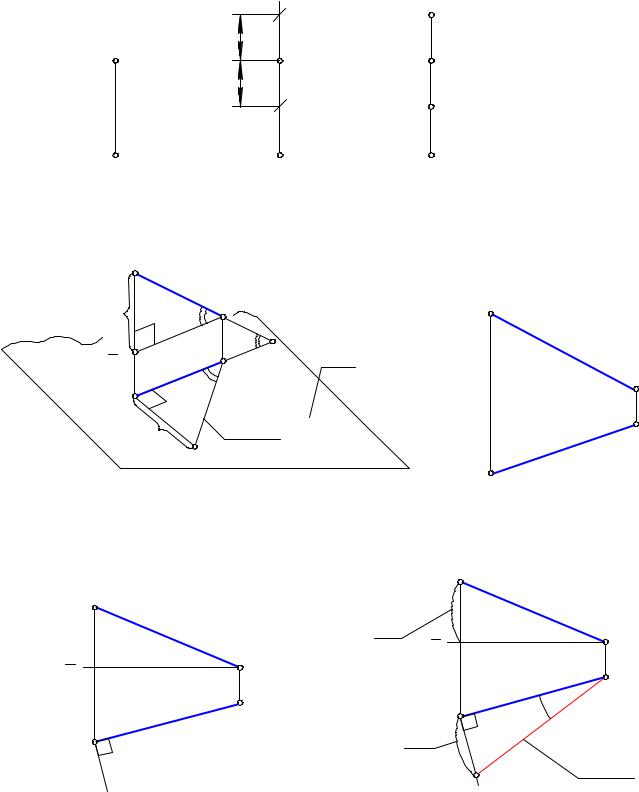
Определить истинную длину отрезка АВ и углы его наклона к плоскостям проекций П1 è Ï2
a |
|
|
 |
À2 |
// |
|
|
a |
Ï1 |
// |
|
|
Â1 |
|
a |
|
Â2 |
||
|
S |
Натуральная |
||
|
|
|
||
|
|
величина |
|
|
|
|
|
Â1 |
|
|
|
|
отрезка АВ |
À1
1.Анализ условия: ни одна из проекций отрезка АВ не ||и не линиям связи, значит задана прямая общего положения (Модуль ¹1, стр. 20).
2.Двухкартинный чертеж Монжа обратим, поэтому для нахождения натуральной величины отрезка АВ применяют метод прямоугольного треугольника. (Модуль ¹1, стр. 14).
|
|
|
|
|
À2 |
|
|
|
À2 |
|
|
Z |
|
|
|
|
|
|
Â2 |
|
|
|
|
|
|
À |
|
|
|
À |
Â2 |
|
|
Â1 |
|
|
|
|
|
||
|
|
À1 |
Â1 |
|
À1 |
a |
|
|
|
|
Z |
Натуральная |
|
|
|
|
|
|
|
величина |
|
|
|
|
|
À0 |
отрезка АВ |
|
|
|
|
|
|
|
À |
В - первый катет. Перпендикуляр к А В |
À1 À0 -второй катет. Гипотенуза А0 Â1 -это натуральная |
||||
1 |
1 |
|
1 |
1 |
величина |ÀÂ|. Óãîë α -есть угол наклона АВ к П1 . |
|
можно провести как из т.А1 , òàê è èç Â1 . |
|
|||||
Аналогично, можно найти натуральную величину отрезка АВ и угол (β) наклона данного отрезка АВ к П2 , построив прямоугольный треугольник на П2 . Самостоятельно.
Ð-8

Решение задачи 10.
À2
À1
Построить горизонтальную проекцию отрезка АВ, еслиβ = 20°(угол наклона к П2 ), т.В дальше от П2 , ÷åì ò À.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
ò |
ü |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
î |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
ð |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
ò |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
ñ |
|
|
|
|
|
|
è |
|
||
|
|
|
|
|
|
|
î |
|
|
|
|
|
|
ê |
|
|||
|
|
|
|
° |
|
ï |
|
|
|
|
|
|
ñ |
Решение задачи сводится к построению |
||||
|
|
|
|
|
|
|
|
|
|
|
å |
|
||||||
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|||||
|
β |
= |
2 |
0 |
|
|
|
|
ô |
è |
|
|
|
|
|
|
горизонтальной проекции т.В → Â1 , ò.å. |
|
|
|
|
|
|
à |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
ð |
|
|
|
|
|
|
|
|
|||||
|
|
|
ã |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
надо определить разность удаления |
||
Â2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
Å |
концов отрезка АВ до П2 . |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||
Как это можно сделать?
Только построив прямоугольный треугольник на П2 (задача 8). Достаточно ли в условии для этого информации? Да, т.к. есть один катет А2 Â2 и угол наклона гипотенузы к нему.
À2 |
À2 |
|
|
|
Â2 |
|
|
|
Â2 |
À1 |
|
|
* |
À1 |
|
|
* |
|
 |
 |
|||||
|
|
|
|
|
|||
Провести линию связи из В , т.к. В -В |
находятся на одной |
À2 Â2 - первый катет. |
|||||
2 |
1 |
2 |
|
|
Перпендикуляр (второй катет) можно |
||
линии связи. Провести из т.А вспомогательную прямую |
|
||||||
À1 À2 , т.к. по условию т.В дальше от П2 , ÷åì ò.À. |
|
проводить из любой точки А2 èëè Â2 . |
|||||
À2
R
À1
À2
À1
l |
|
ó |
R |
|
|
||
|
|
|
|
|
Â2 |
Построить из т.А2 óãîë 20° |
l |
 |
* |
(перенести графически) |
2 |
|
с помощью циркуля. |
||
|
0Å |
 Â0
Â0
|
|
ó |
Â2 Â0 ( у) - второй катет |
|
 |
|
|
|
|
Гипотенуза А2 Â0 -натуральная величина |
|
|
2 |
|
отрезка АВ. |
|
* |
|
|
 |
|
Â2 Â0 -значение второго катета |
|
ó |
|
отложить от точки В →Â1 . |
|
|
|
Â1 Ð-9

|
Решение задачи 11.3. Через т. А провести прямую m _ n, если Е m, C n, т.Е |
||||||||||||
|
Ñ2 =Å2 |
|
À2 |
|
расположена перед С на 10мм. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
m2 |
|
n2 |
|
Прямые m и n скрещивающиеся, значит у них нет общих точек. Точки |
|||||||||
|
|
|
Е и С - фронтально конкуририрующие, т.е. точки С и Е лежат на |
||||||||||
|
|
|
n1 |
|
одном к П2 , поэтому С1 |
è Å1 |
лежат на одной линии связи. |
||||||
|
Ñ1 |
|
|
|
|
|
|
(Ñ2 )=Å2 |
|
À2 |
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
À1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
À |
|
|
m2 |
|
|
|
|
|
|
|
|
Ñ2 =Å2 |
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
n |
|
|
|
m2 |
|
|
|
|
|
m1 |
|
Ñ1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
10ìì |
|
|
|
|
|
m1 |
Ñ1 |
|
n1 |
|
|
D1 =F1 Å1 |
|
À1 |
|
|||
|
10ìì |
|
|
|
|
|
Видимость |
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
Å1 |
|
|
|
|
|
относительно П2 |
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
À1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Через две точки А1 |
è Å1 , проводим |
|
m1 , ò.Å(Å1 ) расположена |
|||||
|
Продлите линию связи из т.С1 . |
|
ближе к наблюдателю, значит на П |
|
фронтальная проекция |
||||||||
|
От точки С1 отложите 10 мм |
|
ò.Ñ(Ñ2 )- невидима, взять в скобки.. |
2 |
|
|
|||||||
|
|
|
|
|
|
||||||||
ближе к наблюдателю →получим ò.Å1 . |
|
|
|
|
|
|
|
|
|||||
|
Точки D и F- горизонтально конкурирующие, построить их фронтальные проекции и |
||||||||||||
|
определить видимость самостоятельно (Модуль ¹1, стр.26). |
|
|
|
|
||||||||
|
Решение задачи 13. |
Построить горизонтальную проекцию плоской кривой m. |
|||||||||||
|
1 |
Â2 |
|
|
m2 |
11 = ?, |
21 = ?, m1 = ?. |
|
|
|
|
||
|
22 |
|
|
|
|
|
|
|
|
|
|||
À2 |
2 |
|
|
|
Для построения проекций плоской кривой применяется |
||||||||
|
|
|
Ñ2 |
||||||||||
|
|
|
|
|
метод хорд. Кривая считается плоской, если проекции |
||||||||
|
Â1 |
|
|
|
|
точки пересечения проекций одноименных хорд лежат на |
|||||||
À1 |
|
|
|
|
одной линии связи (Модуль ¹1, стр. 29). |
|
|||||||
12 |
Â2 |
|
|
Ñ1 |
|
|
12 |
 |
|
|
|
|
|
|
|
22 |
|
|
|
2 |
22 |
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
m2 |
|
|
|
|
m2 |
||||
À |
32 |
|
|
|
À2 |
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
||
2 |
|
|
|
Ñ2 |
|
|
|
|
|
|
|
Ñ2 |
|
|
|
Â1 |
|
|
|
|
|
Â1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Ñ1 |
||
|
|
|
|
|
Ñ |
À |
|
3 |
|
|
|
||
À1 |
|
|
|
|
1 |
|
1 |
|
|
|
|
||
|
|
|
1 |
|
Опустив линию связи из т.32 , находим т.31 |
||||||||
|
|
|
|
|
|
||||||||
Строим хорду АВ на П1 è Ï2 . Íà Ï2 |
|
||||||||||||
|
Точка |
3(32 ,31 ) позволит построить |
|||||||||||
строим фронтальную проекцию хорды 12 Ñ2 . |
горизонтальную проекцию хорды 1С. |
||||||||||||
|
À2 Â2 ∩ 12 Ñ2 = 32 |
|
|
Ð-10 |
|
|
|
|
|
|
|
||
