Разбор лекций

Все требования кгруппе выполнены,азначит Н – этоподгруппа G.

Следствие 1.

ПодмножествоН группы Gявляется подгруппой Gтогда и толькотогда,когдаa*b-1 H.

Бездоказательства

Следствие 2.

Если группаGконечна,тоее подмножествоН является подгруппой G,если для любыхa,b H

выполняется a*b H.

Доказательство.

Издоказательствапредыдущей теоремы мы поняли,чтодля того,чтобы доказать,чтоHгруппа (подгруппа),достаточнопроверить замкнутость и наличие обратногоэлемента– остальное и такбудет выполняться. Проверимих.

Пусть порядокord(a)=n,тоесть an=e. Разделив наa,получаемa-1=an-1.

Замкнутость же следует изусловия следствия.

Утверждение Лагранжа.Порядокгруппы делится на порядоклюбой ее подгруппы.

Бездоказательства.

Другими словами:если дана подгруппа какой-тогруппы,топорядокисходной группы обязательноделится на порядокзаданной ее подгруппы. Ведь подгруппа – это«кусочек» исходной группы.

Напомним,чтопорядокэлементаg – этотакой наименьший натуральный t,чтоgt=e.

Тоесть g-1=gt-1 (получается,если разделить обе частиgt=e наg-1).

Порядокэлементаg обозначается ord(g)=t

Экспонента группы G– этонаименьшее натуральноеt,такое чтоgt=e для любогоэлемента из G(не толькозаданногоg). Обозначается exp(G) = НОК(ord(g1)…)

Свойстваэлементовg.

Пусть g G имеет конечный порядокt(gt=e). Тогда:

Свойство1.

t|exp(G) и exp(G) ||G| -экспонентаделится наtи порядокгруппы делится наэкспоненту. Доказательство. Еслиt конечно,тоg порождает подгруппу группы G. Мощность <g> равна ord(g) – порядку элементаg (минимальной степениt,в которойgt=e). Мощность действительноравна порядку,т.к. поусловиюg имеет конечный порядокt,а значит является циклической,азначит ее мощность – количествоэлементов вцикле:это количествои показываетord(g).

Итак,получили подгруппу <g> мощности t=ord(g). Потеореме Лагранжа(чуть раньше она была) порядокгруппы делится напорядоклюбой ее подгруппы. Отсюда|<g>|||G|-то есть |G|делится на|<g>|. Номы получили,что|<g>|=ord(g).

Поэтому ord(g) ||G|-Gделится наord(g). Так как элемент g выбирался случайно,тоэто справедливодля любогоg,а значит,Gделится напорядоккаждогоэлементав группе. Это означает,чтоНОК(ord(g1)…) ||G|или (поопределениюэкспоненты) exp(g) ||G|.

Тот же факт,чтоэкспонентаделится наt=ord(g),где g выбран произвольно,следует непосредственноизопределения экспоненты:онаявляется НОК для порядков всех элементов,а значит,делится на каждый изних. Напомним,порядок– этоord(g).

Свойство2.

gn=e  nделится наt,где t– минимальный,такой чтоgt=e. Тогдаgn=e  n=t*p,где р– произвольное число.

Другими словами:все логично– если gt=e,тоgt*p=e. Здесь сказаноименноэто,просто более научнымязыком.

Свойство3.

Элементы gi и gt-i являются взаимно-обратными,если ord(g)=t(т.е. gt=e,t-минимальное) Другими словами:ничегонового,простообозначение.

Свойство4.

Порядокэлементаgi равен: Ord(gi) = НОД( , ),где i=1...t.

Другими словами:известен ord(g)=t,есть gi,и намнужнонайти такой минимальный М,что giM=e. Уже понятно,чтоiMбудет равноили кратноt. А если по-научному,то:посвойству 2 получаем:t|iM– тоесть iMделится наt.

Пример.

Покажем,чтоформула работает. Пусть заданоt=2*32*53*74*11и i=2*32*19*23. Нужноi на что-тоумножить,чтобы получить то,чтоделится наt. Начтоименно?На вот этот «хвост»:53*74*11). Смотрите,каклегкоэтот хвост получается понашей формуле:

Ответ:ord(g2*3^2*19*23) = 53*74*11

Свойство5. Любая группа простогопорядкаявляется циклической,т.е. порождается одним элементом(поопределению– группа называется циклической,если порождается одним элементом).

Для начала вспомнимпервое свойство– аименното,что|G|делится на exp(G)=НОК(ord(g1)…).

Если порядокG – простое число,то expтоже должна быть равна или 1(если элементg, порождающий группу,равен единице),или этому простому числу вовсех остальных случаях (т.к. |G|делится наexp,ачисло|G|- простое,и ни на чтобольше делиться не может).

А если экспонента (равная НОК!) равна простому числу|G|, тоord(g)=|G|=> |G|=|<g>|. Переход |<g>|=ord(g) рассматривали совсемнедавно,чуть выше.

Далее мы продолжимразговороб элементах и их порядках,атакже встретимкое-что совсемновое– научимся обозначать перестановкибуквами и выполнять разныедействия сними. Давайте продолжим:)

Этатеоремаи ее доказательствоне сложныеи понятные,нодоказательствоу нее «пестрое»,немногофрагментированное – разбросанное поуглам. Какне старался его систематизировать – полностьюэтосделать не получилось,оноот природы такое. Поэтому изучать егонужновнимательно. Закройтевкладку скотятами,выключите радио, глубоковдохните и приготовьтесь наодномдыхании разобраться сдоказательством. Потому чтоесли отвлечетесь,придется начинать все заново.

Теорема. Если элементы g и hизгруппы Gперестановочны (gh=hg),причемпорядок элементаg равен h(т.е. ord(g)=n),а порядокэлементаhравен m (т.е. ord(h)=m),товG найдется элемент порядкаНОК(m,n).

Доказательство. Рассмотрим2случая для чиселm и n:они могут или быть взаимно простыми,или нет. Начнемспервого.

Пусть nи m – взаимнопростые,тогда НОД(m,n)=1.Таккак они перестановочны,то обозначимt=НОК(m,n),и тогдабудет справедливоследующее:

(gh)t=gtht=e.

Поясним,откуда взялось равенствоединичному элементу. Поусловиюord(g)=nи ord(h)=m. Вспомним,чтотакое ord(порядокэлемента). Ord(g) = t:gt=eg. Совсемнедавно былопоказано,чтоеслиgt=eg,тои gt*n=eg. В нашемслучаеt=НОК(m,n)=m*n(равноm*n, т.к. числа взаимнопростые). Поэтому gt=e и ht=e. Отсюдаgtht=e*e=e.

С учетом t=НОК(m,n)=m*n,можнозаписать: (gh)t=(gh)m*n=e

Отсюда имеемord(gh) |mn– порядок(gh) делится наmn. Все логично.

Теперь сделаемследующий шаг. Обозначимord(gh)= τ=u*v, где u|nи v|m (nделится наu; m делится наv). Определимминимальновозможное значениеu(для v этоделается аналогично).

Таккак g и hперестановочны,можнозаписать: (gh)tay = (gh)u*v = e

gu*v hu*v=e

Заметим, чтоuv|um (так как мы взяли такойv, что m делится наv).

Учитывая,что (gh)u*v =e(даетсаморавенство),а такжеuv|u (даеттот факт, чтовстепени um это тоже будетравно единичномуэлементу), можно записать:

(gh)um=e–и правда, мыжетолько для uминимум ищем

Так как g и hперестановочны, тоэтоможнопереписать ввиде: gum hum =e

Вспомним,что поусловию унасm –порядок элементаh, поэтомуhum=e.

Получили:gum е=e Отсюда gum=e

Вспомним,что порядок элементаg равенn. То есть длявыполненияусловияgum=eдолжно выполнятьсяследующее–nдолжен делитьсяна um. Так как nи m –поусловиювзаимно простые, то в данном случае минимальноевозможноезначениеuравно n.

Аналогично можнополучить,что минимальноезначение v=m апоэтомуord(gh)=m*n.

Давайтеещераз посмотрим, чтожетут произошло. Мыпоказали, что(gh)m*n=e. Так какэто равно единичномуэлементу, тоord(gh) делится наm*n. Теперь обозначим ord(gh)= τ=u*v (причем u|nи v|m ) и попробуемнайти минимально-возможные uи v. Заметим, чтоum делится наuv, так что ничего неизменится,если uvзаменить на um – равенство (gh)u*m=eостанетсяверным. Нотогда hum=e, азначити gum=e. Нодля выполненияэтогоусловия необходимо, чтобыстепень(um)

делилась наn, т.к. n–порядокэлементаg. Так как элементы nи m – взаимнопростые, ихНОК равенm*n. Азначит, минимальновозможноеu=n. Рассуждая аналогично, можнополучить,что минимально возможное v=m (сведяк случаю hun=e).

Получили:ord(gh)= τ=u*v = НОК(m,n) =n*m.

Ну вот, дляслучая, когдаm и n –взаимно простые,доказали.

Рассмотрим случай, когдаm и n –невзаимно простые.

ОбозначимНОД(m,n)=d. Тогдапорядок ord(gd)= . Почему? Ну вотсмотрите: g20 =e, отсюда ord(g)=20

(g4)5=e, тогда ord(g4)=20/4=5

Заметим, чтоНОД( , m) = 1(потомучто dпоусловию–наибольший общий делитель,и если одно из чисел разделить на него, тоони станут взаимнопростыми).

Получили: Ord(gd) =

Ord(h)=m

Причемn/dи m –взаимно простые. Ничегоне напоминает? Даэтожепервый пункт, который мы уже доказали! Переднами действительно 2элементаиих порядки взаимнопростые. Тогда, как мы уже доказали,ord(gdh) будет равен произведениюэтихпорядков.

Ord(gdh) = =НОД( , ) = НОК (m,n).

Здесь мыпоказали,что если порядки уg и h невзаимно-простые, топри выбореопределенногоd будут простыми порядки уgd и h. Степень у«g» здесь непринципиальна –нам же неважно, какие именно этоэлементы, мыхотели доказать,что найдетсяэлемент порядка НОК(n,m). Ион нашелся– (gdh).Егодоказательство сводитсяк первомупункту –когдаm и nвзаимно простые.

Эта теоремапоказывает нам, чтоесли есть 2перестановочныхэлемента порядков m и n–всегда найдетсяэлементпорядка НОК(m*n). Независимо оттого, являютсялиm и n взаимнопростыми. Теорема доказана.

Следствие. Если G –абелевагруппа(группа,гдевыполняется коммутативность (x*y = y*x)),товG

найдется элемент g,такой чтоord(g) = exp(G) = НОК(ord(k)),где k принадлежит G. Заметьте,здесь условие распространяется не на конкретныеg и h,какв предыдущей теореме,аналюбые два элемента(g и k,где k – любой изG).

Теорема. Всякая подгруппациклической группы также является циклической. Доказательство. Пусть имеется циклическая группа– поопределениюэтогруппа, порожденная 1элементом. Ее граф Кэли– это1 циклбезподходов кнему.

Требуетсяпоказать,что любаяподгруппациклической группыявляетсяциклической,т.е. тоже порождается1элементом.

Пусть H –некотораяподгруппагруппы <g>, причем онагарантированно несостоитиз одногоединственногоединичногоэлемента. Покажем,что онаявляетсяциклической.

Заметим, чтоесли gn H, тоиg-n H – вгруппеналичиеобратного элементаявляется обязательным условием. Такжезаметим,чтоединичный элемент изгруппыGтакже являетсяединичнымэлементом подгруппыH (безнего онабы неназывалась подгруппой).

Пустьd–наименьшеенатуральноечисло,такоечтоgd H. Пустьтакжеgn H.Так какd– наименьшаявозможнаястепень, прикоторой gпринадлежитН,тоn>d. Таккакn>d,то ничегонемешает представить еговлюбом удобномдлянасвиде. Адлянастаким видом будетn=d*q+r,гдеr– остаток отделениячислаnнаd, азначит 0≤r≤d-1. (Пример: n=9, d=7, тогда9=1*7+2).Покажем, чтоэтот остаток равен 0, тогдалюбойэлементиз Н окажетсяпредставим ввиде(gd)q –тоестьдляgn H любойnможнобудет представить в видеd*q.Отсюдабудетследовать, чтоHпорождаетсяоднимэлементомgd, а, значит, и являетсяциклической –то, чтонамнужно.

Апоказать, что r=0, совсем несложно:

gn =gdq+r =gdq * gr

gn =gdq *gr –разделимнаgd gr =gn (g-d)q

Элемент gn принадлежитH, элемент (g-d)q тоже(т.к.в группеесть обратный элемент). Значит,gr тожепринадлежитгруппеН(замкнутость– обязательноетребованиедля группы). Аэтоужепротиворечит условию:ведьмы считали,чтоd– минимальный элемент,такой что gd принадлежит Н.Здесь жеполучили, чтоgr,гдеr<d, тоже принадлежитН.Противоречие– отсюдаr=0.

Как ужеотмечалось в доказательстве, равенствоr=0позволяет говорить отом, чтоподгруппаН порождается1элементом. А значит, являетсяциклической.

Теорема доказана.

Теорема. В конечной циклическойгруппе<g>порядкаnэлемент gr порождаетподгруппупорядка

НОД( , )

Доказательство. Пусть d=НОД(r,n). Порядокгруппы, порожденной элементом gr, равен наименьшемунатуральному t,такому что(gr)t=e–по определению порядка группы. Из того, чтоord(g)=n, атакже(gr)t=eследует, чтоn|rt–rtделится наn.

Имеем n|rt. Разделим обечасти на НОД(r,n)

НОД( , ) | t -- ОТКУДА??????

Минимальноевозможноеt, удовлетворяющееэтому условию, равно

НОД( , )

Теорема доказана.

Эта теоремапоказывает, чтоесли есть циклическаягруппа изnэлементов, то если взять элемент gr,

то порядокпорожденной подгруппы<gr> нам ужеизвестен, и онравен

НОД( , )

Следствие. Конечнаяциклическаягруппапорядкаn, порожденная элементомg, содержитϕ(n) образующихэлементов.

Причемϕ(n) –функция Эйлера,и онаравна количествучисел, которыеменьшеnи взаимно простыес n.

Действительно, если взять r –взаимно простоек n, причем r<n, то, попредыдущей теореме, он породитгруппупорядкаНОД( , ) =n, тоесть исходную группу.

Опр. Отображениеf:G->G’(G и G’–группы) называетсягомоморфизмом, если для любыхa,b из G

выполняется:f(ab)=f(a)f(b).

Опр.Биективный гомоморфизмгрупп(когда указанное соответствиеоднозначное) называется изоморфизмомгрупп.

Утв. Пусть ϕ: G->G’ –гомоморфизмгруппG иG’. Тогда:

1.Если Н–подгруппаG (обозначаетсяH≤G),то ϕ(H)≤G’

2.Если H’≤G’, тоϕ-1(Н’)≤G (здесь G должен быть изоморфизмом)

Докажем пункт 1(второй доказываетсяаналогично).

Чтобы не добавлять лишний текст, давайтезапомним, что обозначение H≤G означает«Нявляется подгруппой G». Хорошее обозначение, унастоящихкриптоаналитиков ни одноутро без негоне обходится.

Нужно доказать,что еслиH≤G, то ϕ(H)≤G’.

Рассмотримэлементы aи bиз подгруппы H. Для нихвϕ(H) найдутсяпрообразы:

ϕ(a)=α

ϕ(b) =β

Так как Н являетсяподгруппойG, то a*b-1 Н.Действительно,т.к.Н –подгруппа,онагарантирует наличиеобратногоэлемента(b-1 Н)и замкнутость (произведениедвух элементов из Нтакже есть элемент изН: a*b-1 Н).

Требуетсяпоказать, чтоϕ(H) являетсяподгруппойгруппыG’.

Толькочтомы получили: a*b-1 Н. Используемэто:

ϕ(b-1b) = ϕ(b)*ϕ(b-1) =e–по определениюгомоморфизма (Отображениеf:G->G’ (G и G’–группы) называетсягомоморфизмом, если для любых a,bизG выполняется:f(ab)=f(a)f(b))

ϕ(b)* ϕ(b-1) =e– разделим наϕ(b-1)

Получим ϕ(b) = ϕ(b-1)-1,или (ϕ(b))-1=ϕ(b-1).

Вспомним,что ϕ(a)=α, ϕ(b) = β. Применимэто:

α*β-1 =ϕ(a)*(ϕ(b))-1 = ϕ(a)*ϕ(b-1) =(поопределениюгомоморфизма) = ϕ(a*b-1). Чуть раньше мыполучили, что a*b-1 Н.

Атеперь запускаем стойкоехэшированиевспоминаем то, чтобыло настранице61. Атамбыла целая теорема! Знаю,что никтоотлистыватьназад небудет,поэтомускопировал еепрямосюда:

Теорема. ПодмножествоН группы Gявляется подгруппой Gтогда и толькотогда,когда:

1.Еслиa,b H, тоa*b H

2.Еслиa H, то a-1 H.

Напомню, намтребуетсядоказать, чтоϕ(H) являетсяподгруппойгруппыG’.

Смотрим натеорему. Пункт1: Еслиa,b H, тоa*b H Мы этоужепоказали: ϕ(a)*ϕ(b-1) =ϕ(a*b-1)

Смотрим на пункт 2: Еслиa H, то a-1 H.

Мы этотоже показали: (ϕ(b))-1=ϕ(b-1). Подробнее:здесь b Н, поэтому b-1 H. Таккак ϕ

являетсяотображением вгруппуG’, то ϕ(b-1) G’.Азначит, и(ϕ(b))-1 G’– чтонами требовалось.

Итак, ϕ(H) являетсяподгруппойгруппыG’. Теоремадоказана.

Теорема.

1.Циклическая группапорядкаm изоморфна аддитивной группе вычетов Zm(+). Напомним, аддитивная группа – группа,заданная относительнооперации сложения.

2.Бесконечная циклическая группа изоморфнаZ(+).

Пример.

РассмотримаддитивнуюгруппуZ8(+).

Граф Кэли для нее выглядит следующимобразом:

Этагруппапорождается единицей. Также присутствует ноль – этоединичный элемент для сложения,он обязательнодолжен быть в группе.

Теоремаговорит отом, чтолюбая группа,порожденная элементомg,изоморфнааддитивной группе Zn,где n=ord(g) – порядокэлементаg. Тоесть когдарассматриваемциклическуюгруппу, она на самомделе изоморфна некоторой группе вычетов. Напомним,изоморфна– значит, совпадает сточностьюдорасстановки вершин.

Кроме того,совсемнедавнобылоутверждение,чтоZn порождается любымэлементом,взаимнопростымсэлементомn. Вот она,CopyPaste сработална твердуюпятерку:

Следствие. Конечнаяциклическаягруппапорядкаn, порожденная элементомg, содержитϕ(n) образующихэлементов.

Причемϕ(n) –функция Эйлера,и онаравна количествучисел, которыеменьшеnи взаимно простыес n.

Действительно, если взять r –взаимно простоек n, причем r<n, то, попредыдущей теореме, он породитгруппупорядкаНОД( , ) =n, тоесть исходную группу.

Такимобразом, Z8 порождается не толькоединицей,нои 3, 5и 7. Не верите?Смотрите. Изтройки можнополучить любое числоот 0до 7вгруппе вычетов Z8:

(3+3)mod8=6

(6+3)mod8=1

(1+3)mod8=4

(4+3)mod8=7

(7+3)mod8=2

(2+3)mod8=5

(5+3)mod8=0

(0+3)mod8=3

Аналогичнолюбое числоможнополучить из5или 7. А вот из2уже нельзя:

(2+2)mod8=4

(4+2)mod8=6

(6+2)mod8=0

(0+2)mod8=2

Все,цикл замкнулся.

Чтомы здесь показали?Во-первых,правильность следствия опростых элементах. А во-вторых, правильность теоремы:циклическая группапорядкаm изоморфна некоторой аддитивной группе

Zm.

Тема «Сопряженные элементы вмоноидах и группах»

Все будет в этой теме:и обозначения,и определения,и утверждения,и теоремы.

Обозн. Пусть G– моноид,аS,S’– егоподмножества (обозн. S,S’≤G). Тогдамножествовсех обратимых элементов моноидаобозначаетсяIG.

Напомним,в моноиде необязательновыполняетсяобратимость каждогоэлемента,таквот вI обозначается именномножествотех элементов,у которых есть обратимые.

Опр. Элементы a,bмоноидаGназываются сопряженными в группе Н,где Н – подгруппа группы обратимых элементов моноидаIG (а при H=IG их называют простосопряженными),еслиg-1ag=b для некоторогоg изH.

Опр. ПодмножестваS,S’моноидаGназываются сопряженными в группе Н,где Н – подгруппа группы обратимых элементовмоноидаIG (а при H=IG их называют простосопряженными),если g-1Sg=S’для некоторогоg изH.

Обозн.

Вот такие новые обозначения. Между элементамистоят знаки «приближенноравно».

Замечание.Для коммутативногомоноида отношение сопряженности есть отношение равенства:

(g-1ag=(g-1g)a= a= b)

Другими словами:простоопределение отношениясопряженности. Отметим,чторавенствоверно толькодля коммутативногомоноида (коммутативность:xy=yx).

Утв.

1.Для любой группы Н отношение сопряженности вгруппе Н на моноиде Gесть отношение эквивалентности.

2.Если 2 подмножестваSи S’являются сопряженными в группе Н,тои порожденные ими множестватакже являются сопряженными вгруппеН. Кроме того,полугруппы, порожденные Sи S’являются изоморфными.

Доказательствопункта 1.

Покажем,чтоотношение сопряженности является отношениемэквивалентности,т.е. оноявляется транзитивным,симметричными рефлексивным(если удовлетворяет этим3свойствам– является отношениемэквивалентности). Оних можноподробнее прочитать на 5странице,или прямоздесь

– CopyPaste снова не подводит:

Рефлексивность требует выполнения условия: x?x is True. Простейший пример – вместо «?» подставляем равно.

Симметричность требует выполнения незатейливого условия: x?y => y?x.

Условия транзитивности тоже не отличаются сложностью: a?b & b?c => a?c

0.Единичный элемент измоноидаGявляется также единичнымэлементомвгруппе Н.

1.Рефлексивность:-любой элемент является сопряженнымссамимсобой (e-1ae=a)

2.Симметричность:=> g-1ag=b

Умножимслева наg,справанаg-1: gg-1a* g*g-1 = gbg-1

a=(g-1)-1bg-1

т.к. g-1 H, получили

3.Транзитивность:

g,h H g-1ag=b h-1bh=c h-1g-1agh=c (gh)-1a(gh)=c

Отсюда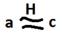 Пункт 1доказан

Докажемпункт 2.

Требуется показать,чтонайдется g,такой чтоg-1Sg=S’.

Покажем,чтополугруппы,порожденные этими множествами,также являются сопряженными вН, и они изоморфны,тоесть имеется биекция fg:S->S’, такая чтоfg(g’)=g-1g’g.

Предположим,чтоfg – не биекция,тогда:

fg(g’) = fg(g’’)

g-1g’g = g-1g’’g – запись изусловия

g’=g’’(т.к. g-1g=e)

Получили противоречие:2разных элемента не могут перейти в один => S->S’– биекция.

Будемсчитать,чтоg’ S, ипродолжимэтубиекцию.Тогдабиекцияfg может быть продолженадо биекцииполугрупп<S> и<S’>,т.е. построимбиекцию Ѱg:<S>-><S’>. Строитьбудемтаким образом, чтолюбомуслову wв алфавитеS(слововS –этопроизведениеэлементов изS) ставим в соответствиеэлементѰ(w)=g-1wg.Покажем, чтобиекцияѰg являетсягомоморфизмом,тоесть Ѱg(u*v)=Ѱg(u)*Ѱg(v). Действительно:

Ѱg(u*v) = g-1(uv)g

Ѱg(u)*Ѱg(v) = g-1ug*g-1vg =g-1(uv)g –т.к. gg-1=e

Итак, Ѱg:<S>-><S’>биекцияпоусловию,такжедоказали, чтоѰg являетсягомоморфизмом. Значит,группы<S>и <S’>изоморфны.

Другими словами:имели биективноеотображениеполугрупп, порожденныхSи S’. Построили биекциюи расширили еедобиекции<S>и <S’>. Показали, чтоэтогомоморфизм. Получилось, что построили биективный гомоморфизмполугрупп<S>и <S’>. Значит, эти группыизоморфны.

Если элементыa и bизмоноида G являютсясопряженными вН, причемэлементa имееттип(d,n), то и элементbимееттип (d,n).

Другими словами:сопряженныеэлементыимеютодинаковыетипы(тип (d,n) означает:gd=gd+n).