Разбор лекций

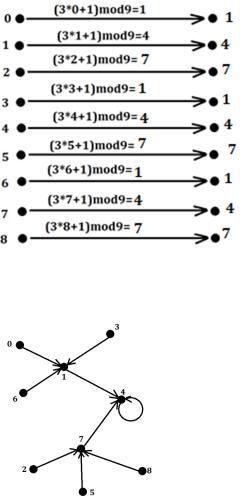
Вернемсяк нашимграфам ирассмотрим пример. Поопределениюграфа, у нас должно бытьg –некотороепреобразованиеэлементовмножестваХ вэлементы этого жемножества.

В нашем примеремножеством Хбудетмножествовычетов помодулю 9,а преобразованиеg выберемтакое:g=(3x+1).

Замечание:

1.Сначаланам нужнопосмотреть, вочтопереходиткаждый изэлементов множества. Будемизображать этострелками.

2.Нашепреобразованиеимеет вид:g=(3x+1). Номынаходимсявмножестве вычетов помодулю 9,т.е.каждоечислострогозаданоот 0до9. Ачтоделать,если в результатепреобразованияполучаетсябольшеечисло? Например, х=8,тогда g=(3*8+1)=25. Числобольше9иемунетместавнашем множестве, чтосним делать?Взять его помодулю9!Итакделатьвсегда, когданаходимсявмножестве вычетов помодулю 9и получаем число, большее9.Этоглавноеправиловычетов и егонужно знать.Тоестьпри х=8насамомделеполучаем: g=(3*8+1)mod9= 25mod9= 7.

Смотрим, вочтоперейдеткаждый элементмножества:

Теперь изобразим этонаодномрисунке. Расположениеэлементов неважно, затоочень важноколичествострелочек иих направление.

Получили оринтированныйграф дляпреобразованияg(x)=(3x+1) вомножествевычетов по модулю9. Развеэтосложно?:)

Приготовьтесь,сейчасбудет ещенесколько определений со сложными названиями. На самом делеони означаютсовсем очевидныевещи.

Опр. Полустепеньисходавершиныграфа– этоколичестводуг,исходящих изэтой вершины.

Другимисловами:это сколькострелочек выходитиз заданной вершины.

Опр. Полустепень захода–этоколичестводуг,которыезаходят в эту вершину.

Другимисловами:это сколько стрелочек входитвзаданную вершину.

Пример:

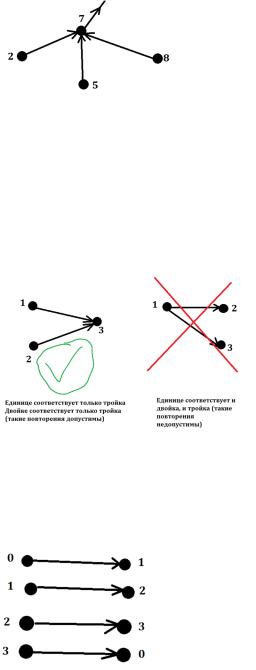
В семерку входит 3стрелкии выходит одна.Поэтому длявершины7полустепеньисхода равна1, полустепень заходаравна3.

Замечание.

В графелюбогопреобразованияполустепеньисходалюбой вершиныравна1.

Другимисловами: преобразование(поопределению)однозначнопереводит каждый элемент вочто-то:

Замечание: в графелюбогопреобразованияесть циклы,т.к.множествовершин конечно ввидуконечностимножестваХ.

Другимисловами: поопределениюграфамощность множестваХ равнаn,тоесть множествоконечно. Нотогдавсегданайдетсяциклический путьвграфе. Вот смотрите:

В таком случаеестьциклический путь: 3->0->1->2->3. Такжебывает,чтоэлемент простопереходит сам всебя.

Строгогодоказательстваэтогофактауменянет, но интуитивнопонятно, чтоэтоверно.

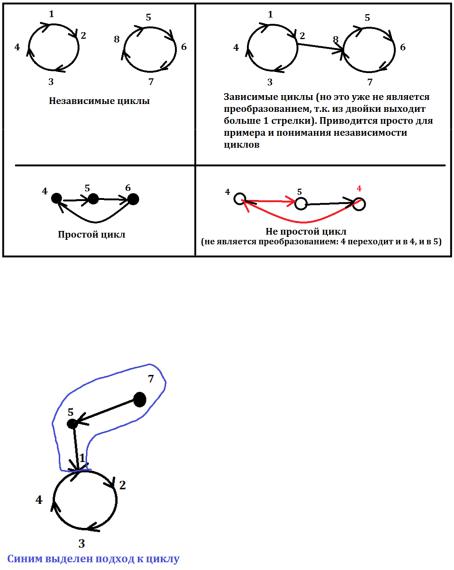
Замечание. Граф любогопреобразования содержитлишьнезависимыепростыециклы, количествоциклов равноr,и выполняютсянеравенства: 1≤r≤n,где|X|=n (n– количествоэлементов вомножествеХ).

Другимисловами: нуснеравенством совсем несложно: r=1в случаеединственного цикла, r=nв случае, когдакаждый элемент переходитсам всебя, тоестьграф представляет собойnпетель.

Теперь одругихновых словах. Независимыециклы –это циклы, вкоторых невозможно из одногоциклаперейти вдругой. Простойцикл –это цикл,каждая вершинавкотором встречаетсятолькоодинраз.

Из картинкипонятно, почему впреобразованиях неможет быть зависимых инепростых циклов.

Опр. Подходк циклу– этопуть,ведущий кциклу.

Предыдущеезамечаниеговоритнам отом, чтокаждый подход ведеттолькок одному циклу.Нельзяпотомиз 1циклаперейти вдругой.Этобылобы возможно, если бы допускалась степень исхода, равная2иболее(из одной вершинывыходитболее1 стрелки). Номы рассматриваемтолькопреобразования, гдестепеньисходастрогоравна

1.

Опр. Компоненты связностинеориентированногографа– этомаксимальноемножество вершин, гделюбаявершинадостижимаизлюбойдругой.

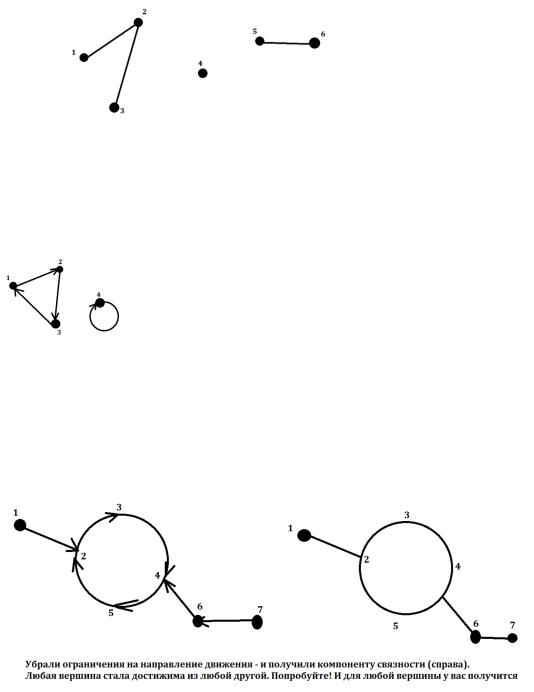
Пример:длявоттакогонеориентированногографаимеются3компонентысвязности:

1)1-2-3

2)4

3)5-6

Опр. Компонентасильной связности ориентированного графа–этомаксимальное количествовершин,гделюбаявершинадостижимаиз любойдругой. Или жепросто:циклыбез подходов кним.

Пример: аналогично предыдущему,тольконужноучитывать направлениестрелочек. Компоненты сильной связностидля рисунканиже: {1-2-3}и {4}.

Опр. Каждый изнезависимыхциклов вместесовсеми подходамикнему образуеткомпоненту связности в графе, полученном изориентированногографазаменой дуг наребра.

Другимисловами:дуги–это ребрасострелочкой.То есть есливзять независимый циклсо всеми подходамикнему истеретьстрелочки,получимкомпонентусвязности неориентированного графа. Напомним,компонентасвязности– этокогдалюбаявершинадостижимаизлюбой другой.

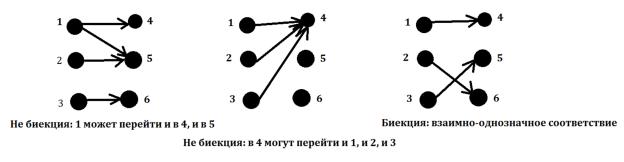
Опр. Полустепень заходакаждой вершиныравна1тогдаитолькотогда,когдаg– биективно.

Другимисловами: чтотребуетотнасбиекция(взаимно-однозначноесоответствие)?Чтобы каждыйэлемент однозначнопереходил вкаждый,причем этосоответствиеопределено однозначно. Посмотритенакартинкуниже, ивы поймете, почему изкаждойвершиныможет выходитьтолько1стрелочка, и заходитьтолько1стрелочка.

Опр. Цикловаяструктурапреобразованияg –это запись вида:

G(g) = (l1[k1]; l2[k2]; …;ln[kn]), где:

|X|=n,

Г(g) –граф преобразованияg – содержитki циклов,причем цикл ki имеетдлинуli, атакжеi=1..m

и l1<…<ln.

Другимисловами:этотаблица, вкоторой записаны длиныциклови сколькораз они встречаются. Ну действительно,li –длинацикла, ki – количествоцикловтакойдлины,аесли сложитьвсеki (количествациклов разных длин),тополучимколичествовсех циклов.Длины расположены в порядкевозрастания. Мы ещепостроим такую структуру.

Это так,т.к. всего вершинn,и большеn получитьсянеможет

Замечание:

∑=n g-биективно.

Посутив этихдвух замечаниях мы считаливершины нациклах (аграф биективного преобразования– всециклыбез подходов).Действительно,длинацикла–этоколичество ребер, составляющих этотцикл, аk–количествотаких циклов.ПроизведениеL*Kдаетколичество вершин в этомцикле, а ∑ – количествовершин вовсех циклах. Этасуммаравнаnтогдаи толькотогда,когдаграф состоиттолькоиз циклов(каждая вершинаучаствует вкаком-то цикле). Аэтовыполняется толькотогда, когдаграф построен длябиективногопреобразования. Строгогодоказательстваэтогофактауменянет, но, темнеменее, этотак.

Утв. Пустьg –некотораяподстановка(т.е.биективноепреобразование)n-множестваХ, имеющая циклическуюструктуру:

G(g) = (l1[k1]; l2[k2]; …;ln[kn])

∑=n (т.к. преобразованиебиективно).

Тогдаколичество подстановокмножестваХ, имеющих ту жециклическую структуру, чтои g,

(Другимисловами– количествотаких подстановок, прикоторой получаетсятакоеже количествоцепейтаких жедлин, какпри подстановкеg).

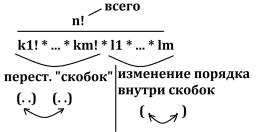
Доказательство. Рассмотримпример,демонстрирующий верность этого утверждения. Работатьбудем намножественатуральныхчиселот 1до14.

Пустьg: N14->N14 (каждомуэлементуизN14 ставится в соответствиеэлементтакжеизN14).

Пустьgимеетцикловую структуру:

C(g) =(2[2], 3[2], 4[1]). Тоесть граф подстановки gвключаетдвацикладлины 2,двацикладлины3 и 1циклдлины 4.Наглядноэтовыглядиттак:

(. .)(. .)(. . .)(. . .)(.. . .)

Имеется14! Способов расставить 14вершин наэтипозиции.Что мы приэтом учитываем лишнее?

Во-первых, воттакиеподстановки являютсяодинаковыми:

Почему? Впервом случаенаписанопоменятьместами 1и3, 2и4. Вовтором случае: 3и 1, 4и 2.

Скольковсеготаких «лишних»подстановок?Мыпоняли, чтоесли поменятьместами подстановкиодного порядка, ничего неизменится. Аколичествоподстановокодного порядка равноki (гдеi –порядокподстановки). Теперь внимание: скольковозможно перестановок k элементов?Правильныйответ –k!Поопределению факториала. Аесли естьпонесколько перестановок каждогопорядка?Скажем, 5подстановок из 2элементов и7 подстановок изтрех? Количествомусорав первом случае5!, вовтором –7! Тутколичествоэлементовневажно(это мы учтем вследующем пункте). Покаважнотолькоколичествоподстановок разныхпорядков.

В общем случаенаберетсяk1! * …* km! «лишних»подстановок.

Во-вторых, одинаковыми являютсяитакиеподстановки:

Ну правда, сначалапоменять местами 1и 3, потом2 и 4, или наоборот– ничегонеизменится.

Скольковсегоунасподстановоквкаждой скобке?Правильно,li. Уэтихскобок l=2, у скобок из трех элементов l=3ит.д.

Ивот унас2скобкипо2элементаи 1скобкаиз3элементов.Элементывнутрипервой скобки можнопоменятьместами2 способами, внутри второй тоже, внутритретьей – 3способами.

В общем случаеполучимl1*…*lm.

Получили:

Тема«Алгебраическиеосновы»

Ещеоднатема,нетакаяхорошая, как графы.Помните, в самом началеяцелую страницу рассказывал промоноидысгруппами?Воттут намвсеэтопригодится. Еслизабыли –советую повторить страницу 2.

Опр. Идемпотентом полугруппыGназываетсяэлемент i€G,такойчто i*i=i.

Множествовсех идемпотентовполугруппы GобозначаетсяE(G).

Опр. ПолугруппаGназываетсяунимпотентной, если в нейсодержитсяровно 1идемпотент: |E(G)=1|.

Замечание. Группасодержит единственный идемпотент, совпадающий сединичнымэлементом.

Доказательство.

1.В группеесть единичныйэлемент: e*e=1

2.Пустьимеетсяещеi,такой чтоi*i=i.Вспомним, чтов группекаждыйэлементимеем обратный. Тогда:

i*i=i

i*1=1

i(i*i-1) = (i*i-1) но(i*i-1) = e i*e=e

отсюдапоопределениюединичного элементаi=e(x*e=y => x=y).

Опр. Элементg изполугруппы Gназываетсярегулярным, еслив Gнайдетсяx, такойчтоg=g*x*g.

Замечание. Любойобратимыйэлементмоноидарегулярен (напомним –моноиддопускает существованиеобратногоэлементанедлявсех элементов).

Ну действительно, еслиу элементаестьобратный,тобудет выполняться соотношение:g=g*g-1*g

Опр. Еслиэлементg регулярен (т.е. существует х: g*x*g=g), тоэлементы g,g’изполугруппы G

=′

связаны соотношениями: = . Любыедваэлемента, удовлетворяющиеэтим соотношениям, называются взаимно-инверсными.

Другимисловами:тутпростовводитсяопределениевзаимно-инверсных элементов: онитакими являются, еслиудовлетворяютуказанномусоотношению.

Замечание. Любые2взаимно-обратныеэлементамоноидавзаимно-инверсны.

Опр. ПолугруппаGназываетсярегулярной, есливсеееэлементы регулярны.

Опр. ПолугруппаGназываетсяинверсной, есликаждый ееэлемент имеет единственный инверсный.

Тема«ГрафыКэлиполугруппигрупп».

Здесьтожевам пригодятся знаниямоноидов,групп ит.д.Занимиможноотправитьсянастр.2

Опр. Гомоморфизмом полугруппы(G, *)в полугруппе(G’, x) называетсяотображение:

φ: G->G’:

φ(x,y) = φ(x) x φ(y) для любых x,y из G.

Напомним, полугруппа обозначается в скобках: название полугруппы и относительно какой операции она задана. (G, *) – полугруппа G относительно операции умножения. (G’,x) – полугруппа G’ относительно некоторой операции «икс».

Опр. Изоморфизм полугрупп – биективный гомоморфизм полугрупп.

Другимисловами:когдасоответствиеφ: G->G’ является взаимно-однозначным. Только недавно разбирали, скопирую сюда картинку определения биекции.

Опр. Гомоморфизммоноидов G->G’ –этогомоморфизм полугрупп,такой,чтоединицамоноидаG отображаетсяв единицумоноидаG’.

Другимисловами: всетот жегомоморфизм соднимдополнительным свойством.

Опр. Подполугруппой полугруппыG называетсяееподмножество, являющеесяполугруппой.

Другимисловами: здесь ужевсенеочевидно.Поэтому будем разбираться.Сновапрямона практике.Пустьу насесть полугруппаGи ееподмножествоG’.ОбозначаетсяG’ G,G – полугруппа. Требуется проверить,являетсялиG’ подполугруппой.

Ачтотребуетполугруппа? Замкнутостьи ассоциативностьотносительновыбраннойоперации. Так какмы рассматриваем подмножествополугруппы G,тоассоциативностьпроверять не нужно: т.к.G-полугруппа, операцияужеассоциативна, и ееассоциативностьникуданеденетсяв некотором подмножествеполугруппыG.Получается, нужно проверитьтолькозамкнутость.

Ачтотакоезамкнутость? Берем 2элемента изG’,применяем кним операцию (относительно которой рассматриваетсяполугруппа) и смотрим,невышлилимы заграницы G’. Еслиза границы G’ выйтинеполучитсянидлякаких элементов, тооперациязамкнутаотносительноG’, и G’являетсяподполугруппойполугруппыG.

Опр. ПодмоноидмоноидаG сединичнымэлементом eявляетсяегоподмножеством со свойствами:

1.Замкнутость: G’ xG G’ (G’ замкнуто)

2.В G’входит e:e G’

Другимисловами: просто определениеподмоноида.

Опр. ПустьG –полугруппа,и есть еенекотороенепустоеподмножествоS:S G,S≠

Тогда<S>- будем обозначать наименьшуюподполугруппуполугруппы G,содержащую множество Sи состоящую извсех слов в алфавитеS.

Другимисловами:Многослов,анаделепросто. Пусть унасестьG={g1…g100}. Возьмемпервые три элементаи составиммножество S={g1, g2,g3}.

Тогдавомножестве, порожденномS, находятсяэлементыg1,g2, g3 и всевозможные произведения этих элементов:g2g3,g1g2 ит.д.

Понятно, что Gтакжесодержитвсевозможныекомбинации(g2g3,g1g2 ит.д.),т.к. оназамкнута, а значит гарантируется, что при операции умножениялюбых ееэлементов мы невыйдем за пределы группы (поопределениюдлялюбых x,y G =>x*y GдляполугруппыG).

Получили <S> -полугруппу, порожденную S.

Наэтомоптимистичномэтапеплавнопереходим кследующейлекции. Онаокажетсянетакой прозрачной, как предыдущая:некоторыефакты приводятсябездоказательства, анекоторые– дажебез примеров. Их мыразберем в разделесзадачами. Несказал бы, что этоплохо. Вспомните хотябылемму Анселя. Излекциибыло непонятночутьболее, чем ничего.Затоесливы уже успели прочитать семинар,тоузнали, чтов этойлемменетничегосложного, апользоваться ей легкоиприятно.Поэтому–давайтеначнем.

Опр. Если вSвходиттолько1элементg (т.е. S={g}), тополугруппа, порожденнаяg(а, возможно, и группа–зависит отконкретнойзадачи), называетсяциклической. Такжеможно сказать, что элемент gпорождает циклическуюгруппу/полугруппу <g>.

Другимисловами: еслиполугруппа/группапорожденаодним единственнымэлементом,тоона являетсяциклической. Прото, чтотакоепорожденная группа, можнопрочитатьв предыдущем определении. Примертожебудет, ночуть позже, поканемногоопределений.

Опр. Если<S>=G,тоговорят,что sпорождает G.

Другимисловами: взяликусочек из группыG:

Чтобы построитьгруппу,порожденнуюэлементами из S,нампридетсявключитьтудавсе возможныепроизведенияэтихэлементов.Атеперь – внимание. Еслипослевключения всех такихэлементовмыполучили исходную группу G,то можносказать, чтоSпорождает G.

Вот вампример:

Чтобы построитьгруппу,порожденную S,нампридетсявключитьвсевозможныепроизведения элементов x1иx2. Тоесть<S>={x1, x2, x1*x2}. Нополучилась вточности группаG!Именнопро такуюSговорят, чтоонапорождает G.

Замечание: системаобразующихэлементов определенадляGнеоднозначно.

Другимисловами: никтонезаставляетнасвзять именнокакие-токонкретныеэлементы. Если нам удалось взятьтакиеэлементы,чтогруппа, порожденнаяими,будет равнаисходной– все хорошо, нашазадачавыполнена.

Замечание: в будущем частобудетвстречатьсясочетание«элементg в системеобразующих». Это означает, чтоесть наборэлементов, которыепорождают какую-тогруппуили полугруппу. И вот g–это одинизэтихэлементов.Все, теперьможнодальше.

Опр. Длинаэлементаg(из конечнойполугруппы G) в системеобразующихS (обозначаетсяl(gS)) называетсядлинакратчайшего словавS, равногоg.

Другимисловами: опять страшноеи непонятноеопределение. Насамомделеонолишьговорито том, чтоеслиS порождает G,толюбой элемент изGможнопредставить какконечное произведение элементовизS. Таквот, длина наименьшегословаизS,образующегоg, называется длиной l(gS).

Ну действительно,изчегосостоит группа,порожденная элементами изS?Извсех этих элементов и всевозможных их произведений. А S,вообще говоря,кусочекгруппы G. А таккакG – группа,то она замкнута. Тоесть при умножении любыхдвух элементов группы Gмы гарантированно получимэлемент изэтой группы. Получается,чтов группу Gвходят все возможные произведения этих элементов. Теперь должнобыть понятно,почему любой элемент изGможнопредставить как конечное произведение элементов изS. А именно,этоследует из2пунктов:

1.Т.к. Sпорождает G,то<S>=G

2.G(поопределениюгруппы) включает всевозможные произведения своих элементов.А <S> тоже их включает,поопределениюпорождения.

Получили,что<S> состоит извсех элементов группы G,причемлюбой изних можнополучить каким-либоумножениемэлементов изS(которые порождают G– тоесть как-тоумножая их, можнополучить любой элемент изG– включая в<S> такие произведения,мы расширяемся доG).

Опр. Длиной покрытия непустогомножестваX (являющегося подмножествомполугруппы G) в системе образующихS(обозначается l(X,S)) называется величина:

L(X,S) = max(l(gS)).