Разбор лекций

3. Транзитивность (еслиx y &y z,то x z)

Также напомним:f ≡Ψ означает, чтоΨ(х)=f(g(x)) – существует некоторая перестановка g.

Лемма Анселя.

РешеткаVn разбиваетсянаb)n_ цепей сосвойствами:

1.ξ (n-2p) = Cnp - Cnp-1, 0≤p≤[n/2], где минимальный элемент каждой такой цепи есть вектор веса p, а максимальный – вектор веса n-p.

2.Если (a1, a2) и (a2, a3) – дуги диаграммы решетки Vn, принадлежащие цепи длины n- 2p, то элемент b, образующий вместе с элементами a1,a2,a3 подрешетку решетки Vn, изоморфную решетку V2, принадлежит цепи n-2p-2.

Следствие.

ШиринарешеткиVn равнаb(n).

Другимисловами:как ужесказал ранее, янебуду разбирать этулемму–листы вWord закончатся. Даи посленескольких строчек чтенияподобной информацииэтотдокументбудет закрыт иотправленв Корзину.Всеженашацель–разбори пониманиетого, чтоздесь происходит. Стакойлеммойэтобудет оченьсложно. Поэтомудавайтетак:если онавам потребуется, вы обязательноееразберите. Достаточно выделить4-5часов, и у васвсеполучится. Практическоеприменениелеммы вынайдетев разборезадач.

P.S. Какой-тобестолковыйпараграф получился:)Парапростейших определений, потом –БАХ! – и леммаАнселя.Почтикак накартинке. Нуиладно, криптографы инестаким сталкиваются.

Тема«Решеткаделителейнатурального числа»

Темасостоит изтрех утверждений,дваизкоторыхпредусматриваютдоказательства.

Опр. Пустьканоническоеразложениечислаn впроизведениестепеней простыхделителейp1…ps имеет вид (ki>0– кратностьделителяpi):

N= p1k1 * …* psks

Другимисловами: числопредставили ввидепроизведенияпростыхмножителей, возведенныхв некоторыестепени. Тут всепонятно.

Утв. ЕслиD(n) –решеткаделителей, то:

|D(n)| =∏ ( +1)

L(D(n)) =k1+…+ks

Чтотут сказано?Здесьпоказано, как вычислить размерность решеткиD(n)и еедлину.Повот такимформулам. Сначалаэтиформулы кажутсяневзрачными, нокриптоаналитикиговорят, что именноих знаниеотличает человекаотрыбок.Азнаниедоказательстваэтихформул,в свою очередь, отличаеткриптографов отлюдей. Поэтому доказательствообязательнорассмотрим.

Доказательство.

Если dделитнацелоn, иbтоженацело делитn,то:

max(d,b)=НОК(d,b) D(n)

min(d,b)=НОД(d,b) D(n).

Небуду разводитьбольшойлишний абзац – здесьвы всезнаете. Max иmin –введенныенами обозначения, они ниоткуданеследуют,этомыихтак определили.Вспомните, что такоеНОКи НОД. Вспомните, что D(n) –решеткаделителейчислаn…Поняли?Давайтедальше.

Какой вид имеетделитель dчислаn?Воттакой: d=p1q1 * …* psqs, где0≤qi≤ki,гдеi=1..s.

Итутничегосложного.Вспомним,что N= p1k1 * …*psks. Амы берем кусочек этой цепочки. Понятно, что этотожебудетделителем числа.

Ну например: 20=5*2*2. Возьмем кусочек 5*2=10.Он является делителемчисла20.

Чему равноколичествовсех возможныхделителейчислаn? Давайтепосчитаем, унасдляэтого ужевсеесть. Общий видтакогоделителямыполучили ранее:

d=p1q1 * … *psqs, где0≤qi≤ki,гдеi=1..s

Чтотут написано?Написано, чтовозможноs множителей, укаждогостепень от 0доki (т.е. в каждом случаевозможнастепень от0доki). Отсюдаполучаем: |D(n)| =∏ ( +1).

Теперь разберемсясдлиной цепи.Понятно, чтосамаядлиннаяинеуплотняемая цепьполучится, если в неевключить абсолютновседелителичисла. Ну действительно, есликаждоезвено добавляет один-единственный делитель,тоуплотнитьдополнительноееникак неполучится. А сколькоунасвсего делителей?K1+…+ks. Почему?Смотрите.Числоn представимоввиде:

N= p1k1 * …* psks

Инам нужнонайтидлянеговседелители.Каквыглядитэточисло напростомпримере?

100=25*52.

Акакиеу негоделители?Давоттакие:

100=24*52.

100=23*52.

100=22*52.

Ит.д.

Тоесть 25 дает 5разныхделителей, 52 -еще2 делителя. Меняемстепень–меняется делитель. А количествовсех возможныхтакихспособов и естьдлинацепочки.

L(D(n))=k1+…+ks.

Замечание. Если bделит нацелоn,тоD(b)– подрешеткарешетки D(n).

Опр. Натуральноечислосвободноотквадратов, если ононеделитсянаквадратлюбогопростого числа(неимееткратныхделителей).ОбозначаетсяD1(n).

Другимисловами: воттутуженевозможнотакоеразложение: 100=25*52 – кратныемножители недопускаются. Авоттакое: 34=2*17–вполнеподойдет.

Утв. D1(n)= D(p1…ps)≡Vs.

Утв. Еслив разложении [N=p1k1 * …* psks ]

s=1, то h(D(n))=1;

s>1и 1=k1=…=ku<ku+1≤…≤ks, где0≤u≤s (u=0приk1>1, u=sпри ks=1), то

b’(s)+b(s)-Cu[s/2]≤h(D(n))≤∏ ( +1).

Доказательствоздесьдостаточносложное, поэтому покаегопропустим. Если разберу доконцаи появитсявремя – обязательнонапишу егоразбор.

Апокаперейдем кследующимтемам. Несколькоближайших мнеудалосьразобрать очень хорошо– гораздо лучше, чем предыдущие. Поэтому обещаю интересныеописанияи максимум примеров. Поехали :)

Тема«Решеткаразбиениймножества».

Казалось бы,можетлибытьчто-тоновоеврешетках разбиений? Авот иможет. Например, новыеопределенияиновый способдоказательстватеорем. Вытакогоещеневидели.

Опр. Rn –множествовсех разбиений N-множества(множествамощностиN) нанепустые непересекающиесяблоки.

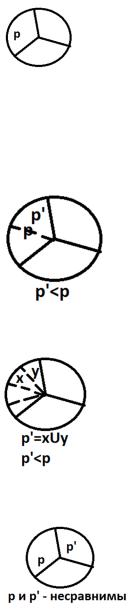
Введем наRn частичный порядок: еслиесть2разбиения ри р’из Rn,тоотношениеp≤p’ выполняетсятогдаитолькотогда, когдакаждый блок разбиения p’ естьлибоблок разбиенияр, либообъединениенескольких блоков разбиенияр.

Чтоздесь написано?Вотчто:пусть унасестьмножествомощностиN.Оновыглядиттак:

Разбиваем егонанесколькочастей, и одноиз разбиений обозначаем р:

Читаемдальше: отношениеp≤p’ выполняетсятогдаитолькотогда, когдакаждый блок разбиенияp’ естьлибоблок разбиения р,либообъединениенесколькихблоковразбиенияр.

Тоесть еслимыхотим выбратьразбиениер’, котороеменьшеилиравноужезаданному р,мы должнывзять кусочек иликусочки отэтогор:

Или разбить наещебольшекусочков и взятьнесколькоиз нихкак р’:

Авотдругиекусочки (неиз р) брать нельзя–онибудутнесравнимыср:

Авообще, чтотакоеRn?Этомножествомощностиn, накоторомзадано отношениечастичного порядка. Почему частичного? Потомучтоневсеразбиенияможносравнивать,этопоказано выше. Так чтотакоеRn послетого,как онаудовлетворяет этисвойствам? Даэтожерешетка!

Рассмотрим особенностиэтой решетки.

1.Нуль решетки 0Rn. –это разбиениенаnодноэлементныхблоков. Тоестьтаких блоков,в каждом изкоторыхнаходитсятолько1элемент. Их числоравно n,т.к.всегоэлементовn, и мыразбиваем ихнаблокитак, чтовкаждомблокенаходится 1элемент.Другими словами 1 блок– 1элемент. Тогдаnэлементов –nблоков.

2.Единицарешетки1Rn – этосамомножествомощностиn.

3.Атом решетки– разбиения, вкоторых (n-2) одноэлементныхблокаи 1двухэлементный блок.

4.Коатом –разбиениеn-множестваровнона2блока.

Какможно заметить,здесь атомыикоатомы– неконкретныеэлементы, аспособы разбиениямножеств.

Перед началом следующегоопределенияхочетсясказать, чтоиногдапростыевещиназывают сложнымиименами. Незнаю,почему. Апотомнехорошиелюдипугаютостальныхдлинными словами набуквуС. Но насамомделеонидажепроще, чем короткиеслованабукву…. Вот смотрите.

Опр. ЧислоСтирлингавторогорода–этоколичестворазбиений n-множестванаk непустых блоков.ОбозначаетсяS(n,k).

Вот ивесь смыслэтогочисла, котороетолько насловах – числоСтирлинга.

Хотитекартинку? ТогдаPaint идетк вам:

Теперь узнаем, как вычислять числоСтирлигна. Формуланесложная, адоказательство интересное. Вот правда. Недумалраньше, чтоонитакими бывают: обычноони состоятиз огромногоколичестванеслишкомприветливых формул. Здесь жевсе, какговорится, по полочкам.

Утв. S(n,k) =S(n-1, k-1) + kS(n-1,k).

Доказательство.

Будем искатьколичестворазбиениймножествамощности nнаkблоков. Возьмемв этом множественекоторыйэлементz изафиксируем его. Воттак:

Ибудемрассматривать всеразбиенияотносительноэтогоэлемента.

Попробуем ответитьнавопрос: какиевозможны случаи для блока, вкоторыйвходит z? Возможно2случая: вэтомблокенаходитсятолькоэлементz, илитамнаходитсяэлементz и еще некоторыеэлементы.

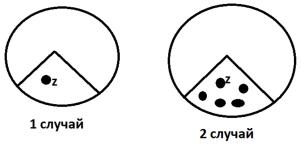
Рассмотрим 1случай:{z} образует отноэлементный блок разбиения.

Всегов множествебылоnэлементов,взялиодин(z), сколько осталось?Правильный ответ: (n-1).

Мы искали количествоспособов разбиениянаkблоков. Одинблок(сэлементом z) ужеесть. Сколькоблоков осталось заполнить?Правильныйответ:(k-1).

Итак, нужнозаполнить (k-1) блок элементами,количествокоторых (n-1). Другимисловами: найтиколичествоспособов наполнить (k-1) корзину яблоками,которых (n-1) штук.

Подождите, ненужносразу открыватьтеорию вероятностей. Вспомнимопределение, которое былопару строчек назад:ЧислоСтирлингавторогорода– этоколичестворазбиенийnмножестванаk непустых блоков.ОбозначаетсяS(n,k).

У нассейчасn-1элементи k-1блок, поэтому количествотаких разбиенийравноS(n-1, k-1).

Итак, первый случай готов: количествовсевозможных разбиений, прикоторыхэлементz образует одноэлементныйблокразбиения, равноS(n-1, k-1).

Рассмотрим 2случай:вблокесэлементом zнаходитсянетолькоz,ноинекоторыедругие элементы.Определимколичествовсевозможныхразбиений притакомусловии.

Здесь сделаем немногопо-другому: возьмемэлемент zи удалим егоизмножества. Былоn элементов, осталосьn-1. Иихнамнужнораспределитьнаkблоков.Сколькими способамиэто можносделать?Прямопоопределению:S(n-1,k).

Атеперь вкаждыйиз полученныйблоковможнодобавлятьэлементz. Этоможно сделать k способами, т.к.всегоу насkблоков.

Второй случай готов:количествовсевозможных разбиений, прикоторыхэлементz образует многоэлементныйблок разбиения, равноk*S(n-1,k).

Получили:S(n,k)= S(n-1,k-1) +k*S(n-1, k).Доказано.

Докажем ещеодноутверждениедляS(n). Способдоказательстватакой же, но сампроцессеще болееинтересный.

Утв. S(n,k) =∑ ( −1) * S(r, k-1).

Доказательство.

Сновабудем считатьколичествовозможных разбиений n-множестванаk непустых блоков.

Как ив предыдущемдоказательстве, зафиксируемнекоторый элемент zи будемрассматривать всеразбиенияотносительно него.Возможныеслучаи – блок, вкоторыйвходит z,состоиттолько из элементы z,илисостоитиз 2элементов, илииз3, или… изn. Новернемся к началу.

1.Пустьсам элемент zобразует одноэлементныйблок разбиения.

Количество всевозможных разбиений притакомусловии мы ужесчитали впредыдущем доказательстве: оноравноS(n-1, k-1).

2.Пустьэлементz входитвдвухэлементныйблок (состоит изэлементаz и ещеодного элемента)

Важнопонять,какпроизошел этотпереход. Былблок, вкоторомнаходилсятолько элемент z.Мывыбраливторой элементидобавили кнему.Сколькими способамиможно былодобавитьэтот второй элемент?Правильныйответ –n-1способами,т.к.всего элементовn, аодин (z) ужебылзафиксирован.

Отлично!Осталосьn-2нераспределенных элемента, которыенужноразбитьнаk-1блок (т.к.дваэлементаужевыбрано, иони составляютодинблок).

Тоесть количество всевозможных разбиенийприусловии, чтоz образует двухэлементныйблок,равно(n-1)*S(n-2, k-1).

3.Пустьэлементz входитвтрехэлементный блок (блок состояитизэлементаzи еще2 элементов).

Ивновь одинэлемент(z) зафиксирован, осталосьn-1элементов. Итеперь нам надо

Итак, выбрали 3элемента(z иеще2шт), сформировали 1блок. Элементов стало на3 меньше, блоков –на1.Количествовозможных разбиений:S(n-3, k-1).

Тоесть количество всевозможных разбиенийприусловии, чтоz образует

4.Случай n. Пустьz находитсявn-элементноммножестве. Тоестьэлементz иn-1других элементов. Новедьв множествевсегоnэлементов? Неужели полноенепонимание? Нет, здесь всехорошо. Давайтесначалазапишем формально,и затем всеподробнообъясню.

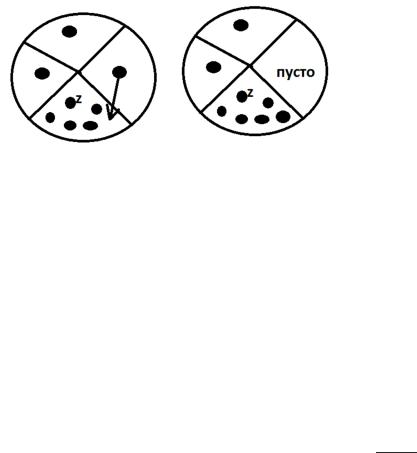
Рассуждаем как раньше: zобразует n-элементныйблок,причем один изэлементовуже задан (z). Сколькоосталось? N-1. Сколькими способамиможновыбратьn-1элементизn-

1элемента?Правильныйответ: ( −− 11) – эточислосочетаний, анедробь.

Итак, в одномблокеоказалосьn элементов (z иещеn-1элемент). Теперьнужно разбить оставшиеся0элементовнаk-1блок. ЭтоможносделатьS(0, k-1) способами.

Получаем окончательно:( −− 11)* S(0, k-1).

Чтозаабсурдздесьпроисходил? Давайтеразбираться.

Чтомыделали?Сначаламы предположили,чтоблок, содержащий z, включаеттолько одинэлемент –сам z.Потом –дваэлемента(zи ещечто-то).Потом –триэлементаит.д. Тоесть чтопроисходит?Мы постепенно увеличиваем блоксэлементом z,приэтом на остальныеблоки остается всеменьшеэлементов.Аразбитьмыдолжны по-прежнему на k блоков! Ивот наступаеттоткритическиймомент, когдавблокесэлементом z находитсянекотороеколичествоэлементов,авовсех остальных k-1блоках – поодному элементу. Итеперь если ещехоть одинэлементперебросить в блок сэлементом z,то какой-тоблок окажетсяпустым,что неразрешенопоусловию (ищем разбиения наk непустых блоков).

Акак отреагирует наэтонашаформула?Абсолютнокорректноотреагирует!Потому что S(n,k)=0, еслиn<k. Ну невозможноразложить4 яблокав 5корзин. Иснекоторогослучая этислагаемыебудут просторавняться нулю.

Тоесть всеунасправильно,и взаписи ( −−11)* S(0, k-1)нет никакой ошибки –онаравна нулю,т.к. невозможнораспределить 0элементовпоk-1блокам.

Обобщим полученную информацию.

Если z образует одноэлементныйблок,токоличествовариантов равноS(n-1,k-1). Если 2-хэлементный блок,то(n-1)S(n-2, k-1) вариантов

Опр. Bn =∑ ( , ) называетсячислом Белла. То естьколичествовсех возможных разбиений множества.

Другимисловами:тутнаписаноBn =S(n,1) +S(n,2) + …+S(n,n) –количестворазбиений на1блок,на2блока,на3блока… наn блоков –тоесть количествовсех возможных разбиений.

Утв. Bn+1 =∑ ( )*Bk.

Доказательство.

Будем считатьколичествовсех разбиений множествамощностиn+1.Обратитевнимание

– здесь всегоn+1элементов,анеn.

Как ив предыдущихдоказательствам,возьмемнекоторыйэлемент zи зафиксируемего. Былn+1элемент, один зафиксировали -осталосьn элементов.

Исновавозможно несколькослучаев: zнаходитсяв одноэлементномблоке, в двухэлементном ит.д.

1.Если z находитсяв одноэлементномблоке, токоличество всевозможных его разбиений равноBn. Ничеголишнего, просто определениечислаБелла.

2.Если z находитсявдвухэлементномблоке. Фиксируем z иподбираем ему второй элемент. Этоможносделатьn способами (т.к.всегоэлементов здесьn+1). Забрали 2элемента(z и ещекакой-то), получили 1блок.Былоn+1элементов, остался n-1элемент.

Получаем, чтов случае, когдаzнаходитсявдвухэлементномблоке, количество всевозможных разбиений равноn*Bn-1.

3.Если z находитсявтрехэлементном блоке. Фиксируем z иподбираем ему второй и

третийэлементы.Этоможно сделать(2) способами. Былоn+1элементов, забрали3

элемента. Осталосьn-2элемента.

Получаем, чтов случае, когдаzнаходитсявтрехэлементномблоке, количество

всевозможных разбиений равно(2)*Bn-2.

Обратитевнимание– заколичествомблоковмытут неследим, ононезадано!Число Белласчитает всевозможныеразбиениянаблокивсех возможных размеров, обратитенаэтовнимание.

4.Если z находитсявблокемощностиj,тоаналогичнополучаем:

( − 1) – способов «добора»j-1элементов домощностиj(в началезадантолькоz) Bn+1-j – разбиенияэлементов,невошедших вблок сz.

Получаем: ( − 1)*Bn+1-j.

Получаем:

Bn+1 =∑ ( −1) * Bn+1-j. – сумма, т.к. zможетоказатьсявблокелюбоймощности.

Преобразуем:

Доказано.

Тема«Графыпреобразований»

Начинаем новую большуютему –графы. Тут нам пригодится(насамом простом уровне) немногологики–графы прощесначалапонятьнаинтуитивном уровне, тогдавсеопределения и формулировкипокажутсяпочти очевидными.

Опр. Еслиg– преобразованиемножестваX (g: X->X, элементуиз Х ставитв соответствиетакжеэлементиз Х)и |X|=n.Тогдаграф преобразованияg – этоnвершинный ориентированный граф.ОбозначаетсяГ(g) смножествомвершин Хи множествомдуг(x, g(x)).

Другимисловами: пустьимеетсямножествоХ сколичествомэлементовn. Функцияg выполняетнекоторыепреобразованияэлементовиз Х. Причемкакначальный,так и полученный врезультатепреобразованияэлементы принадлежат Х. Тогда преобразованиеg можнопредставить ввидеориентированногографасn вершинами.

Давайтенемногоотвлечемсяи вспомним,чтотакоеориентированный граф и (внезапно) множествовычетов.Подождитеперелистывать страницу: вспомните, сколькобылоопределенийсосложныминазваниями,которыенасамомделе означают самыепростыевещи(числаСтирлинга,например). Вот здесьбудеттак же:)

Ориентированныйграф –этотот жеграф, который мырассматривали ранее(в

разделе«ч.у.м.»), носуказанием направлений пути.

Вот здесь нарисовано, чтоиз 1в 2перейтиможно,аиз 2в 1–уженет.Все, в остальномэтотакой жеграф.

Множествовычетов помодулю– звучит странноинепонятно, нонаделеэтоне сложнеемоноидатаблицы истинности. Можнодать огромноеколичество определений, общих формул,никтоничегонепоймет, ипойдет слух, чтопонять вычеты сложнее, чем смысл жизни. Аможнопривести простой ипонятныйпример, чтомыи сделаем.

1.Чтоозначает «числопомодулю9»? Этоостатокотделенияэтогочислана9. Все, ничегобольше!Пример: 19помодулю9равно1. 20помодулю9равно2. Записывается:

19mod9 = 2 20mod9 = 2

2.Тогдачтотакоемножествовычетов целых чиселпомодулю 9? Этомножество всех целых чисел, взятых помодулю 9:

0mod9= 0 1mod9= 1

…

8mod9= 8 9mod9= 0 10mod9=1

Ит.д.

Чтомыделали?Брали всечислаисмотрелиостаток отделенияна9. Тоесть множествовычетов целых чиселпомодулю 9 состоит изчисел {0..8}. Все:) Посмотрев следующийпример, выокончательноразберетесь свычетами.