Разбор лекций

подмножеством{i1…ij},где i=1…p– индексы системы образующих элементов сосвойством gij(x)=y,где j=1…s.

Сейчасстанет понятнее. Вот примеркусочкаграфа ГS для S={g1,…,gp}.

Рисунокрасшифровывается так:

1.х и у соединены – значит,имеются преобразования,переводящие х в у

2.стрелкапомечена (1,3)– значит,что: g1(x)=y

g3(x)=y

Замечание.Наличие пути изх в у в графе ГS(x) равносильноналичиюпреобразования g(x)=y.

Также обратимвнимание,чтох и у не обязательнодолжны соединяться одной стрелочкой. Может быть и более длинный путь:

Вот здесь х и у не соединены стрелочкой,однакоg2(g1(x))=y. Преобразованиеg2g1 также принадлежит G,т.к. этогруппа,где соблюдается замкнутость.

Вывод:если путь их одной вершины в другуюесть,ноон не прямой,тонайдется преобразование, переводящее х ву,являющееся композицией нескольких преобразований.

Опр. Пусть Н – группа подстановокмножестваX. Преобразования g,hизП(Х) называются сопряженными в Н (или подобными вН),если вH найдется б,такой чтоg=б-1hб. ЕслиH=S(X),то название сокращается до«простосопряженные».

Другими словами:все просто: если в Н такой элемент найдется,топреобразования называются сопряженными в Н.

Замечание. Отношение подобия относительнолюбой группы Н,заданной на П(Х),является отношениемэквивалентности.

Другими словами:если отношение подобия заданонаП(Х),тооноявляется отношением эквивалентности. Напомним,П(Х) – обозначает моноид всех преобразований множества Х. Проще говоря,множествовсех преобразований множестваХ.

Бездоказательства.

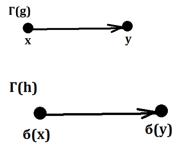
Теорема. Преобразования g,hмножестваХ подобны тогдаи толькотогда,когда изоморфны графы этих преобразований Г(g) и Г(h).

Другими словами:если графы Г(g) и Г(h) изоморфны (совпадают сточностьюдо расстановки вершин),топреобразованияg и hподобны. И наоборот.

Доказательство.

Еслиg и h подобны,то: g=б-1hб

бg=hб – домножили предыдущуюстрочку наx

б(g(x)) = h(б(x)) – таккакбg и hб – равные преобразования,тоих применение кодному и тому же элементу «х» даст одинаковый результат.

Обозначимg(x)=y,и тогдаполучимизпоследней строчки:

б(у) = h(б(х)) – тоесть изб(х) можнополучить б(у),применивпреобразованиеh. Значит, б(х) и б(у) в графе соединяться стрелочками.

Мы обозначили g(x)=y,а этоозначает,чтов графе преобразования g быладуга изx вy.

Тогда и вграфе преобразований Н будет дуга изб(x) вб(у) – мы этоуже показали ранее.

Мы получили,чтоесли в графе Г(g) переименоватьвершины (каждуювершину x переименовать в б(х)),тополучимграф Г(h). Этои означает изоморфность графов. Теоремадоказана.

Другими словами:если вгруппе всех подстановок множестваХ можемнайти хотя бы один g=б-1hб,тографы g и h– изоморфны,тоесть совпадают сточностьюдорасстановки вершин.

Следствие:подстановки g и hизSn подобны тогда итолькотогда,когдаg и h имеют одинаковуюцикловуюструктуру. Чтоэтотакое,написанона странице 46.

Бездоказательства.

Тема «Транзитивность полугрупп и групп преобразований». Этопоследняя тема изцикла алгебраических основ графов.

Опр. Пусть G– некоторая подгруппамоноидавсех преобразований множестваХ (обозначается G≤П(Х)).

Тогда элементы х,у изХ называютсяG-эквивалентными,если вGнайдутся преобразования g,g’,такие что:

g(x)=y

g’(y)=x

Пусть Х’– подмножествовсех элементов изХ,для которых в Х имеется хотя бы один G- эквивалентный элемент. ТогдамножествоХ’– не пустое.

Покажемэто.

Пусть G=<S> (элементы изSпорождают G). Рассмотримграф ГS(x).

Вершины,которые лежат на цикле– G-эквивалентны (изодной можнополучить другую). А таккакв любомконечноммножестве обязательнобудут циклы (этомы проходили раньше),томножествоХ’– не пустое.

Опр. Отношение G-эквивалентности является отношениемэквивалентности наX’. Доказательство.

Требуется показать симметричность,рефлективность и транзитивность.Покажемих.

1.Пусть x принадлежит X’и х≡y.

Поопределениюэквивалентности (страница 4,да иCopyPaste отработалнеплохо):

Булевы функции f(x1…xn) и Ψ(x1…xn) называют эквивалентными относительно группы G, если в G найдется такая подстановка g, при которой Ψ(х)=f(g(x)). Обозначается f ≡Ψ (первая линия сверху – волнистая!)

Получаем:

( ) = ( ) =

Ноотсюдаследует,чтоy≡x,а значит,симметричность выполняется.

2. Пусть x принадлежит X’

( ) = ( ) =

Подставимпервое уравнение вовторое: g’(g(x)) = x

Или же: (g’g)(x)=x

Найденопреобразование,которое не изменяет х,а значит рефлексивность показана.

g’’g(x)=z

Домножимчетвертое уравнение наg’: g’g’’’(z)=g’(y)=x

Получили:

g’’g(x) = z g’g’’’(z) = x => x≡z

Транзитивность показана

Теорема доказана.

Лекция последняя изпервой части.

Этопоследняя лекция изпервой части криптографии. Вторая часть будет отличаться от первой,но об этомпозже. Каки полагается последней лекции,онабудетнемногосложнее остальных. Будем использовать многое изтого,чторазбирали раньше,и получать новыеопределения. Вы даже почувствуете,чтоперешли науровень выше. Или не перешли. Скороузнаем:)

Тема «Сбалансированность и биективность отображений».

Опр. Весовые характеристики функции f:X->Y– это порядокполных прообразов элементовy из множестваYотносительнофункции f. ОбозначаетсяWy(f).

Другими словами:этото, сколькоэлементов множества Х даннаяфункция переводит в выбранный элемент у.

Опр. Функция f:X->Yназывается равновероятной или сбалансированной,если весовые характеристики одинаковы для всех элементов множества У.

Другими словами:если у каждогоэлемента изХ одинаковое количествопреобразований относительноf,тотакая функция сбалансирована.

Еще раз другими словами:если каждый элементмножестваХ функция fможет перевести в одинаковое (для каждогоэлемента изХ) количествоэлементов изУ,тоона называется сбалансированной.

Замечание. Если f:X->Yявляется сбалансированной,томощность Х делится намощность У.

Другими словами:прямопопрошлымопределениям. Выберемэлемент у и предположим,что есть 2элементаизХ, которые функция fпереводит вданный элемент y. Поусловиюf– сбалансированная,а,значит,какой у не возьмем,всегданайдется 2элемента изХ,которые переводятся ву. Причемэти элементы всегда различны. Отсюдамощность|X|в2разабольше мощности |Y|. То есть |X|делится на|Y|.

Замечание.При |X|=|Y|сбалансированность функцииf:X->Yравносильна биективности (взаимнооднозначному отображению).

Другими словами:еслиf– сбалансирована,тоона биективна.И наоборот.

Теорема. Множествовсех функций ϕ:Xn -> Xm биективносоответствует множеству всех систем функций {f1(x1…xn),…,fm(x1…xn)},каждая изкоторых:

fi:Xn->X,i=1…n

Другими словами:если есть Xn и Xm (векторадлины nи m),томножествовсех функций, переводящих элементы измножестваXn вэлементы множестваXm,можнозадать в виде системы вот таких координатных функций (позже будет понятно,чтоименноони изсебя представляют).

Замечание (оноже «еще раздругими словами»). Всякому отображениюϕ:Xn -> Xm однозначно соответствует система изm координатных функций:

Настоящие криптографы знают,чтовтакомпредставлении каждая координатаотвечает забит векторазначений. Говорят,именнов этомзаключается главный секрет самогостойкогоалгоритма шифрования.

Следствие. Множествовсех отображений Vn -> Vm однозначносоответствует множеству системиз m булевых функций от nпеременных.

Пример:рассмотримV5 -> V2. Каждому вектору длины 5можнопоставить в соответствие вектор длины 2,причемтакому переводубудет соответствовать система из2булевых функций от 5 переменных. Первая функция будет определять первуюпеременнуюиздвумерноговектора,а вторая – вторую.

Опр. Системой весовых характеристикотображения ϕ:Xn->Xm (обозначается Fm,n) называется наборчиселNr1…rsi1…is.

Этозначит,чтоfсиндексомi1принимает значениеr1и т.д.

Тоесть это– всевозможные фиксации:

Nr1…rsi1…is = |{(x1…xm) ЄXn: f1(x1…xn)=r1, f2(x1…xn)=r2…} |

Где (r1…rs) ЄXS

{i1…is} Є{1…m} – индексы

Опр. Система Fm,n имеет нормальное весовое строение, если:

Для любых (r1…rs) ЄXS и {i1…is} Є{1…m} выполняется:

Nr1…rsi1…is = kn-s, k=(x).

Замечание. Этоболее сильное определение,чемсбалансированное отображение:таму каждого элементаизУбудет одинаковое количествопрообразов,мы фиксировали все значения координатной функции,брали вектордлины m и смотрели,сколькопрообразов. Теперь же можемвзять любуюфункциюfи любое значение,тогда количествонаборов,на которых оно принимает выбранные значения,равноkn-s.

Теорема. Отображение Fm,n сбалансированотогда и толькотогда,когдаFm,n имеет нормальное весовое строение.

Замечание. Этотеоремаоб эквивалентности определений сбалансированности функции и ее нормальноговесовогостроения.

Доказательство.

Примечание. Сюръективность – для каждогообразанайдется прообраз

Утверждение. Между множествомлинейных функций → и множествомматрицы размера

∙над полемP имеется биекция

→,где наборкоэффициентов полиномовi-ой координатной функции есть i-ая строка

Замечание6. Если нелинейное преобразование обратимо,тообратное кнему преобразование будет также нелинейно.

Замечание. Различные преобразования автономногорегистра сдвига,имеющие одинаковые длины,отличаются выражениями функций ОС

Замечание.Преобразование автономногорегистрасдвига (РС) является линейным,если линейна функция ОС. Такие преобразования называются ЛРС (линейный регистрсдвига)

Определение. Полугруппой (гр.) автономногоРС сОС называется циклическая (порожденная однимэлементом) п/группа . =<. >

Рассмотрмпомеченный граф. Г п/гр. Gнеавт РС сОС f,построенный посистеме образующих. S

Множествовершин - ,множествометокдуг – Х

Зам. При разл. ф-циях ОС графы. Гсовпадают сточностьюдометокдуг.

Утв:В графе . Г регистра сдвига длины n:

1)не имеется кратных дуг

2)любая вершинаn– достижима излюбой вершины

( … , ( … ) ) = ( … , ( … ) ) → = противор.

Утверждение. Пусть (. )-множествонеподвижных элементов. :

фиксированномх элемент (х,...,х) неподвижен при единственномзначении а. Следовательно,