
Разбор лекций
.pdf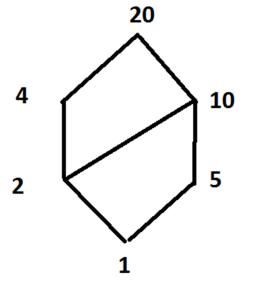
Тема «Полурешетки, решетки и подрешетки»
Эта тема основана на предыдущей, это будет понятно уже с первых определений. Здесь снова почти не будет теорем, зато определений – еще больше.
Опр. Пусть У – подмножество ч.у.м. Х и х Х. Элемент хназываетсянижней (верхней) границей множества У, если x≤y (y≤x) для всех y Y.
Другими словами: элемент х является нижней границей множества У, если он меньше (или равен) любого элемента из У. С верхней границей аналогично.
Опр. Нижняя (верхняя) граница х множества У называется его нижней (верхней) гранью, если z≤x (x≤z) для любой нижней (верхней) границы z множества У. Обозначается x=inf(Y) (x=sup(Y)).
Другими словами: нижняя грань – это максимальная нижняя граница.
В приведенном ниже графе для (4,10,20) нижней гранью является 2 (максимальное число, которое меньше 4, 10 и 20)
Дополнительные обозначения:
Inf(x,y)=x y
Sup(x,y)=x y
Из определений верхней и нижней граней:x≤yx y=x x y=y
Опр. Ч.у.м. Хназывается нижнейполурешеткой, если x y Хдлявсех х,у Х.
Опр. Ч.у.м. Хназывается верхней полурешеткой, если x y Хдлявсех х,у Х.
Другимисловами: нижняя/верхняя граньлюбых ч,у из Хтакженаходится в Х
Опр. Ч.у.м.называетсярешеткой, если Хявляетсяинижней, иверхней полурешеткой.

Другимисловами: нижняяи верхняягранидлялюбых х,у их Хтакженаходятсяв Х.
Замечание. В верхней (нижней) полурешеткеХэлементsup(X) (inf(X)) определен однозначно.
Пустьэтонетак:есть2 разныеверхниеграни Х:
x≠y
x=sup(X)
y=sup(X)
Поопределениюверхней грани:x≤y, y≤x. НоХ – ч.у.м, авнем антисимметричность (если x≤y & y≤x,тоx=y) выполняется. Отсюдах=у.
Опр. Внижней (верхней) полурешеткеХимеетсянуль,т.е. наименьший (единица, т.е. наибольший) элемент. Обозначается0Х и 1Х.
Другимисловами: 0Х –минимальныйэлемент,1Х –максимальный.
Опр. Атомом нижней (коатомом верхней) полурешетки Хназывают всякийэлементх со свойством x>-0X (1X>-x).
Другимисловами: напомним, чтоy>-x означает, что между x<yнельзявставитьникакой элемент. Тоестьатом–элемент, следующий сразу заминимальным (обозначаетсянулем), коатом –элемент,следующий сразу замаксимальным (обозначаетсяединицей).
Ещераз другими словами: награфениже0X=000; 1Y=111, и ничегонельзявставитьмежду:
000и 001
000и 010
000и 100
111и 011
111и 101
111и 110
Следовательно,001, 010, 100– атомы, а011, 101и110– коатомы.
Замечание. В нижней (верхней) полурешеткеХпорядкабольше1, каждый отличный от 0X и 1X элемент или совпадает,или сравнимхотя бы содним изатомов(коатомов) решетки.

Опр. Гомоморфизмf:X->Yдляполурешеток и решеток Хи Уможноопределитьчетырьмя способами. Ивсеправильные.
1.F – изотонная функция ч.у.м. Напомним:
Опр. Пусть имеется ч.у.м <X, ≤ > и к.у.м. <У,  >. Функция f:X->Y называется сохраняющей порядок (изотонной или гомоморфизмом ч.у.м), если для любых
>. Функция f:X->Y называется сохраняющей порядок (изотонной или гомоморфизмом ч.у.м), если для любых
x,x’ |
Х сосвойством |
x≤x’ выполнено f(x) f(x’). |
|
Другими словами: имеем чум Х и кум У. Функция f принимает на вход элемент из Х и возвращает элемент из У. Эта функция называется гомоморфизмом, если для
любых x,x’ Х сосвойством x≤x’ выполнено f(x) f(x’). Напомним, знак
f(x’). Напомним, знак  означает выполнение рефлексивности (x≤x) и транзитивности (если х≤у, у≤z, то х≤z). То есть меньшие элементы множества Х переводятся в меньшие элементы множества У).
означает выполнение рефлексивности (x≤x) и транзитивности (если х≤у, у≤z, то х≤z). То есть меньшие элементы множества Х переводятся в меньшие элементы множества У).
2.F(x y)=f(x) f(y) для любых x,y Х.
Читается:нижний гомоморфизмили гомоморфизм нижних полурешеток
3.F(x y)=f(x) f(y) для любых x,y Х.
Читается:верхний гомоморфизмилигомоморфизм верхних полурешеток
4.F – и верхний, и нижний гомоморфизм.
Читается: решеточный гомоморфизм или гомоморфизм решеток.
Опр.Биективныйгомоморфизм решеток (условия:п.4изпредыдущегоопределения+f- биективна)называетсяизоморфизмом решеток.
Опр.Еслиf:X->Y–гомоморфизмрешеток илинижнихполурешеток,тополныйпрообраз элемента0Y называетсяядром гомоморфизмаf (обозначаетсяKer(f)).
Чтотакоеполныйпрообраз?А вот что:еслизаданоотображениеF:X->Y,y Y,то множество{x X|F(x)=y} X называетсяполнымпрообразом элементаy.В принципе, такие обозначенияуженужночитатьбез проблем:если заданафункция, принимающаянавход элементыиз Х ивозвращающая элемент изУ, томножество таких х, чтоF(x)=y, называется ядром. Естественно, увзятизмножестваУ. Внашем случаенаегоместестоит 0У.
Опр. Нижняя(верхняя) полурешеткаУназываетсяподполурешеткойнижней (верхней) полурешетки Х, если У Х иinf(x,y) (sup(x,y)) в полурешеткеУсовпадает сограничением функции inf(x,y):X2->X(sup(x,y):X2->X) намножествоY2.
Другимисловами: здесь говоритсяпро2 условия–У входитв Х,и нижняяграньполурешетки У совпадает сограничением функции inf(x,y):X2->XнамножествоY2. Незнаю,чтотакое ограничениефункции intнамножество У2, нонапрактикеэтообычноозначает, что inf полурешетки Х совпадаетсinf еенижних подполурешеток.
Опр. РешеткаУназываетсяподрешеткой решеткиХ, если Уявляетсяи нижней,и верхней подполурешеткой решетки Х.
Другимисловами: еслиподполурешеткаявляетсяи нижней, иверхней, тоонаполучает право называтьсяподрешеткой.
Утверждение. Пусть У1…Ук –нижние(верхние) подполурешетки нижней(верхней) полурешетки Х. Тогда< , ≤ >- нижняя(верхняя) подполурешеткаполурешетки Х.
Другимисловами: пересечениянижних/верхнихподполурешеток есть нижние/верхние подполурешетки.
Доказательство.
Обозначим У =< , ≤ >.По условию Yi –нижняяполурешетка, поэтомуinf(x,y)€Yi при любых x,y€Yi,i=1..k. Этопоопределению нижней полурешетки. Следовательно, inf(x,y) €Y при любых x,y. ОтсюдаподмножествоУнижней полурешетки Хявляетсянижнейполурешеткой (то жеопределение, нов обратную сторону).
ПоусловиюУi –нижниеподполурешеткиполурешетки Х,поэтому inf(x,y) в полурешеткеХ совпадает сinf(x,y) в полурешеткеУi длявсех x,y€Yi и, следовательно, совпадает сinf(x,y) в полурешеткеУдлявсех х,у. Значит, У–нижняяподполурешеткаполурешеткиХ.
*Первый шаг(Поусловию Уi –нижниеподполурешетки полурешетки Х,поэтому inf(x,y) в полурешеткеХ совпадает сinf(x,y) в полурешеткеУi длявсех x,y€Yi)получен изопределения нижней полурешетки.
Второй шаг (и,следовательно, совпадаетсinf(x,y)в полурешеткеУдлявсех х,у.)– логически (если inf у всех Yi одинаковый,тоон ив пересечениепопадает, ив этомпересечении продолжит оставаться inf).
Третий шаг –определениенижнейполурешеткивобратную сторону.
Опр. Прямымпроизведением ч.у.м <X, > и ч.у.м.<Y,
> и ч.у.м.<Y, > называетсяч.у.м.<XxY,≤ >,гдедля любых x,x’€Xи y,y’€Yвыполняется:
> называетсяч.у.м.<XxY,≤ >,гдедля любых x,x’€Xи y,y’€Yвыполняется:
(x,y)≤(x’, y’) x x’ и y
x’ и y y.
y.
Другимисловами:длялюбых парх,уи х’,y’,таких что(x,y)≤(x’, y’),выполняютсясвойстваx x’ и y
x’ и y y.
y.
Чтотакоетреугольник содним идвумя знаками сверху? Честнохотел найти ответнаэтот вопрос. Перелистал первыепараграфы, но все, чтоувидел– этотреугольникснижним подчеркиванием (ужерассматривали ранее– этоквазиупорядоченныемножества, т.е. выполняются отношениярефлексивности (x≤x)итранзитивности(если x≤yи y≤z,то x≤z)). Ничегопротреугольникисверхнимподчеркиванием нет.Поэтомунормальноразобратьэту теорему неполучится. Доказательство разобрал по большейчасти интуитивно, совсемне уверен, чтоправильно.Поэтомуегоможнопропустить.
Доказательство.
Пусть:
x, x’ €X
a=x x’

y, y’€ Y
b=y y’
Т.к. Х иУпоусловиюполурешетки,то, поопределению, получимa€X, b€Y.Значит, (a,b)€ XxYи (a,b) – нижняяграницапары ((x,y),(x’,y’)). Почему?Посмотритенаначалодоказательства, сразу послеслова«Пусть».Длянадежностиможновспомнить определениенижней границыx: x≤y для любых y изY.
Мы узнали, что(a,b) –нижняяграница. Аграньлиэто?Ведь нижняягрань– этомаксимальная из нижнихграниц. Теперь вспомним определение,котороенаписанопрямонадтеоремой. Вот
оно: (x,y)≤(x’, y’) x x’ и y
x’ и y y. Возьмемлюбуюдругую нижнююграницу (a’, b’). Всилу
y. Возьмемлюбуюдругую нижнююграницу (a’, b’). Всилу
определенияэлементов aи b онаудовлетворяет неравенствам: a’ aи b’
aи b’ b. Почему? Немогу сказать, потому чтонеизвестно, чтотакоетреугольниксверхнимподчеркиванием.Воттакиз-за отсутствияинформацииоб этомстановитсябесполезнымвседоказательствотеоремы:(
b. Почему? Немогу сказать, потому чтонеизвестно, чтотакоетреугольниксверхнимподчеркиванием.Воттакиз-за отсутствияинформацииоб этомстановитсябесполезнымвседоказательствотеоремы:(
Если невникать, почему, апростопринять, чтоa’ aи b’
aи b’ b, получаем, что(a’,b’)≤(a,b) – из чуть ранееупомянутогоопределения.Следовательно, (a,b) – нижняяграньпары ((x,y),(x’,y’)). Отсюда<XxY,≤>- нижняяполурешетка. Напомним, нижняяполурешеткаозначает выполнение условияx y€Xдлявсех x,y€X.Мыэтоидоказали:взяли по2элемента(х,х’и y,y') из Хи У,нашли дляних нижниеграни, определилинижнююграньдляпары ((x,y),(x’,y’)).В свою очередь, (a,b)€Х. Получаем, чтодляпарыэлементов найденанижняягрань,и онапринадлежитХ. Следовательно,<XxY, ≤> -нижняяполурешетка.
b, получаем, что(a’,b’)≤(a,b) – из чуть ранееупомянутогоопределения.Следовательно, (a,b) – нижняяграньпары ((x,y),(x’,y’)). Отсюда<XxY,≤>- нижняяполурешетка. Напомним, нижняяполурешеткаозначает выполнение условияx y€Xдлявсех x,y€X.Мыэтоидоказали:взяли по2элемента(х,х’и y,y') из Хи У,нашли дляних нижниеграни, определилинижнююграньдляпары ((x,y),(x’,y’)).В свою очередь, (a,b)€Х. Получаем, чтодляпарыэлементов найденанижняягрань,и онапринадлежитХ. Следовательно,<XxY, ≤> -нижняяполурешетка.
Опр.Пусть У Х,гдеХ–нижняя(верхняя)полурешетка.Нижней(верхней) подполурешеткой,порожденноймножеством У (обозначается<[Y],≤>)называется минимальнаянижняя(верхняя)подполурешеткаполурешеткиХ,содержащаямножествоУ. Полурешетка[Y} содержитсявовсякойнижней(верхней)подполурешетке,содержащейУ.
Другимисловами:нарисуем граф инайдем нижнююполурешетку,порожденную множеством{4,5,6}
Начнемсначала.Нижнейподполурешеткой,порожденноймножеством{4,5,6},называется минимальнаянижняяподполурешеткаполурешеткиХ,содержащаямножество{4,5,6}.
Нижняяподполурешеткаот настребует включить вседонижнейгранизаданногонабора элементов.Визуальноэтоточка,изкоторойестьпуть долюбогоизэлементов{4,5,6}. В

нашемслучаеэтоточка0.Поэтомунижняяподполурешетка,порожденнаямножеством {4,5,6},будет включать всеэлементы,кроме7.
Еслибыискалидляэлементов{5,6},тобылобы достаточнодобавить «3».
Опр.Идеалом решетки(иливерхнейполурешетки)Хназывается еенепустое наследственноеподмножествоУ,замкнутоеотносительнооперации .
Другимисловами:строимграф иразбираемся.Граф пустьбудеттакойже:
Построим идеал дляэлементов{5,6}.
1.Должнасоблюдатьсязамкнутость относительно .Тоесть длякаждых2элементов долженнайтись максимум(верхняягрань,точнее).Для 5и6этосемерка. Добавляем еек нашемуидеалу.
2.Должнасоблюдатьсянаследственность (нужновключить все,чтоменьшезаданных элементов).Включаем элементы3,0,2,т.к. онименьшеи5,и 6.
Полученидеал –0,2,3,5,6,7
Утв.Еслиf –гомоморфизмверхнейполурешеткиХнаверхнююполурешеткуУ снулем,то множествоKer(f)являетсяидеаломвХ.
Доказательство.
Пусть f(x’)=0Y их≤х’.
Тогдаx x’=x’иf(x x’)=f(x’)=0Y.– соднойстороны,f(x x’) =0Y.
Вместестемf(x x’)=f(x) f(x’)=f(x) 0Y=f(x). –сдругойстороны,f(x x’)=f(x).
Значит,f(x)=0Y иKer(f)–наследственноеподмножествоХ.Напомним, чтоKer(f)–это полныйпрообразэлемента0У,т.е.набор всехх,такихчтоf(x)=0Y.Внашемслучаех≤х’и f(x)=f(x’)=0.Отсюданаследственность.
Осталось узнать,замкнутолиKer(f)относительно ,т.к.этотребует идеал.
F(x)=f(x’)=0Y,тогдаf(x x’)=f(x) f(x’)=0Y.Значит,x x’€Ker(f)=> этоидеал.
Напомним,f(x x’)=f(x) f(x’)–определениегомоморфизмаверхнейполурешетки.

Тема«Алгебрарешетки,дистрибутивныерешетки»
ДлярешеткиХфункции и определенынаХ2 ипринимают значениявХ,т.е.являются бинарнымиоперацияминаХ.Другимисловами,Х2означает, чтонавход принимаетсядва элемента,аХозначает, чторезультатомявляется1элемент.
Длялюбыхx,y,z€Xвыполняютсяследующиесвойства:
1.Идемпотентность: x x=x;
x x=x
2.Коммутативность: x y=y x; x y=y x
3.Ассоциативность: x (y z)=(x y) z; x (y z)=(x y) z
4.Поглощение: x (y x)=x (y x)=x
5.Совместимость:
x≤y x y=x x y=y
Сообщается,чтолюбаяалгебраХсдвумябинарнымиоперациями, удовлетворяющим 1-4, являетсярешеткой,иобратно.
Замечание.
Влюбойрешеткеравносильнытождества:x,y,z€X:
x (y z)=(x y) (x z)
x (y z)=(x y) (x z)
Есливыполненыобатождества,торешеткаХназываетсядистрибутивной.
Пример дистрибутивнойрешетки:
Действительно,какиебы3элементаневзяли,всегдатождествавыполнены.
Например,x=1,y=2,z=3:

Пример недистрибутивнойрешетки:
Возьмем так же:х=1,y=2,z=3:
1 (2 3)=(1 2) (1 3)
ВАЖНО!ДОДЕЛАТЬ!!!!!!!!!!!!!!!!!!!!!!!!!
Опр.Элемент хрешеткиХ,гдех≠0Х,называется -неразложимым,еслиизx=y z следует,
чтоx=yилиx=z.
Элемент хрешеткиХ,гдех≠1Х,называется -неразложимым,еслиизx=y z следует,что x=yилиx=z.
Другимисловами:ВАЖНО!ДОДЕЛАТЬ!!!
Опр.Пусть Х–решетка,x,y,z Х. Максимальныйэлемент усосвойствомx y≤zназывается относительным -псевдодополнениемх вz.
Опр. Минимальный элемент у сосвойством x y≤zназываетсяотносительным -
псевдодополнением хвz.
Опр.Пусть Х–решетка,x,y,z Х. Максимальныйэлемент усосвойствомx y =0Х называется - псевдодополнением х.
Опр. Минимальный элемент у сосвойством x y=1Х называется -псевдодополнением х.
Другимисловами:атут исказать нечего.Ищемэлементыстакимисвойствами,давыбираем максимальный.Толькообратитевнимание:первыедваопределения– относительные (имеетсяэлемент z),аследующаяпара–общие длявсейрешетки.
Утв.ВконечнойдистрибутивнойрешеткеХдлялюбыхэлементовхиz верхниеинижние псевдодополненияопределены однозначно.
Доказательство.Доказывать будем методомот противного:пусть существуют yиy’– различныенижниепсевдодополненияхвz.Они несравнимы,иначеодинихнихнебыл бы максимальным (нудействительно,поопределениюпсевдодополненийэлементыдолжны быть максимальными,удовлетворяющиезаданным условиям).По определениюнижнего псевдодополненияимеем:

x y≤z
x y’≤z
Значит,z –верхняяграницадляэлементовx yиx y’.(по определению:верхняяграница– этоэлемент х,такойчтоx≥yдлявсехyизмножестваУ,внашемслучае множествоУ–этоx
yиx y’).
Поэтомуверхняягрань этихэлементовнепревосходитz:
(x y) (x y’)≤z.
(этоопять поопределению:верхняягрань–этотакаяверхняяграницаx,чтоx≥z длялюбой верхнейграницыz измножестваУ.Дапо сутиz иесть верхняягрань –верхняяграницадвух элементов).
Зачемнам этот шаг?Чтобыиспользовать свойстводистрибутивности(x (y z)=(x y) (x z))ипреобразовать
(x y) (x y’)≤z
К виду:
x (y y’)≤z
Чтоэтодает?А вот что!Посмотритенато,чтополучилось.И нато,чтописалось чуть ранее. Янапишуэтовстолбик,чтобывынисекундуне сомневались:
x (y y’)≤z
x y≤z
x y’≤z
И мыоказались водномшагеот финала.Осталось вспомнить,чтоyиy’несравнимы(это отметилиранее),поэтомуихверхняяграницазаведомобольшелюбогоизних: y y’>yиyy’>y’.Нуправда,любогографадостаточно,чтобыэтопоказать.Дажекусочкаграфа.Вот вамнесравнимыеэлементы01 и10 иихверхняя грань 11:
Сложимвсевкучу.Поусловиюyиy’–нижниепсевдодополнения.По определениюэто значит,чтоони–максимальныеэлементысосвойствомx y≤z. Ачтоунасполучилось?
Авот что: x (y y’)≤z
Из этогоследует,чтоестьэлемент,больший yи y’,всестем жесвойством.

Противоречие. Предположениеосуществовании yи y’ неверно. Единственностьдоказана. Трава зеленая. Небоголубое. Котятадовольны.Птички…
Тема«Решеткадвоичныхn-мерныхвекторов»
Этатемаотличаетсяотдругих. Нет,здесьтежеопределения, утвержденияит.д. Ноесть одна лемма.ЛеммаАнселя. Несамаяприятнаявещь,ноделоопять нев этом.Делов ее доказательстве, котороеогромно, какдисксвиндой. Разбореедоказательстваможносравнитьс разбором назначения каждогофайлав system32.Ктоневтеме–там более100,000файлов. Поэтому еедоказательствомы пропустим. Это происходитпокачто первыйраз и, обещаю,таких случаев будетминимальноеколичество.
Опр. Весдвоичноговектора– эточислоегоединичных координат.
Другимисловами: знакомоеопределениеизпрошлого семестра. Дажедобавитьнечего. Считаем количествоединиц встолбцезначенийтаблицы истинности,этомуи равен вес. В приведенной таблицевесравен 3
Опр. Расстоянием Хэммингамеждувекторамиα,β Vn называетсячислонесовпадающих соответственныхкоординатэтих векторов. Обозначаетсяdist(α,β).
Другимисловами: по-моемутожепонятно. Нудавайтепример. В немdist(a,b)=2.
Опр. Векторaменьшеилиравен вектору b, если они меньшеилиравны покоординатно.Для любителейформул: α≤β αi≤βi для i=1…n.
Утв. ПустьХ естьn-множество. Тогда<2X, >-дистрибутивнаярешеткаи<2X, >≡<Vn, ≤>.
Другимисловами: напишуэто утверждениебез непонятных символов.Пусть Х–множествос количествомэлементовn.Тогдачастично-упорядоченноемножество2Х по поношению являетсядистрибутивной решеткой(решеткой, гдеравносильнытождества:x (y z)=(x y)
(x z)иx (y z)=(x y) (x z)),ич.у.м.<2X, > эквивалентнаотносительно ч.у.м. <Vn,≤>
Напомним,ч.у.м.<2X, > -этотам,гдевыполняются:
1.Рефлексивность (x x)
2.Антисимметричность (если x y &y x,тоx=y)
