1.4. Точность оценивания параметров

Допустим теперь, что при оценивании параметров научились строить такие функции , которые дают несмещенные и состоятельные оценки параметров . В этом случае за характеристику точности оценок естественно выбрать их дисперсию , т.е. меру разброса вокруг значения . В математической статистике показано, что лучше всего за меру точности несмещенных оценок выбрать вес оценки, т.е. величину:

. (1.5)

Встает вопрос, как точно можно оценивать параметры _i при заданном объеме выборки n. Другими словами, как сильно можно уменьшить дисперсию (увеличить вес) оценки при заданном n? Ответ на этот вопрос дали Крамер и Рао независимо друг от друга.

Сначала рассмотрим случай оценивания одного параметра. Пусть функция правдоподобия выборки зависит от одного параметра, так что она имеет вид , и пусть имеется статистика несмещенная оценка параметра . Крамер и Рао показали, что в этом случае:

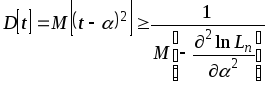, (1.6)

где:

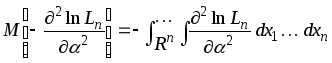. (1.7)

Величина (1.7) при условии сходимости интеграла называется информационным количеством Фишера. Эта величина не зависит от способа оценивания , т.е. от статистики и представляет собой нижнюю границу точности любой оценки. Другими словами, при заданном объеме выборки точность несмещенной оценки параметра  будет ограничена снизу.

В случае повторной выборки:

и ,

Тогда из (1.6), (1.7) легко подсчитать:

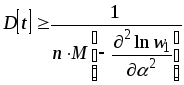, (1.8)

а вес оценки

.

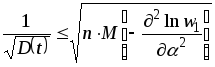В весьма широком классе несмещенных оценок вес оценки при повторной выборке не может быть больше величины, пропорциональной квадратному корню из числа наблюдений. Оценка t_e, для которой в неравенствах (1.6), (1.8) достигается знак равенства, называется эффективной.

Пример. Возвращаясь к примеру оценки параметра  нормального распределения, получаем:

.

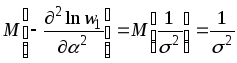Откуда

. (1.9)

Для выборочного среднего получается:

. (1.10)

Т.е. оценкаимеет максимально возможную точность и является эффективной.

В случае оценивания нескольких параметров функция правдоподобия имеет вид (1.1). Пусть статистики

(1.11)

являются несмещенными оценками соответствующих параметров.

Составим матрицу

, где 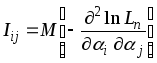. (1.12)

Матрица I называется информационной матрицей Фишера. А квадратичная форма является положительно полуопределенной. Будем считать, что ,где . Тогда

(1.13)

является корреляционным эллипсоидом случайного вектора

. (1.14)

Теперь рассмотрим набор несмещенных оценок (1.11) и составим вектор случайных уклонений с нулевым вектором средних и корреляционной матрицей

. (1.15)

Если сформировать теперь квадратичную форму при любом векторе , то имеет место следующая теорема.

Теорема Рао-Крамера. При условии существования неособенной информационной матрицы Фишера I (1.12) и величин , при любом имеет место неравенство:

, (1.16)

где B_t – корреляционная матрица (1.15) вектора оценок (1.11).

Если теперь вектор Z такой, что , то из (1.16) следует, что корреляционный эллипсоид охватывает корреляционный эллипсоид . Т.е. с помощью любых статистик t нельзя получить более точных оценок , чем в случае, когда эти два эллипсоида совпадают.

Статистики t_i, дающие несмещенные оценки параметрам _i , для которых эллипсоид совпадает с эллипсоидом , называется совместно эффективными оценками параметров .

11.5. Методы оценивания.

Основными способами оценивания параметров в математической статистике являются: метод максимального правдоподобия и метод моментов. Метод моментов введен К. Пирсоном. Пусть имеется повторная выборка с функцией правдоподобия

Составляет mвыборочных моментов

.

При

,

т.е. с ростом объема выборки оценки m_становятся состоятельными.

Метод максимального правдоподобия разработан Д. Бернулли, Ф. Гауссом и К.Р. Фишером. При этом способе за оценки выбираются такие значения параметров, которые дают максимальное значение функции правдоподобия, если их подставить на место . Если для повторной выборки дифференцируема, то пользуясь однозначностью логарифмической функции, удобнее искать максимум не самой функции правдоподобия, а ее логарифма. В этом случае уравнения правдоподобия примут вид

. (1.17)

Оценки, получаемые из уравнения (1.17) называются оценками максимального правдоподобия. Они обозначаются и имеют ряд замечательных свойств. Данные оценки асимптотически несмещенные, асимптотически эффективные и асимптотически нормальные. Как правило, уравнения (1.17) имеют единственное решение.

Пример. Оценки иs² параметров  и  ² нормального распределения по выборке x_i  являются оценками максимального правдоподобия, т.е. они получены из решения системы (1.17), записанной для функции правдоподобия из рассматриваемых в данной главе примеров.