
- •Вероятностное описание погрешностей измерения
- •1. Случайные события и их вероятности
- •2. Случайные величины и их распределения
- •3. Числовые характеристики случайных величин
- •4. Распределения, часто встречающиеся в задачах метрологии
- •5. Системы случайных величин и их характеристики
- •1. Необходимые сведения из математической статистики.
- •1.1. Выборка. Статистика.
- •1.2. Оценивание параметров
- •1.3. Несмещенные и состоятельные оценки.
- •1.4. Точность оценивания параметров
- •1. Введение
- •2. Обработка результатов прямых измерений
- •2.1. Точечное оценивание
- •2.2. Оценивание с помощью доверительных интервалов
- •2.3. Примеры решения задач Опыты Милликена [1, стр.102].
- •Проверка статистических гипотез
- •1. Проверка гипотезы о равенстве математического ожидания заданному значению
- •2. Проверка гипотезы о равенстве дисперсии заданному значению
- •3. Проверка гипотезы о равенстве двух дисперсий
- •4. Резко выделяющиеся наблюдения
- •5. Примеры решения задач
- •5.1. Проверка гипотез
- •5.2. Опыты Кэвендиша [1, стр.105]
- •Обработка результатов прямых неравноточных измерений
- •1. Точечное оценивание
- •2. Оценивание с помощью доверительных интервалов
- •3. Пример неравноточных измерений
- •Обработка результатов совместных измерений
- •1. Случай линейной системы уравнений
- •2. Случай нелинейной системы уравнений
- •3. Важные частные случаи
- •3.1. Случай равноточных измерений
- •3.2. Линейная регрессия
- •3.3. Полиномиальная регрессия
- •4. Примеры совместных измерений
- •4.1. Исследование зависимости сопротивления проводника от температуры
- •4.2. Исследование зависимости поверхностного натяжения от потенциала электрода
4. Примеры совместных измерений
4.1. Исследование зависимости сопротивления проводника от температуры
С целью установления
зависимости сопротивления медного
проводника от температуры
![]() были проведены совместные измерения
его температуры
были проведены совместные измерения
его температуры![]() и сопротивления
и сопротивления![]() .
Данные приведены в таблице 1. Предполагая,
что априори известен линейный характер
этой зависимости
.
Данные приведены в таблице 1. Предполагая,
что априори известен линейный характер
этой зависимости
![]() ,
,
где
![]() – сопротивление проводника при
температуре
– сопротивление проводника при
температуре![]() ;
;![]() – температурный коэффициент сопротивления,
необходимо из экспериментальных данных
оценить неизвестные коэффициенты
– температурный коэффициент сопротивления,
необходимо из экспериментальных данных
оценить неизвестные коэффициенты![]() и
и![]() .
Температура
.
Температура![]() .
.
Используя заданный
вид зависимости сопротивления медного
проводника от температуры и экспериментальные
данные, составим систему из
![]() уравнений
уравнений
![]()
![]() . (21)
. (21)
Преобразуем систему (21) к виду
![]()
![]() . (22)
. (22)
Введем
обозначения
![]() ;
;![]() ;
;![]() ;
;![]() .
Тогда система (22) примет вид, полностью
совпадающий с (15). Если теперь предположить,
что наблюдаемые значения сопротивления
известны с погрешностями, которые
распределены по нормальному закону с
нулевым математическим ожиданием и
неизвестной, но одинаковой дисперсией
.
Тогда система (22) примет вид, полностью
совпадающий с (15). Если теперь предположить,
что наблюдаемые значения сопротивления
известны с погрешностями, которые
распределены по нормальному закону с
нулевым математическим ожиданием и
неизвестной, но одинаковой дисперсией![]() ,
то систему (22) можно решить по МНК. Оценки
коэффициентов
,
то систему (22) можно решить по МНК. Оценки
коэффициентов![]() и
и![]() будут задаваться выражениями (16) и (17),
где все весовые коэффициенты
будут задаваться выражениями (16) и (17),
где все весовые коэффициенты![]() .
.
|
|
|
|
|
|
|
1 |
19.989 |
20 |
|
0 |
|
2 |
20.083 |
21 |
1 |
1 |
|
3 |
20.172 |
22 |
2 |
4 |
|
4 |
20.235 |
23 |
3 |
9 |
|
5 |
20.319 |
24 |
4 |
16 |
|
6 |
20.412 |
25 |
5 |
25 |
|
7 |
20.475 |
26 |
6 |
36 |
|
8 |
20.555 |
27 |
7 |
49 |
|
9 |
20.647 |
28 |
8 |
64 |
|
10 |
20.713 |
29 |
9 |
81 |
|
11 |
20.808 |
30 |
10 |
100 |
|
12 |
20.869 |
31 |
11 |
121 |
|
13 |
20.962 |
32 |
12 |
144 |
|
14 |
21.033 |
33 |
13 |
169 |
|
15 |
21.112 |
34 |
14 |
196 |
|
16 |
21.205 |
35 |
15 |
225 |
|
17 |
21.283 |
36 |
16 |
256 |
|
18 |
21.365 |
37 |
17 |
289 |
|
19 |
21.446 |
38 |
18 |
324 |
|
20 |
21.524 |
39 |
19 |
361 |
|
21 |
21.585 |
40 |
20 |
400 |
Таблица 1.
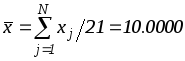 ,
,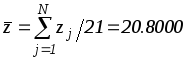 ,
,
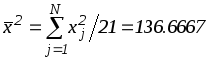 ,
,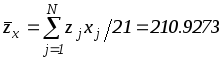 ,
,
![]() ,
,
![]() .
.
Следовательно, зависимость сопротивления медного проводника от температуры в рамках рассматриваемой линейной модели имеет вид
![]() .
.
Найдите самостоятельно
оценку параметра
![]() и дисперсионную матрицу ошибок
коэффициентов
и дисперсионную матрицу ошибок
коэффициентов![]() и
и![]() .
.
