Оценивание характеристик погрешностей
Оценка МО]:
,
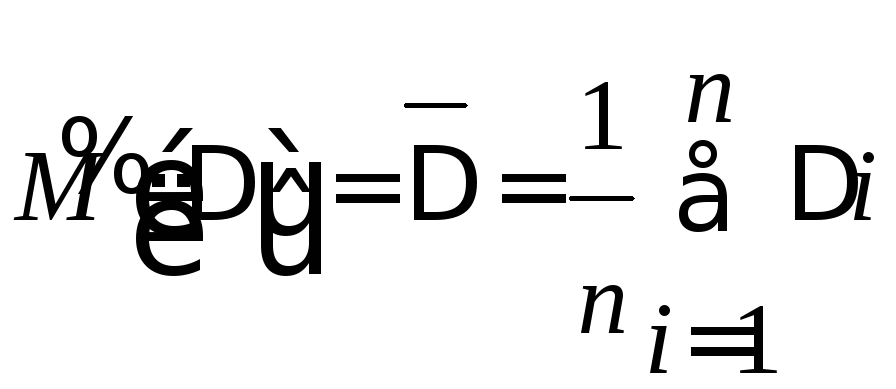n
– число наблюдений.
Оценка СКО:
=
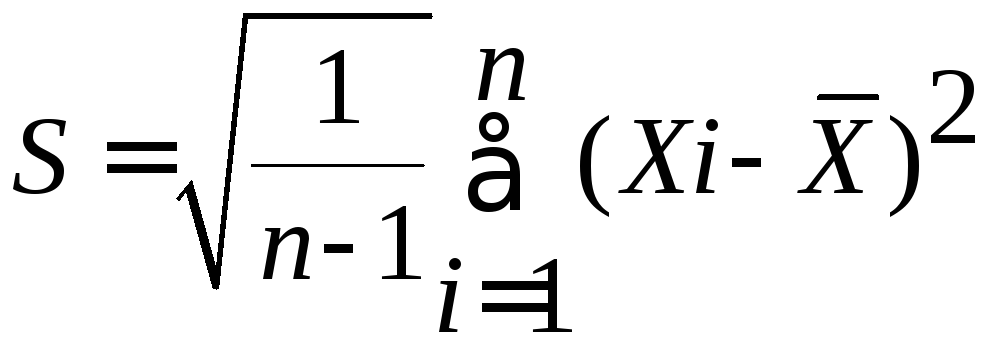
Оценка
СКО среднего арифметического: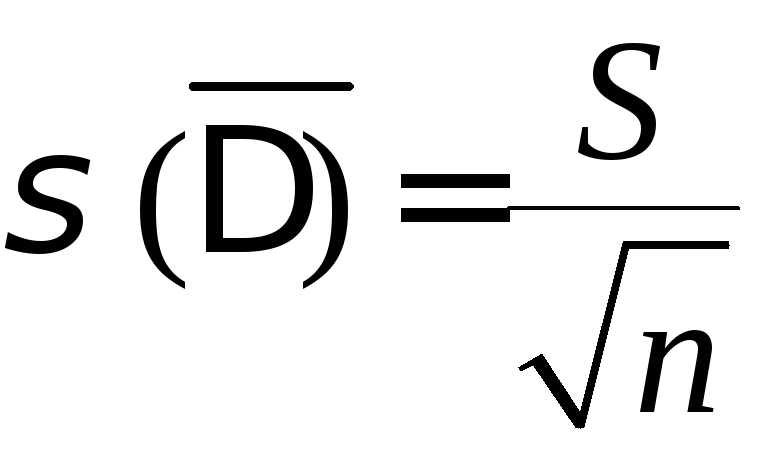 
Истинное
значение 
находится в границах интервала:
=
Рдов
;
-
коэф. Стьюдента
для числа степеней свободы ν
=
n-1
и уровня значимости α
= 1-Р.
Р
+
Границы
доверительного интервала для среднего
значения 
:
;
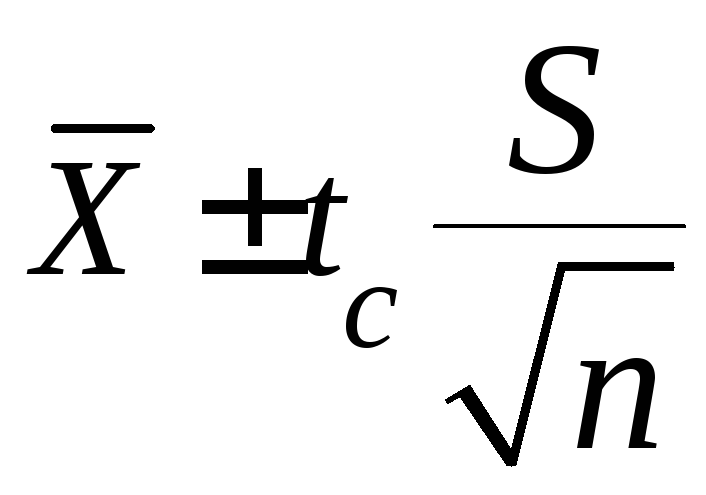Р
Для определении доверительных границ СКО используют χ2 - распределение Пирсона (ν = n -1 α=1-Р):
Р
σн
σв
Если
распределение наблюдений нормально,
то χ2
=
.
;
;
;
;
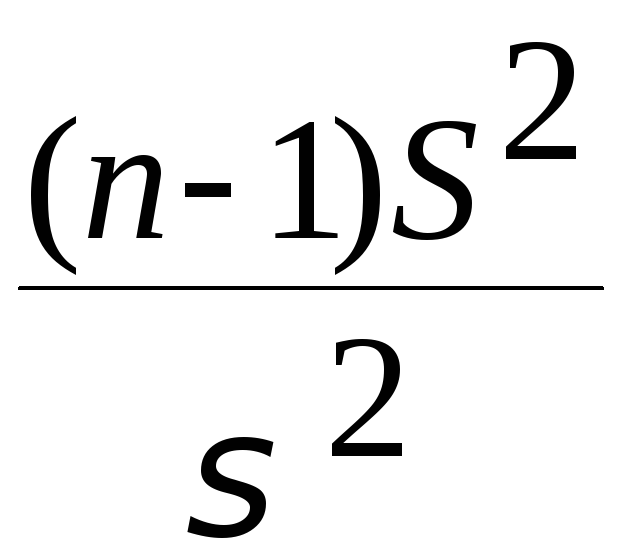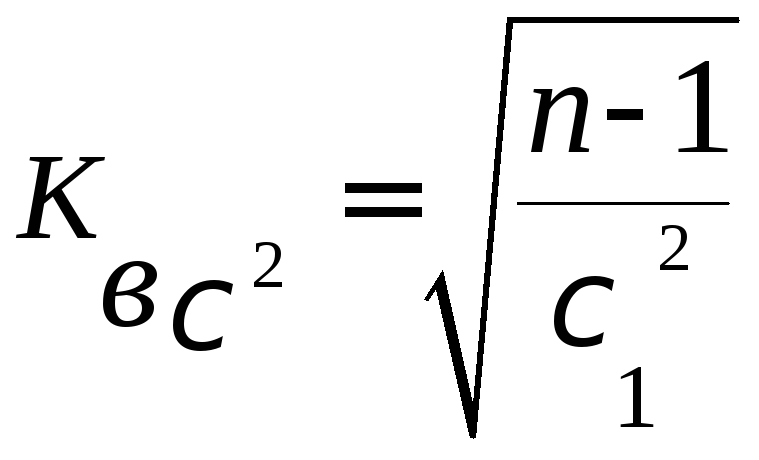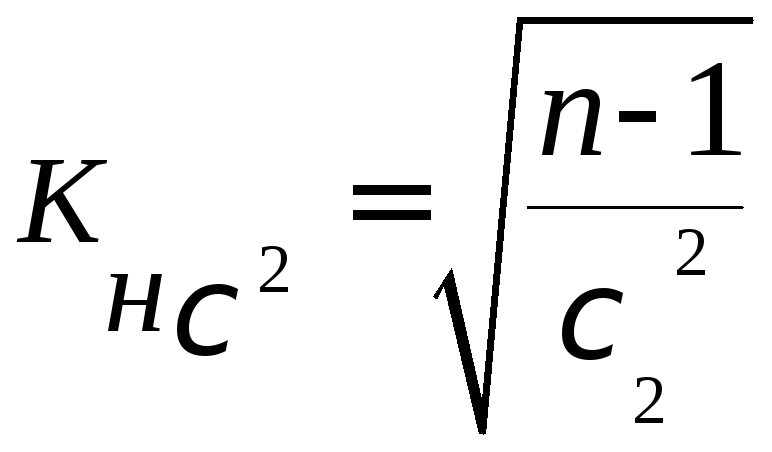находят
для уровня значимости 1-α/2,
-
для
α/2,
где
α=1-Р.
Приближенная
оценка:
=
;
(
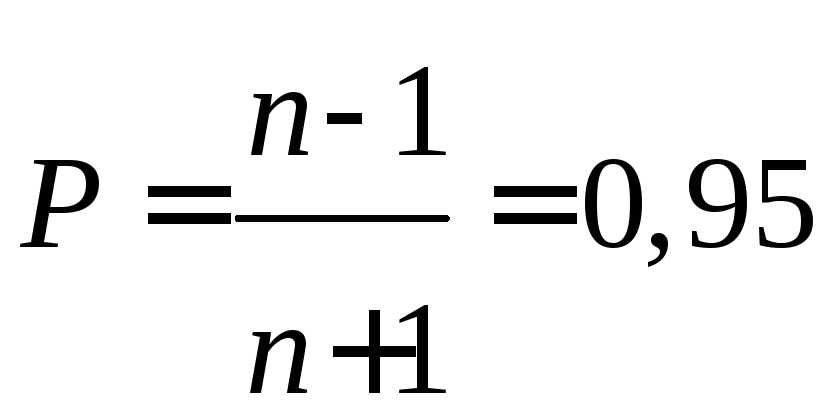при
n=40).
Пример.
Для числа измерений n=10
получена оценка СКО:S=0,2.
Определить границы интервала 
с вероятностью Р =0,9.
Решение.
n-1=
9; α=1- Р= 0,1; Кχ2н=
=
0,73; Кχ2в
=
=
1,65.
Границы СКО:
σн = Кχ2н ·S = 0,73· 0,2 = 0,15;
σв = Кχ2в·S = 1,65· 0,2 = 0,33.
Определение границ доверительного интервала погрешности измерений
ФВ
Метод измерений
Оператор
Составляющие
погрешности: 
;
и
(
О;
ДОП);
суб.
Систематические погрешности суммируют арифметически:
в
абсолютной форме:
в
относительной форме:
Для случайных погрешностей находят суммарное СКО:
в
абсолютной форме: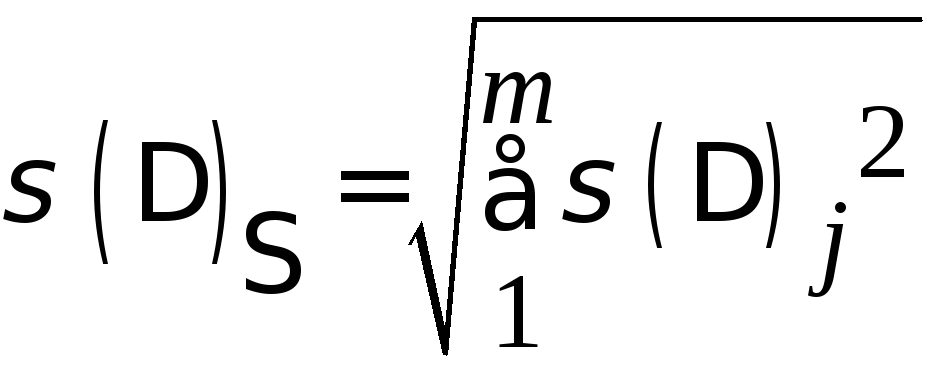 
в
относительной форме: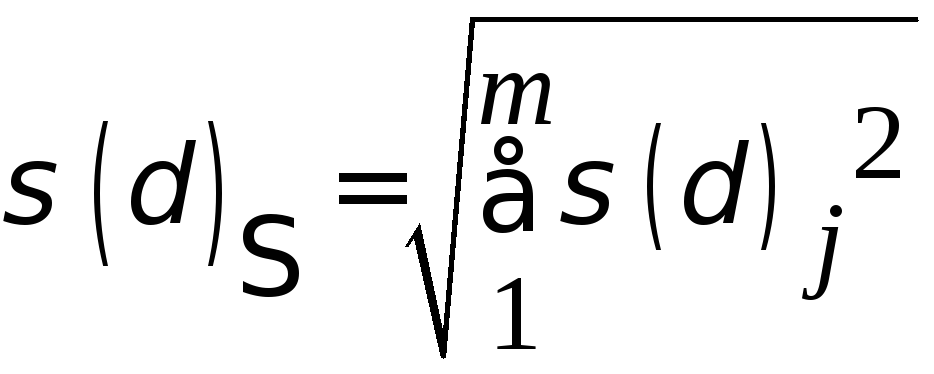 
Границы доверительного интервала:
в абсолютной
форме: 
в
относительной форме: 
При числе составляющих более трех и равномерно распределенных используют формулы:
в
абсолютной форме:
;
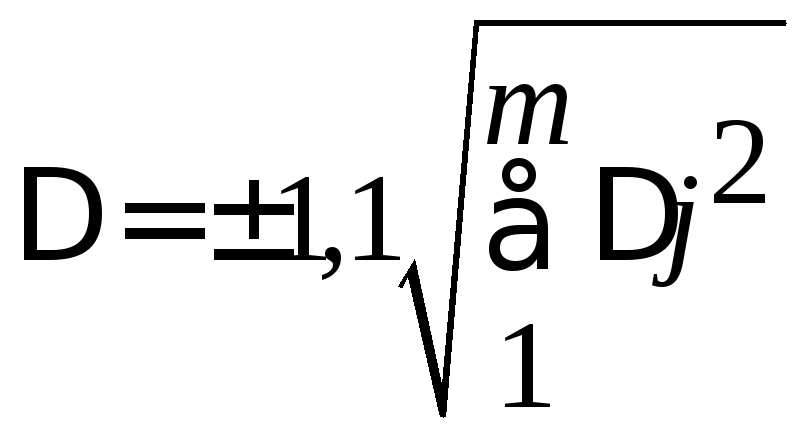Р=0,95,
в
относительной форме:
;
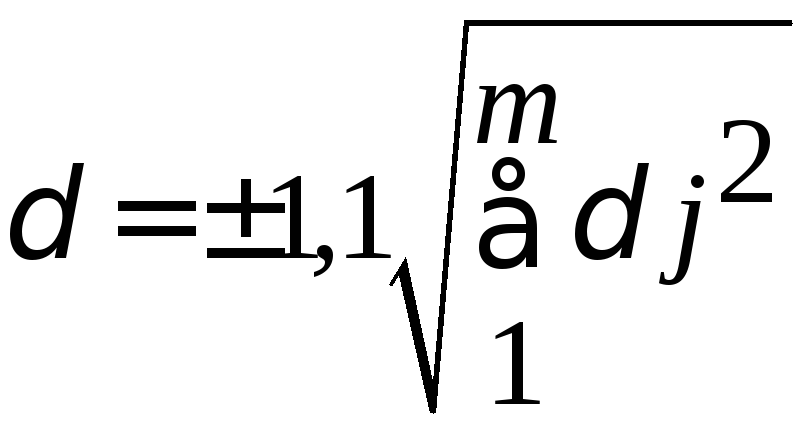Р=0,95.
(Р=0,95)
|
Вероят-ность
|
Значение k для разных законов распределения | ||||||
|
Норм. |
Треуг. |
Трапец. |
Равном. |
А.М. - 1 |
А.М.-2 |
Релея | |
|
2 Р=0,95 |
2 |
1,9 |
1,8 |
1,6 |
1,4 |
1,2 |
2,2 |
|
Р=0,997 |
3 3 |
2,4 |
2,3 |
1,7 |
1,4 |
1,2 |
3,3 |
Пример. СКО основной погрешности СИТ σ[Δ] = 0,15 В; СКО неисключенной систематической погрешности σ[Δ]с=0,09 В. Считая закон распределения нормальным, найти границы погрешности при Р=0,95.
Решение. Вычисляем суммарное СКО:
=
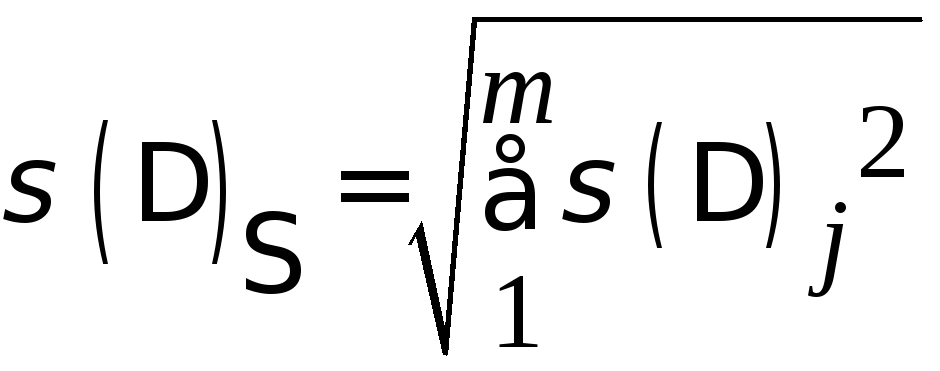В.
Находим границы погрешности, приняв k =2 для Р=0,95:
=
2·
0,18 =
0,36
В; Р=0,95.
Пример. СКО основной погрешности СИТ σ[Δ] = 0,15 В; СКО дополнительной температурной погрешности σ[Δ]t=0,20 В; СКО дополнительной погрешности из-за влияния электромагнитных полей σ[Δ]м = 0,03 В; М[Δ]= 0. Считая закон распределения нормальным, найти границы суммарной погрешности.
Решение. Вычисляем суммарное СКО:
=
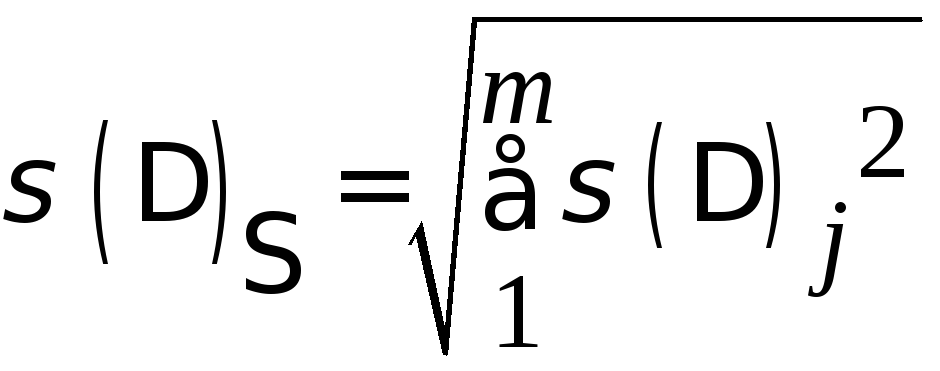=0,25 В;
Находим границы погрешности, приняв k =2 для Р=0,95:
=
2·
0,25 =
0,5
В; Р=0,95.
Пример.
Класс
точности
вольтметра
1,0;
,
верхний предел измерения
Хк=100
В. Температура
воздуха от 15 оС
до 38 оС.
Цена деления 0,5 В. Результат измерения:
Х=84,0
В.
Дополнительная температурная погрешность
не превышает основной на каждые 10 оС
отклонения температуры от нормального
значения. Дополнительная погрешность
из-за
влияния электромагнитных полей
Δм
=
0,4
В. Определить границы погрешности и
представить результат измерения с
вероятностью Р=0,95.
Решение:
Основная
погрешность:
В.
Температурная погрешность:
.
Погрешность считывания показаний:
.
Границы погрешности:
;
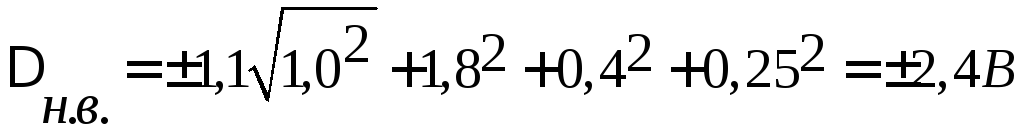Р=0,95
Результат
измерений: (84,0
2,4)
В; Р=0,95.