
- •Погрешности измерений, классификация, характеристики и оценивание
- •5. Границы доверительного интервала:
- •Оценивание характеристик погрешностей
- •Определение границ доверительного интервала погрешности измерений
- •Обработка результатов прямых измерений с многократными наблюдениями
- •Исследование основной погрешности нси в точке диапазона измерений
- •Обработка результатов косвенных измерений
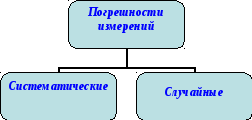
Погрешности измерений, классификация, характеристики и оценивание


Х=Х*+![]()
ФВ
Х* Х= Δ+Х*
![]() ;
; ;
;










 Δ
Δ
Поправка
С= -![]()
Δс Δ0 Хиспр=Х+С
Классификация погрешностей
|
Критерии деления |
Наименование погрешностей |
Примечание
| |
|
измерений |
СИТ | ||
|
По источникам возникновения
|
Методическая Δм Инструмент Δи Субьективная Δс |
Инструмент Δи
|
Δ= Δм*Δи* Δс *-символ объединения |
|
В зависимости от условий измерений |
------------
|
Основная Дополнительные Функции влияния |
См. РД50-453
|
|
По характеру проявления |
Системат.
Δс,
Случайн.
Δ0,
|
Системат
Δс, Случайная
Δ0, |
Грубые промахи исключают |

-точность, 1. Мат. ожидание:
М[Δ]
=
![]()
-достоверность 2. Дисперсия:
D[Δ] = M[(Δ)- M(Δ))2]
-правильность 3.СКО:
σ[Δ]=+![]()
-сходимость 4.Размах:
-воспроизводимость
R
=
![]() ;
;
5. Границы доверительного интервала:
![]() М[Δ]
М[Δ]
![]() -
-![]() 0
+
0
+![]()
Х; Δ от
Δн
до Δв;
Р
Х![]() Δ;
Р
Δ;
Р
Выражение характеристик погрешностей (МИ 1317-86)
|
Классификация |
Наименование |
Обозначен |
Примечание
|
|
Номенклатура характеристик |
СКО |
σ[Δ] |
(см. ссылку) |
|
Нормы погрешностей |
Предел доп. знач. СКО |
σр[Δ]
|
В ТЗ на МВИ |
|
Приписанные характеристики |
Наибольшее возм. значение СКО |
σм [Δ]
|
В МВИ
|
|
Статистические оценки
|
Оценка СКО Границы дов.интерв |
ΔН, ΔВ; Р |
В протоколе измерений
|
Способы представления результатов измерений
|
Вид формы |
Форма представления РИ |
Примечание |
|
Статистическая |
Х;
закон распределения |
При использовании совместно с другими результатами |
|
Интервальная |
Х Х; Δ от Δн до Δв;Р |
Окончательный результат |
Погрешность РИ выражают, как правило, одной значащей цифрой. Две значащие цифры сохраняют: при точных измерениях; если первая цифра не более трех; если предел допускаемой погрешности задан двумя цифрами.
Пример
записи: (15,75![]() 0,34)
В; или 15,75
В
0,34)
В; или 15,75
В![]() 0,34
В; (необходим
пробел); 110;
220 В (для
группы результатов ед. измер. - в конце);
0,34
В; (необходим
пробел); 110;
220 В (для
группы результатов ед. измер. - в конце);
97 мм; Δ от -1 до +2 мм; Р=0,95 ( ед. измер. - в конце).
Пример.
Прибор кл.т.
0,5;
γ=
![]() 0,5%;
ХN
=100
дел.
Насколько
δ
в отметке 30 больше, чем в конце шкалы?
0,5%;
ХN
=100
дел.
Насколько
δ
в отметке 30 больше, чем в конце шкалы?
Решение.
δ30
= γ ХN
/
Х =
![]() 0,5·100
/ 30 =
0,5·100
/ 30 =
![]() 1,6%;
δ100=
1,6%;
δ100=
![]() 0,5%.
0,5%.
Пример.
Погрешности
приборов Δ1
= Δ2
=![]() 0,1
В; ХN1
=100
дел. ХN2
=
50 дел. Показания какого из приборов
более точные?
0,1
В; ХN1
=100
дел. ХN2
=
50 дел. Показания какого из приборов
более точные?
Решение.
γ1=
![]() 0,1·100/100
=
0,1·100/100
=
![]() 0,1%;
γ2=
0,1%;
γ2=![]() 0,1·
100/50 =
0,1·
100/50 =![]() 0,2%.
0,2%.
Пример. Напряжение измерили двумя приборами:
кл.т. 1,0; γ=
 1,0%;
Хк=
300 В; Х=150 В.
1,0%;
Хк=
300 В; Х=150 В.кл.т. 1,5; γ=
 1,5%;
Хк=
200 В; Х=150 В.
1,5%;
Хк=
200 В; Х=150 В.
Относительная погрешность какого из показаний меньше?
Решение.
Δ1=
γ1Хк/100=![]() 1,0
300/100=
1,0
300/100=![]() 3
В;
Δ2=
γ2
Хк/100
=
3
В;
Δ2=
γ2
Хк/100
=
![]() 1,5
200/100=
1,5
200/100=![]() 3
В;
δ1=
δ2=
3
В;
δ1=
δ2=![]() 2%.
2%.
Пример. При поверке прибора кл.т. 2,5 с пределом измерений ХN =100 В в точке шкалы 80 В получены показания РЭ: ХБ=77 В; ХМ = 78 В. Оценить годность прибора.
Решение.
Δ = γ ХN
/100
=![]() 2,5
В.
ΔБ=
80-77=+3
В. Не
годен.
2,5
В.
ΔБ=
80-77=+3
В. Не
годен.
Пример.
Поверяется прибор кл.т. 2,5;( γ=
![]() 2,5%);
Хк
=
30 В. РЭ кл.т. 0,5; ;( γ=
2,5%);
Хк
=
30 В. РЭ кл.т. 0,5; ;( γ=
![]() 0,5%);
Хк
=
30 В. Как учесть погрешность РЭ, чтобы
не забраковать годный прибор?
0,5%);
Хк
=
30 В. Как учесть погрешность РЭ, чтобы
не забраковать годный прибор?
Решение.
Δси
= γ Хк
/100
=![]() 0,75
В; Δо
= γо
Хк
/100=
0,75
В; Δо
= γо
Хк
/100=![]() 0,15
В; Новый допуск: Δси*
=
0,15
В; Новый допуск: Δси*
=
![]() (Δси
-
Δо)
=
(Δси
-
Δо)
=
![]() (0,75-0,15) =
(0,75-0,15) =![]() 0,6
В.
0,6
В.
Виды законов распределения погрешностей
Нормальный закон распределения

Плотность
вероятности: ,
,

Вероятность
попадания погрешности на интервал
![]() :
:
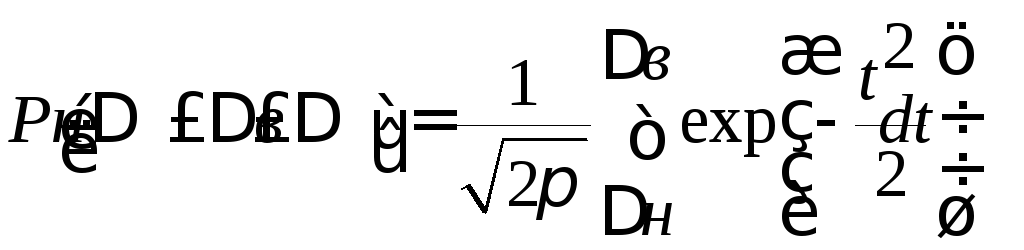 ,
,
Границы интервала абсолютной погрешности измерений:
![]() нв
= М[Δ]
нв
= М[Δ]
![]() σ[Δ]; Р
σ[Δ]; Р
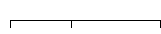

![]() М[Δ]
М[Δ] ![]()
![]() =
= ![]() σ[Δ]; Р
σ[Δ]; Р
-![]() 0
+
0
+![]()
Границы интервала относительной погрешности:
![]() нв
= М[
нв
= М[![]() ]
]
![]() σ[
σ[![]() ]; Р
]; Р
![]() =
= ![]() σ[
σ[![]() ]; Р
]; Р
( t=2 при Р=0,95; t=3 при Р=0,997)
Пример.
1)
![]() =
=![]() 1,2 А; 2)
1,2 А; 2)
![]() =
=![]() 1,4%.
Определить СКО (Р=0,95)
1,4%.
Определить СКО (Р=0,95)
Решение.
σ[Δ]=
![]() =
1,2 / 2
= 0,6 А;
σ[
=
1,2 / 2
= 0,6 А;
σ[![]() ]=
]=![]() =
1,4 / 2
= 0,7 %
=
1,4 / 2
= 0,7 %
Равномерный закон распределения
Этому закону подчиняются: основная погрешность серийно выпускаемых СИТ; погрешности отсчета показаний СИТ; погрешности округления; неисключенный остаток систематической погрешности.
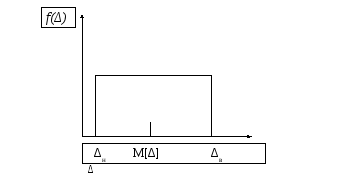
М[Δ]
=
![]() (
(![]() );
σ[Δ]=
);
σ[Δ]=
![]()
Границы интервала абсолютной погрешности:
![]() нв
=
М[Δ]
нв
=
М[Δ]
![]() k·
σ[Δ];
Р
k·
σ[Δ];
Р
![]() =
=
![]() k
·σ[Δ];
Р
k
·σ[Δ];
Р
Границы интервала относительной погрешности:
![]() нв
=
М[
нв
=
М[![]() ]
]
![]() k·
σ[
k·
σ[![]() ];
Р
];
Р
![]() =
=
![]() k·σ[
k·σ[![]() ];
Р
];
Р
( k=![]() при Р
=
1;
k=1,7
при Р
=0,997;
k=1,6
при Р
=0,95)
при Р
=
1;
k=1,7
при Р
=0,997;
k=1,6
при Р
=0,95)
Пример.
Напряжение измеряют вольтметром кл.т.
1,0; γ=![]() 1,0%;
Хк=300
В; L=100
дел; Х=220 В. Определить погрешности:
основную
1,0%;
Хк=300
В; L=100
дел; Х=220 В. Определить погрешности:
основную
![]() о;
относительную
о;
относительную
![]() ;считывания
;считывания
![]() сч;
сч;
СКО: σ[Δо]; σ[Δсч] при Р=0,95.
Решение.
![]() о=
о=
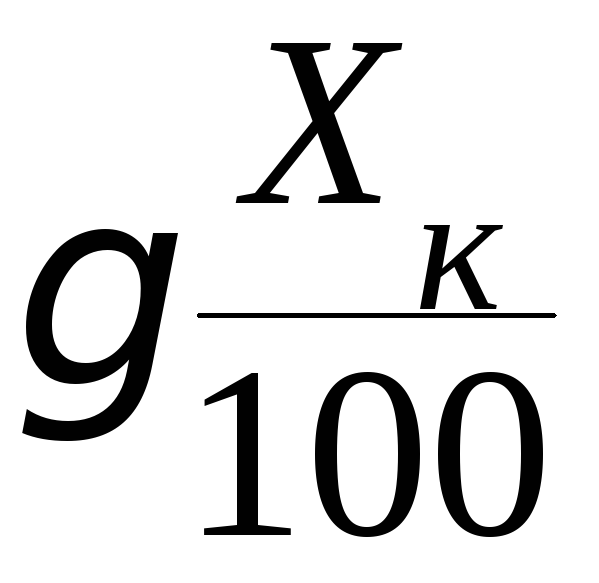 =
=
![]() 1,0
300/100 =
1,0
300/100 =![]() 3
В;
3
В;  =
=
![]() 3 100/220
=
3 100/220
=![]() 1,4%;
е =300/100
= 3
В;
1,4%;
е =300/100
= 3
В;
![]() сч
=
сч
=![]() е/2
=
е/2
=![]() 1,5
В;
1,5
В;
СКО: σ[Δо]=
![]() =3/1,6 = 1,9 В;
σ[Δсч]=
=3/1,6 = 1,9 В;
σ[Δсч]=![]() =
1,5/1,6 =
0,9 В.
=
1,5/1,6 =
0,9 В.
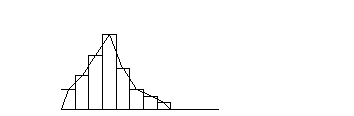
Построение функции распределения по опытным данным
По результатам
Х1;
Х2
··· Хn
определяют
погрешности
![]() 1;
1;![]() 2
···
2
···
![]() n
и
их границы:
n
и
их границы:![]() н
=
н
=
![]() min;
min;
![]() в
=
в
=
![]() max.
max.
Интервал
![]() max
-
max
-
![]() min
делят на k
частей (разрядов) и подсчитывают число
погрешностей в каждом разряде:
min
делят на k
частей (разрядов) и подсчитывают число
погрешностей в каждом разряде:
m1;
m2···
mk;
![]() =n.
=n.
Вычисляют частоту
Рi
=
![]() ;
;
![]() =1 и строят
статистический ряд распределения:
=1 и строят
статистический ряд распределения:
|
Разряд |
|
|
··· |
|
|
Рi |
Рн |
Pi |
··· |
Pв |
 Рi
Рi
Δн Δв
По виду гистограммы подбирают закон распределения.
