2. Связность

Это свойство графов является ключевым при исследовании сетей связи и прежде всего при оценках устойчивости сетей ( систем ) связи и определении качества связи.

Применительно к сетям связи связность характеризуется наличием каналов связи между заданными узлами, их количеством и качественными характеристиками, способностью обеспечивать передачу заданных потоков сообщений с заданными требованиями к качеству связи в условиях различных воздействий противника на узлы и каналы связи.

Для исследования различных характеристик сети на графах вводится неструктурная информация в виде весовых коэффициентов, но и изучение только структурных свойств графов, характеризующих, их связность имеет существенное значение.

Весь предыдущий материал по теории графов является минимальной необходимой базой для исследования сетей связи, анализа заданных сетей и синтеза сетей с заданными свойствами.

Напомним, что граф называется связным, если из любой вершины v_i в любую другую вершину v_j существует путь( маршрут).

При этом некоторые вершины и ребра могут быть особенными.

Так, вершина, удаление которой увеличивает число компонент графа называется точкой сочленения.

Ребро с аналогичным свойством называется мостом.

Неразделимым называется связный, непустой не имеющий точек сочленения граф.

Блок графа- это его максимальный неразделимый подграф.

Полносвязный блок называют кликой.

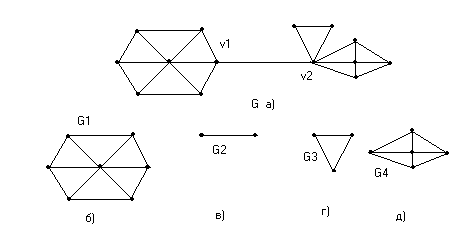
Рис.23. Граф и его блоки. а) граф G, б,в,г,д)- блоки графа G₁ ,G₂ ,G₃ , G₄. v₁ иv₂ – точки сочленения, в) –мост G₂ (ребро <v₁ v₂>). г) и д) – клики G₃ иG₄

Вершинной связностью æ(G) называют наименьшее число вершин, удаление которых приводит к несвязному (пустому) графу.

Реберной связностью λ(G) называют минимальное число ребер, удаление которых приводит к несвязному или тривиальному графу. Другими словами, λ(G)- это число ребер в разрезе с минимальным числом ребер. Для ее определения достаточно рассмотреть базисное множество разрезов.

Смешанная связность σ(G)- минимальное число вершин и ребер, удаление которых приводит к несвязному графу.

Для характеристики смешанной связности σ (G) используют понятие пары связности, под которой понимают упорядоченную пару(a,b) , таких целых неотрицательных чисел, что найдется множество, содержащее а вершин и b ребер, удаление которых делает граф несвязным, и не найдется множества с а-1 вершинами и в ребрами или а вершинами и b-1 ребрами, обладающего этим же свойством. Так, пары (æ,0) и (0, λ)являются парами связностей. Эта функция называется функцией связности графа G.

Вершинная связность важна при оценке живучести в условиях воздействия оружия противника на узлы связи, реберная – при оценке помехозащишености сети, смешанная при воздействии средств РЭБ (помех и оружия) на сети (системы) связи.

Важное значение при изучении связности имеет степень вершин d(v_i) и минимальная степень вершин графа δ(G).

Доказано, что для любого графа выполняются:

æ(G) ≤ λ(G) ≤ δ (G)

кроме того, показано, что ограничения накладываемые на λ, δ и æ нельзя улучшить.

Если же граф G имеет n вершин и δ (G) ≥ [n / 2] ,то λ(G) = δ(G) и наибольшая связность графа равна [2m / n], если m ≥ n-1 .

Рис.24. Граф, для которого æ(G) = 2{v₁ и v₂ или v₇ и v₈},

λ(G) = 3 { <v₁v₇>,<v₂v₇>,<v₂v₈>}, σ (G)= 2 {v₂ и <v₁,v₇>} или {v₇ и <v₂,v₈>}.

С точки зрения воздействия противника это означает, что для нарушения связности сети необходимо:

-уничтожить узлы v₁ и v₃;

-уничтожить узлы v₇ и v₈;

-подавить каналы или уничтожить линии связи, соответствующие на модели ребрам <v₁v₇>, <v₂v₇>, <v₂v₈>;

-уничтожить узел v₂ и подавить <v₁v₇>;

-уничтожить узел v₇ и подавить <v₂v₈>.

Пары связности графа: (0,3); (1,1); (2,0)функция связности показана на рис.25.

σ(æ)
3
2
1
0	1	2		æ

Рис.25. Функция связности F(æ) графа G

Граф называется k- вершинно-связным, если æ(G) ≥ k и k реберно- связным, если λ(G) ≥ k .

Связность графа достаточно жестко коррелируется с числом вершинно и реберно непересекающихся путей, разрезами точками сочления и сечениями по ребрам и вершинам (разделяющими множествами). Рассмотрим эти вопросы более подробно.

Под сечением по вершинам (разделяющим множеством) понимается множество вершин, удаление которых приводит к несвязному графу.

Таким образом, вершинная связность æ(G) является минимальным сечением по вершинам ( разделяющим множеством).

Так на рис.26. сечением по вершинам (разделяющим множеством), может быть множество {v₁, v₂, v₇, v₈}, состоящее из двух минимальных сечений множеств {v₁, v₂} и { v₇, v₈}, определяющих вершинную связность графа.

Пусть u и v- две различные вершины связного графа. u и v, называются вершино- пересекающимися, если у них нет общих вершин, отличных от u и v, и реберно- пересекающимся, если у них нет общих ребер. Множество S вершин, ребер, или ребер и вершин разделяет u и v, если u и v принадлежат различным компонентам графа G-S.

G₁G₂

Рис.26. Граф G(V,E) и разделяющее множество вершин и ребер S.

На рис.1.26. приведен граф G, разделяющее множество S={v₁, v₂, v₇, v₈ и ребра, показанные пунктиром}, и граф G-S содержащий две компоненты G₁ и G₂ с вершинами {v₃, v₄, v₅, v₆} и {v₉, v₁₀, v₁₁, v₁₂} и ребрами, показаными сплошными линиями.

В разделенных компонентах графа G, например G₁ и G₂ рассматривают три пары объектов:

выделенные вершины u и v , например u = v₅; v = v₁₀ ;

произвольные вершины u и v , например, v_i ЄV₁и v_jЄ V₂, где V₁={ v_3, v_4, v_5, v_6,} , V₁={ v_9, v_10, v_11, v_12,}.

два множества вершин V₁ и V₂.

Это разделение можно произвести, удаляя вершины, ребра или вершины и ребра, т.е. тремя способами.

Таким образом, между связностью графа и числом непересекающихся путей в зависимости от способов выделения вершин и разделяющего их множества существуют 9 вариантов взаимозависимостей.

Кроме того, если рассматривать результаты отдельно для ориентированных и неориентированных графов, то их 18.

Все эти варианты Харари выделил в класс теорем Менгера.

Рассмотрим их без доказательства и проиллюстрируем на примерах только основные из них.

Теорема 1. Наименьшее число вершин, разделяющих две несмежные вершины s и t , равно наибольшему числу вершинно- непересекающихся простых (s-t) путей).

Так на рис.38 для вершин s = v₁ , t = v₁₁ наименьшее число вершин, которые их разделяют 3. Это { v_5, v_6, v₇}.

Вершинно – непересекающихся путей также 3. Это один из путей, ведущих из вершины s в t через узлы v₅ , v₆ , v₇;

Рис.27.Граф для иллюстрации класса теорем Менгера.

Пять реберно- непересекающихся путей, приведены ниже:

¹_st= <e₁,e₈,e₁₉> = <v₁,v₂,v₇,v₁₁>

²_st= <e₃,e₁₀,e₂₃> = <v₁,v₆,v₈,v₁₁>вершинно- непересекающиеся пути

³_st= <e₅,e₁₄> = <v₁,v₅,v₁₁>

⁴_st=e₂,e₉,e₁₅,e₁₇,e₂₁>= < v₁,v₃,v₇,v₆,v₉,v₁₁>вершинно- зависимые

⁵_st=<e₄,e₁₁,e₁₈,e₂₂>=<v₁,v₄,v₆,v₁₀,v₁₁>пути

Для реберно- непересекающихся путей ⁴_st , ⁵_st существуют общие с ¹_st, ²_st вершины v₆ и v₇.

Общие для путей вершины обведены пунктиром.

Теорема 2. Граф k- связен тогда и только тогда, когда любая пара вершин соединена по крайней мере kвершинно- непересекающимися путями.

Связь между теоремами 1 и 2 устанавливается, если ввести понятие локальной связности.

Локальной связностью æ(u, v) двух несмежных вершин, u и v графа G называется наименьшее число вершин, удаление которых разделяет u и v .

В этом случае для произвольных вершин u и v справедливо равенство æ(u, v) = ₀(u,v), где ₀(u,v)- наибольшее число вершинно-непересекающихся путей, соединяющих u и v.

Для неполных графов G соотношение, связывающее теоремы 1 и 2 имеет вид: æ(G) = min æ(u, v), где минимум берется по всем парам несмежных вершин u и v.

Для полного графа это равенство справедливо всегда.

Возьмем произвольные несмежные вершины u = v₁ и v = v₇. (рис.27.)

Определим ₀(u,v) :

u = v₁ v₂ v₇= v; u = v₁ v₃ v₇= v; u = v₁ v₆ v₇= v; u = v₁ v₄ v₇= v; u = v₁ v₅ v₁₁ v₇= v ₀(u,v) = 5, это вполне очевидно, поскольку из вершины u, исходит только 5 ребер к независимым вершинам;

F(u) = { v₂, v₃, v₄, v₅,v₆}, степень d(u)=5.

Пусть теперь u = v₃ , v = v₄. Определим ₀(u,v);

u = v₃ v₂ v₄= v; u = v₃ v₁ v₄= v; u = v₃ v₇ v₄= v ₀(u,v)= 3

Это тоже ожидаемый результат, поскольку степень вершины d(v₃) = 3, следовательновершинно-независимых путей, исходящих из нее, не может быть более трех.

Вершина v₄ имеет степень d(v₄) = 5 и поэтому не накладывает ограничений .

Возьмем в качестве несмежных вершины с минимальными степенями.

Это вершины u = v₃ и v = v₈ и определим ₀(u,v);

u = v₃ v₇ v₈= v; u = v₃ v₆ v₈= v; u = v₃ v₁ v₅ v₁₁ v₈ = v

Вершина v₃ имеет степень d(v₃)=3 и связана с вершинами {v₁ v₆ v₇}; v = v₈ также имеет степень d(v₈)=3 и связана с вершинами v₆ , v₇ ,v₁₁.

Вершины v₆ и v₇ являются смежными и для v = v₈ .

Для того, чтобы эти вершины были связаны тремя независимыми путями, необходимо, чтобы вершина v₁, смежная с вершиной v₃ и вершина v₁₁, смежная с v₈ были связаны вершинно-независимыми путям.

Такой путь есть v₁ , v₅ ,v₁₁ , причем вершина v₅ не входит в первые два пути.

Для двух несмежных вершин с минимальными степенями получено ₀(u,v), равное наибольшему числу вершинно- независимых путей 3.

Следуя теореме 2, можно заключить, что граф на рис.27. является 3- связным (вершинно), т.е. æ(G) = min æ(u, v)= 3 ,и кроме того показано, что æ(G) ≤ δ(G) = min d(v_i)=3; в данном случае имеет место равенство.

Таким образом, соотношение æ(G) = min æ(u, v), связывающее теоремы 1 и 2, кроме того устанавливает зависимость между глобальными æ(G) и локальными æ(u, v) характеристиками вершинной связности.

Следует обратить внимание на то, что во-первых необязательно минимальное число независимых путей находится между вершинами с минимальными степенями и во-вторых, задача определения минимального локального показателя связности, а следовательно и связности не является тривиальной.

Рассмотрим пример на рис.28, где показаны два изоморфных графов G₁, G₂

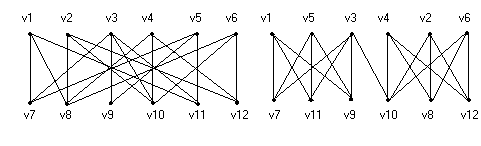
G₁ G₂

Рис.28. Графы G₁ и G₂ для иллюстрации сложного случая определения æ(G) и min æ(u, v).

Изоморфность проверяется подстановкой:

t= 1 2 3 4 5 6 7 8 9 10 11 12

1 5 3 4 2 6 7 11 9 10 8 12

Каждая из вершин, кроме v₃ и v₁₀, имеет степень 3, а вершины v₃ иv₁₀ имеют степень 4.

Вместе с тем , вершины v₃ и v₁₀ являются точками сочленения, а ребро <v₃ и v₁₀> - мостом, так что вершинная и реберная связности равны 1, т.е. æ(G) =λ(G)= 1, кроме того σ(G)= 1. При этом пара связности (а,в) равна(1,0) или (0,1), т.е. необходимо удалить либо одну вершину(v₃ или v₁₀) или одно ребро <v₃v₁₀>.

Теорема 3. Для любых двух вершин графа наибольшее число реберно – непересекающихся путей, соединяющих их, равно наименьшему числу ребер, разделяющих эти вершины.

Из рис.27. видно, что вершины s и t можно разделить , удалив 5 ребер и не меньше, и что наибольшее число непересекающихся по ребрам (s – t) путей равно 5.

Проиллюстрируем это.

Из вершины s = v₁ исходит ровно 5 ребер E₁= { e₁, e₂, e₃, e₄, e₅}. В вершину t = v₁₁ заходят ровно 5 ребер E₂= { e₁₉, e₂₃, e₂₁, e₂₂, е₁₄ }.

Между вершинами s и t существуют следующие реберно- независимые пути, включающие ребра множества Е₁, в качестве начальных и ребра множества Е₂ в качестве конечных.

^1st = e₁ e₈ e₁₉

²_st = e₃ e₁₀ e₂₃

³_st = e₅ e₁₄

⁴_st= e₂e₉e₁₅e₁₇e₂₁

⁵_st = e₄e₁₁ e₁₈ e₂₂

Е₁Е₂

Множества Е₁ и Е₂ обведены пунктирными линиями. Остальные ребра путей ⁱ_st (i =1, 5) также являются различными.

В пути ¹_st ребро е₈ можно заменить ребрами е₇е₁₅, т.е. между множествами Е₁ и Е₂ существует более 5 реберно- независимых путей, поэтому наименьшее число ребер, определяющих число реберно- непересекающихся путей в данном случае определяется минимальной степенью вершин s и t .

В данном случае обе они равны 5, следовательно вершины s и t можно разделить, удалив 5 ребер и наибольшее число непересекающихся по ребрам (s – t ) путей также равно 5, что подтверждает правильность теоремы 3.

Поиск и определение реберно–независимых путей важен прирешения задачи оценки вероятности передачи сообщений, следующих в потоке заданной интенсивности, за время не более требуемого в условиях подавления каналов радиосвязи помехами.

Теорема 4. Для любых двух непересекающихся непустых множеств вершин V₁ и V₂ наибольшее число вершинно- непересекающихся путей, соединяющих V₁ и V₂ равно наименьшему числу вершин, разделяющих V₁ и V₂ , при условии, что ни одна из вершин множества V₁ не должна быть смежной с вершинами множества V₂ .

На рис 38 условиям теоремы 4 соответствуют множества;

V₁= {v₁, v₂, v₃, v₄}

V₂= {v₈, v₉, v₁₀, v₁₁}

Множество V₃= {v₅, v₆, v₇ }, разделяющее множества V₁ и V₂,включает три вершины, через которые проходят три вершинно- независимых пути, соединяющих вершины множеств V₁ и V₂, и других вершинно – независимых путей нет.

Возьмем в качестве другого примера V₁= {v₂, v₃, v₆, v₇}, которому по условиям теоремы 4 может соответствовать только множество V₂= {v₅}.

Множество V₃ , разделяющее множества V₁ и V₂, включает 6 вершин V₃= {v₁, v₄, v₆, v₉, v₁₀,v₁₁}однако, минимальное число вершин, которое разделяет множества V₁ и V₂ –это множество вершин, смежных с v₅ {v₁,v₄,v₁₀,v₁₁}содержит 4 вершины, следовательно и число вершинно-независимых путей из множества V₁ в V₂ равно 4.

Определение числа вершинно-независимых путей важно при моделировании поведения сети в условиях огневого воздействия противника на узлы связи.

С помощью теорем 1- 4 устанавливаются два понятия связности – вершинная æ(G) и реберная λ(G), а также определяются их взаимозависимости, т.е. каждый граф можно характеризовать парой связностей, точно также можно ввести понятие ‘’ пары связностей’’ для двух выделенных вершин u и v .

Следующая теорема устанавливает количественные зависимости между составляющими введенного понятия смешанной связности σ(G).

Теорема 5. Упорядоченная пара (а,в) является парой связности для вершин u и v графа G тогда и только тогда, когда существует а вершинно- непересекающихся (u-v) путей, и в реберно- непересекающихся (u-v) путей не имеющих общих ребер с а предыдущими путями и, кроме того, наибольшие возможные числа таких путей равны именно а и в.

На графе рис.27. между вершинами S и t существуют, как было показано ранее, 5 реберно – независимых путей:

¹_st = < e₁, e₈ ,e₁₉><v₁, v₂, v₇,v₁₁ >

²_st = < e₃, e₁₀ ,e₂₃><v₁, v₆, v₈,v₁₁ >

³_st = < e₅, e₁₄><v₁, v₅, v₁₁>

⁴_st = < e₂, e₉ ,e₁₅, e₁₇ ,e₂₁><v₁, v₃, v₇, v₆, v₉, v₁₁ >

⁵_st = < e₄, e₁₁ ,e₂₂, e1₈ ><v₁, v₄, v₆,v₁₀ , v₁₁ >

При этом, первые три пути являются и вершинно- независимыми, проходящими через вершины {v₅, v₆, v₇ }, которые составляют минимальное сечение по вершинам, т.е. определяют вершинную связность графа æ(G).

Это означает, что в данном случае λ(G)=5, æ(G) =3 и упорядоченные пары (0, λ), (æ, 0) являются парами связностей для вершин S и t (v₁и v₁₁).

Построим функцую связности для вершин s и t :

σ(æ)	λ(s,t)
5	(5, 0)
4	(4, 1)
3		(3, 2)
2
1		(0, 3)	æ(s,t)

0 1 2 3

Рис.29. Функция связности σ (s,t)

Координаты функции связности для вершин (s,t) показывают, сколько вершин и ребер нужно изъять, чтобы нарушить связность между этими вершинами. Всего таких пар æ + 1, в нашем примере их 4.

Так, из рис.1.28. видно, что при сохранившихся вершинах {v₅, v₆, v₇}, необходимо нарушить все ⁱ_st путей (i=1,5).

При удалении одной из трех вершин, необходимо нарушить 4 пути, при удалении 2 вершин –3 пути, а при удалении всех 3^х вершин автоматически нарушается все 5 реберно – независимых путей.

Теорема 6: В каждом графе наибольшее число реберно- непересекающихся реберных разрезов, разделяющих две вершины u и v, равно наименьшему числу ребер простого пути, соединяющего u и v, т.е. равно расстоянию (выраженному через минимальное число ребер) между этими вершинами, т.е. d(u,v).

Например на графе рис.28 наибольшее число реберно- непересекающихся разрезов между вершинами S(v₁ ) и t(v₁₁) равно 2,т.к минимальный путь (цепь), состоит из 2^х ребер е₅ и е₁₄ (³_st = <e₅ , e₁₄> ).

Такими сечениями являются:

S₁= < e₁ ,e₂ ,e₃ ,e₄ ,e₅> и S₂= < e₁₄ ,e₁₉ ,e₂₁ ,e₂₂ ,e₂₃>

Все остальные сечения будут содержать одно из ребер е₅ или е₁₄ .

Способы перечисления путей и сечений изложены ранее. И так имея набор всех путей между произвольными вершинами, не представляет особого труда отобрать из них вершинно- и реберно- пересекающиеся и провести структурный анализ как глобальной, так и локальной связности.

Проще всего анализ начать с выявления мостов и точек сочленения.

Выявление точек сочленения и мостов производится по одному алгоритму:

1.i=1, n (для мостов j=1, m).

2.Удалить вершину v_i (ребро е_j).

3.Проверить связность графа.

4.Если нет, то v_i (е_j) точка сочленения (мост) выполнить 5, иначе выполнить пункт 6.

5.Подсчитать точки сочленения (мосты).

6.Восстановить вершину v_i (ребро е_j).

7.Вывод результатов.

Простейший способ устранения точек сочленения и мостов заключает в том, что в компонентах связности G₁ и G₂ графа G, полученных после удаления точки сочленения (моста), определяют вершины d_imin(G₁) и d_imin(G₂) и соединяют их ребром.

Поскольку в алгоритме поиска точек сочленения (мостов) встречается процедура проверки связности, то необходимо выбрать алгоритм проверки связности, работающий наиболее эффективно.

Кроме того этот алгоритм будет встречаться и при изучении других вопросов, поэтому остановимся на нем несколько подробнее.

Одним из наиболее экономичных (быстрых) алгоритмов определения связности является алгоритм Уоршелла. Алгоритм Уоршелла (Warshall) предназначен для определения связности графов. Он преобразует матрицу смежности А(ij) в матрицу наличия прямых или транзитных путей соответствующим переписыванием матрицы А(ij), поэтому говорят, что алгоритм работает “на месте”. Каждая вершина обрабатывается один раз, поэтому задача решается за один проход. Достоинством алгоритма является достаточно высокая скорость работы, недостатком - отсутствие контроля числа транзитов в пути, если для этого не принять специальных мер. Число транзитов может измениться от 0 до n-1. Результирующая матрица показывает, есть ли путь между произвольными вершинами исходного графа.

Суть алгоритма Уоршелла заключается в следующем. Задается исходный граф G, размерностью nxn. Алгоритм строит последовательность таких графов, что Gⁱ≤ Gⁱ⁺¹ , т.е. граф Gⁱ является подграфом Gⁱ⁺¹ , а исходный граф G = G⁰ , 0≤ i ≤ n-1. Граф Gⁱ (i ≥ 1) получается из графа G^i-1 после обработки вершины i в графе G^i-1. Обработка вершины i в графе G^i-1 включает добавление новых ребер в G^i-1 следующим образом. Пусть в графе G^i-1 присутствуют ребра <i, k>, <i, ℓ >, <i, m>, исходящие из вершины i ,тогда для каждого ребра <j, i>, заходящего в вершину i добавляют в графе G^i-1 ребра <j, k>, <j, ℓ >, <j, m>, если они еще не присутствовали в графе G^i-1 .

Таким образом, описание алгоритма можно представлять следующим образом.

1.Ввести матрицу смежности графа A(i, j)

2.Положить i =1 до n

3.Положить j =1 до n

4.Если элемент матрицы смежности a( i, j ) равен нулю то перейти к 8

5.Положить k =1 до n

6.a( j, k ) = a( j, k ) or a( i, k )

7.Положить k = k+1, если k <= n, то перейти к 5

8.Положить j = j+1, если j<= n, то прейти к 3

9.Положить i = i+1, если i<= n то перейти к 2

10.Результирующую матрицу проверить на полную связность.

Работу алгоритма Уоршелла рассмотрим на примере:

G⁰ G¹

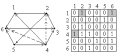
i=1 <i, k >:< 1, 2 >;< 1, 6 >

<j, i>:< 4, 1 >

<j, k >: < 4, 2 >;< 4, 6 >

G¹ G²

i=2 <i, k >:< 2, 5 >

<j, i>:< 1, 2 >;<3,2>;<4,2>

<j, k >:< 1, 5 >;< 3, 5 >;<4,5>

G² G³

i=3 <i, k >:< 3, 2 >;< 3, 5 >

<j, i>:< 4, 3 >;< 6, 3 >

<j, k >: < 4, 2 > ;< 4, 5 >

<6, 2><6,5>

G³ G⁴

i=4 <i, k>:< 4, 1 >;< 4, 2 >;<4,3>

< 4, 5 >;< 4, 6 >

<j, i>:< 5, 4 >

<j, k>:< 5, 1 >;< 5, 2 ><5,3>

< 5, 4 >; < 5, 6 >

G⁴G⁵

i=5 <i, k>:< 5, 1 >;< 5, 2 >;<5,3>

< 5, 4 >;< 5, 6 >

<j, i>:< 1, 5 >;< 2, 5 >;<3,5>

< 4, 5 >;< 6, 5 >

<j, k>:< 1, 2 >;< 1, 3 >;<1,4>

< 1, 6 >;< 2, 1> ;<2,3>;

<2,4>;<2,5>;< 2, 6>;<3,1>;<3,2>;<3,4>;<3,5>;<3,6>; <6,1>;<6,2>;<6,3>; <6,4>;<6,5>

G⁵G⁶

При i = 5 получен полносвязный ориентированный граф, эквивалентныйнеориентированному.

Ребра <i, k>-исходят из i-й вершины

Ребра <j, i>-заходят в i-ю вершину

Ребра <j, k>-добавляют к ребрам графа G^i-1, если их не было ранее

Добавляемые ребра <j, k> на каждом этапе показаны пунктиром.

На этом работа алгоритма заканчивается.

Лекция 11

СИНТЕЗ СЕТЕЙ С МАКСИМАЛЬНОЙ СВЯЗНОСТЬЮ