1. Матрица циклов и ее связь с матрицей инцидентности.
Циклы графов, пронумерованные определенным порядком, можно представить матрицей циклов С.
|
|
|
е1 |
е2 |
е3 |
е4 |
е5 |
|
|
С1 |
1 |
1 |
0 |
1 |
0 |
|
С= |
С2 |
0 |
1 |
1 |
0 |
1 |
|
|
С3 |
1 |
0 |
1 |
1 |
1 |
Матрица циклов имеет m столбцов(по числу ребер ) и количество строк, равное числу циклов (m-n+1).
Матрицу циклов называют еще цикломатической матрицей.
Строку матрицы С: называют также циклическим вектором графа G. Как видно из матрицы циклов, вектор С3 = С1 С2 =11010 01101 = 10111, является линейной комбинацией векторов С1 и С2.
Это означает . что из множества всех циклических векторов можно выделить базисные, по отношению к определенному остовному дереву.
Пусть это дерево состоит из ребер {e1, e2 ,e3 }, тогда хордами будут ребра е4 и е5 . Вспомним , что базисный цикл состоит из одной хорды и ветвей остовного дерева. Переставим столбцы матрицы циклов так, чтобы первым строкам и столбцам соответствовали хорды остовного дерева:
|
|
|
е4 |
е5 |
е1 |
е2 |
е3 |
|
Сf= |
е4 |
1 |
0 |
1 |
1 |
0 |
|
|
е5 |
0 |
1 |
0 |
1 |
1 |
I Сft
Таким образом, базисная матрица циклов Сf является подматрицей матрицы циклов C и включает только циклы, определяемые хордами выбранного остовного дерева.
Эту матрицу можно записать в виде :Сf= [ I | Cft ], где I – единичная матрица хорд, а элементами матрицы Cft являются ветви выбранного остовного дерева, по отношению к которому определены базисные циклы.
Кроме того, матрицу Сf можно представить состоящей из двух блоков Cf = (С11 С12) , где С11= I , С12= Cft.
Запишем матрицу инцидентности графа G, переставив столбцы, как и у базисной матрицы циклов:
|
|
|
е4 |
е5 |
е1 |
е2 |
е3 |
|
|
V1 |
0 |
0 |
1 |
1 |
1 |
|
A= |
V2 |
1 |
0 |
1 |
0 |
0 |
|
|
V3 |
1 |
1 |
0 |
1 |
0 |
|
|
V4 |
0 |
1 |
0 |
0 |
1 |
Так как ранг матрицы инцидентности равен n-1 , где n- число вершин, то можно выделить неособенную матрицу в правом верхнем углу А12 размерностью (n-1)х(n-1), состоящую из ветвей остовного дерева( так же ранга n-1) и представить матрицу инцидентности А в виде блочной матрицы:
|
А= |
А11 |
А12 |
, где |
А11= |
0 |
0 |
|
1 |
1 |
1 |
|
|
|
1 |
0 |
; А12= |
1 |
0 |
0 | |||
|
А21 |
А22 |
1 |
1 |
|
0 |
1 |
0 |
А21=| 0 1 | A22= | 0 0 1 |
Матрица А11 представляет кодерево, состоящее из хорд е4 и е5 , матрица А12 представляет дерево по отношению к которому определяются базисные циклы.
Матрицы А21 и А22 линейно зависят от А11 и А12 , выражаются через них в виде суммы элементов строк по модулю 2, что легко проверяется непосредственным сложением. Доказано , что А . С' = 0.
В наших новых обозначениях это выражение можно переписать следующим образом :
А11А12I
А21А22 C12=0
Проверим его непосредственно для графа G:
0 0 1 1 1 1 0 00
А11А12 I 1 0
1 0 1 0 1 00
А∙С
= А21А22 C12= 1
1 0 1 0 х 1 0 = 00 =0.
0 1 0 0 1 1 1 00
0 1 00
Из этого же выражения следует , что :
А11 .I + A12 . C′12 = 0
Поскольку матрица А12 неособенная то :
С12= А12-1 . А11 , т.ематрицу циклов ( транспонированную) можно получить из матрицы инцидентности представив ее в виде блоков, состоящих из подматрицы дерева и подматрицы кодерева, т.е. из ветвей остовного дерева и хорд кодерева.
Рассмотрим пример для нашего графа :
1 1 1 1 0 
А12= 1 0 0 |A12| =-1 х = -1 =1
0 1 0 0 1
Определитель А12 вычислен путем разложения его по элементам третьего столбца, с учетом применения алгебры по модулю 2.
Для обращения матрицы существуют стандартные процедуры (напримерmathcad), но мы воспользуемся классическим методом.
а1а2 а3
в2с3-в3с2
а3с2-а2с3 а1в3-а3в2
А= в1 в2в3; А-1= 1/ |A|в3с1-в1с3а1с3-а3с1 а3в1-а1в3
с1с2 с3 в1с2-в2с1а2с1-а1с2 а1в2-а2в1
подставив в выражение элементы матрицы А12, получим,
0 1 0 1 1
1 
А12-1= 0 0 1 ; проверим А12. А12-1= 1 0 0 х
1 1 1 0 1
0 
0 1 0 1 0 0
х 0 0 1 = 0 1 0
1 1 1 0 0 1
найдем траспонированную матрицу С′12
0 1 0 0 0 1 0 
С′12= А12-1. А11= 0 0 1 . 1 0 = 1 1
1 1 1 1 1 0 1
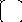
1 1 0
откудаС12= 0 1 1 .
Присоединив слева единичную матрицу, получим матрицу базисных циклов:
1 0 1 1 0
Сf= ( I / C12)=
0 1 0 1 1
Таким образом, задавшись остовным деревом, из матрицы инциденций можно получить матрицу базисных циклов.
Однако, проще это делать “ вручную”:
Пусть остовное дерево включает ветви е1, е2, е3, а хорды кодеревы е4 и е5. Добавляя к дереву хорду е4получаем цикл е2е3е4, добавляя хорду е5, получаем цикл е1е2е5. Получив циклы, записываем их в матрицу циклов.
|
|
e1 |
e2 |
e3 |
e4 |
e5 |
|
Сf= |
1 |
1 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
0 |
1 |
Поскольку остовное дерево все равно необходимо набирать вручную при вводе в ЭВМ, то и матрицу циклов можно сразу набрать вручную, так как при добавлении одной (очередной) хорды получается ровно один (очередной) базовой цикл.