2. Изоморфность графов
Для графов, как и для других геометрических фигур, существует отношение эквивалентности. Если для геометрических фигур устанавливаются отношение равенства, подобия, конгруэнтности, то для графов аналогом таких отношений является понятие изоморфности (изоморфного вложения, наличие изоморфной части двух графов), отражающее степень совпадения структурных свойств двух графов. При этом геометрические размеры, формы представления не играют роли.
Два графа G(X ,F) и H(Y, P) называются изоморфными, если существует взаимно однозначное соответствие между множествами вершин X , Y и множествами ребер F, P , сохраняющее отношение смежности (инцидентности).
Другими словами , если вершинам xi , xj в графе G соответствуют вершины yk , ye в графе H, то ребро (дуга) в G(X , F), имеющие концевые вершины xiи xj , должно соответствовать ребру в H(Y , P) , имеющему концевые вершины yk, ye и наоборот .
На рис.1.9. приведены два изоморфных графа G(X ,F) и H(Y , P)
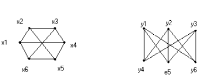
а)G (X , F ) б) H ( Y , P )
Рис.1.9.(а,б). Графы G , H – изоморфны.
Оба графа имеют по 6 вершин , 9 ребер .Степени вершин у всех ребер одинаковы k = 3.
Изоморфизм графов устанавливается подстановкой:
x1 x2 x3 x4 x5 x6
y1 y4 y2 y5 y3 y6
Запишем оба графа в виде списков смежности:
|
X1 |
X2, |
X4, |
X6 |
|
Y1 |
Y4, |
Y5, |
Y6 |
|
X2 |
X1, |
X3, |
X5 |
|
Y2 |
Y4, |
Y5, |
Y6 |
|
X3 |
X2, |
X4, |
X6 |
|
Y3 |
Y4, |
Y5, |
Y6 |
|
X4 |
X1, |
X3, |
X5 |
|
Y4 |
Y1, |
Y2, |
Y3 |
|
X5 |
X2, |
X4, |
X6 |
|
Y5 |
Y1, |
Y2, |
Y3 |
|
X6 |
X1, |
X3, |
X5 |
|
Y6 |
Y1, |
Y2, |
Y3 |
и проверим справедливость подстановки для ребер.
F(x1)<x1,x2><y1,y4>; <x1,x4><y1,y5>; <x1,x6><y1,y6>;
это следует из подстановки:
x1
, x2
, x6
y1 , y4,y6 ;
F(x2)<x2,x1><y4,y1>; <x2,x3><y4,y2>; <x2,x5><y4,y3>,
что следует из подстановки:
x2
, x1,
x3 ,
x5
y4 , y1,y2 , y3
Этих проверок достаточно, поскольку остальные строки в списке смежности идентичны, т.е. индексам 2,4,6 у вершин графа G(X, F) , соответствуют 4,5,6 у вершин графа H(V, P), а индексам 1,3,5 у вершин графа G , соответствуют индексы 1,2,3.
Таким образом, графы G(X, F) и H(Y, P) изоморфны. Как видно из примера, необходимым условиям изоморфности является равенство числа вершин (n), ребер (m), степеней (полустепеней исхода и захода) вершин, которые ставятся в соответствие друг другу.
Понятие изоморфности позволяет распространять некоторые очевидные свойства одного графа на другой.
Так
граф H(Y ,P) на рис.1.9 является двудольным
, т.е. таким графом, множество вершин
которого Y можно разбить на два
непересекающихся подмножества Y' и Y''
(т.е. Y=Y'U Y'',Y'
Y''=
) так , что каждое ребро соединяет
некоторую вершину из Y' с некоторой
вершиной Y''.
В рассматриваемом примере для графа H(Y, P) такими подмножествами являются Y'={y1,y2,y3}, Y''={y3,y4,y5}
В графе G(X , F) им соответствуют подмножества:
X'= { x1 ,x3, x5 }, и X'' ={ x2 ,x4, x6 } поэтому граф G(X, F) также является двудольным. Кроме того , графы G(X , F) и H(Y , P) являются полными двудольными поскольку каждая из вершин одного подмножества соединяется с каждой вершиной другого подмножества, что хорошо видно как из графического представления, так и из представления графов списками смежности.
Под двудольным графом часто понимают граф, в котором заранее заданна определенное количество вершин V' и V'' (доли).
Распространим теперь некоторые вполне очевидные свойства графа G(X,F) на граф H(Y,P). Автоморфизмом графа называют изоморфное отображение графа на себя.
Граф G(X,F) на рис.9а обладает несколькими автоморфизмами . Например , если вращать граф по часовой стрелке , то циклические подстановки дают 6 изоморфных графов
1 2 3 4 5 6
2 3 4 5 6 1
3 4 5 6 1 2
4 5 6 1 2 3
5 6 1 2 3 4
6 1 2 3 4 5
1 2 3 4 5 6
Кроме этих преобразований циклического характера можно произвести вращение графа G(X,F) вокруг ребер <x1,x4>,<x2,x5>,<x3,x6> на 180 с помощью подстановок:
1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 
1 6 5 4 3 2 3 2 1 6 5 3 5 4 3 2 1 6
Как видно из подстановок для ребер, вокруг которых осуществляется поворот на 180 подстановки вершин являются тождественными т.е. у ребра <1,4> вершина 1 отображается в 1 , вершина 4 – в 4 и.т.д.
Прежде чем рассмотреть автоморфизмы графа H(Y,P) введем понятия маршрута, цепи, цикла. Последовательность ребер <v1,v2>, <v2,v3>,….<vs-1,vs> называется маршрутом, соединяющим вершины v1 и vs. Маршрут называется цепью, если все его ребра различны и путем, если все его вершины различны.
Замкнутая (простая) цепь называется (простым) циклом. Число ребер пути называется длиной пути. Число ребер цикла – длиной цикла. Ребро графа G называется циклическим, если в графе существуют цикл, содержащий это ребро. В противном случае ребро называется нециклическим.
Граф называется связным, если любая пара его вершин соединена маршрутом. Простой цикл, содержащий все вершины графа, называется гамильтоновым. Например, цикл <x1, x2>, <x2, x3>, <x3, x4>, <x4, x5>, <x5, x6>, <x6, x7>,<x7, x1> включает все вершины графа G(X , F), поэтому является гамильтоновым.
В графе H(Y ,P) ему соответствует цикл:<y1,y4,y2,y5,y3,y6,y1>
Перерисовав граф H(Y ,P) , так, чтобы гамильтонов цикл был в явном виде, получим изображение как показано на рис.10.
Рис.10. Преобразованный граф H(Y,P)
Циклическую подстановку можно записать в виде:
y1 y4y2y5y3y6
4 2 5 3 6 1
2 5 3 6 1 4
5 3 6 1 4 2
3 6 1 4 2 5
6 1 4 2 5 3
1 4 2 5 3 6
Вращение преобразованного графа H(Y,P) вокруг ребер <y1,y5>, <y2,y6> и <y3,y4> на 180 производится с помощью подстановок:
1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 
1 3 2 6 5 4 3 2 1 5 4 6 2 1 3 3 4 5
Очевидно, кроме этих автоморфизмов существуют еще как минимум два очевидных для исходного графа H(Y,P)(рис 9б)
Это вращение (поворот на 180)вокруг ребра <y2 , y5> и вокруг горизонтальной прямой , рассекающей пополам все ребра .
Это подстановки:
1 2 3 4 5 6 1 2 3 4 5 6 
4 5 6 1 2 3 3 2 1 6 5 4
Этим преобразованиям графа H(Y,P) соответствуют графические изображения на рис.11.
y1
y2
Рис.11. Автоморфизмы вращение графа H(Y,P)
Все варианты графов, получаемые с помощью описанных подстановок, являются изоморфными и получаются соответствующей перенумерацией вершин, а в матрице смежности соответствующей перестановкой строк и столбцов.
Лекция 7
ОРИЕНТИРОВАННЫЕ И НЕОРИЕНТИРОВАННЫЕ ВЗВЕШЕННЫЕ ГРАФЫ, ИХ ВИДЫ, СВОЙСТВА И МЕТОДЫ ФОРМАЛЬНОГО ОПИСАНИЯ.