Раздел 2. Модели и методы исследования структурных свойств сетей связи

ОРИЕНТИРОВАННЫЕ И НЕОРИЕНТИРОВАННЫЕ ВЗВЕШЕННЫЕ ГРАФЫ, ИХ ВИДЫ, СВОЙСТВА И МЕТОДЫ ФОРМАЛЬНОГО ОПИСАНИЯ.

1. Виды и свойства графов.

Граф – множество V (vertex) вершин и набор E (edge) пар вершин-множество ребер.

Пары могут быть упорядоченными и неупорядоченными.

Граф обозначается через G(V , E).

Неупорядоченная пара вершин называется ребром, упорядоченная – дугой. Граф, содержащий только ребра называется неориентированным, содержащий только дуги – ориентированным, содержащий и ребра и дуги – смешанным. Дуга или ребро могут начинаться и заканчиваться в одной вершине. Такая дуга (ребро) называется петлей.

Некоторые вершины могут соединяться более чем одним ребром, или дугой одного направления. В этом случае они называются кратными. Иногда рассматривают только графы, не содержащие петель и кратных ребер.

Граф, не содержащий петель, но допускающий кратные ребра, называют мультиграфом, а граф содержащий петли и кратные ребра, называют псевдографом графом. Графы без петель и кратных ребер называют обыкновенными. В дальнейшем мы эти понятия различать не будем, если это не вызывает недоразумений.

Обычно граф представляется диаграммой, которую и называют графом, т.е. графическим изображением введенного понятия G (V, E) , где:

V- множество вершин;

E – множество ребер.

G₁( V , E ) G₂ ( V , E )

Рис.1. Помеченный G₁ и непомеченный G₂ смешанные графы.

Вершины, соединенные ребром или дугой называют смежными. Ребро (дуга) и любая из его вершин называются инцидентными.

Если два различных ребра инцидентны одной и той же вершине, то они называются смежными. Например, вершины v₁v₂ , v₂v₃ ,v₁v₄смежны, вершина v₃ инцидентна ребру e₄ и дуге е₅ , а ребра е₁ и е₂, инцидентные вершине v₂ – смежны.

Граф называется помеченным (или перенумерованным), если его вершины отличаются одна от другой какими либо пометками, например v₁,v₂,…,v₆.

Так, на рис.1. граф G₁ (V , E) – помеченный граф, а граф G₂(V , E) - нет.

В теории графов граф рассматривается как некоторый комбинаторный объект, в котором не учитываются такие свойства конкретных графов, как природа вершин и ребер, их относительное расположение, кривизна линий, размеры графа ит.д.

Метки вводятся лишь для того, чтобы можно было математически представить различные графы теми или иными способами.

Один из способов представления, а именно графический, был рассмотрен ранее, рассмотрим другие способы.

Матрицей смежности A=|| a_ij|| , соответствующей графу G (V, E) , называют матрицу, у которой элемент a_ij равен 1 (или числу ребер), если между вершиной v_iи v_jсуществует ребро (или несколько) и a_ij =0 , если между вершинами v_i и v_j нет ребер. Пример графа G(V, E) и его матрицы смежности приведен на рис.2.

А=

Рис.2. Граф G(V, E) и соответствующая ему матрица смежности A=||a_ij||

Размерность матрицы смежности равна nn , где n=|V|, т.е. n равно числу элементов во множестве вершин V={v_i}.

В матрице инцидентности B=||b_ij|| граф G(V,E) ,b_ij=1,если вершина v_iявляется начальной для ребра e_j, b_ij= -1 ,если вершина v_i является конечной для ребра e_j и b_ij=0 в противном случае, т.е.

1, если v_i V – начальная вершина для е_i;

B_ij= -1, если v_i V – конечная вершина для е_j;

0 - в противном случае.

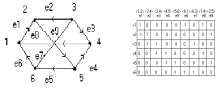
В =

Рис.1.3. Граф G(V, E) и его матрица инцидентности.

Иногда встречаются термины: “матрица смежностей”, “инцидентностей”, “инциденций”, которые употребляются несколько реже.

Если граф неориентированный, то в матрице инцидентности элементы b_ij принимает значение '' 1 '' , если вершина v_i и ребро e_j инцидентны и '' 0 '' в противном случае. Пример:

В =

Рис.1.4.Неориентированный граф и его матрица инцидентности.

Размерность матрицы инцидентности B[n х m] , где n=|V| - число элементов множества V={v_i}, т.е. число вершин, m-число ребер.

Здесь для ребер введены обозначения: e _k=<i,j>.

Для ориентированного ребра (дуги )e_k это означает, что оно начинается в вершине i и заканчивается в вершине j .

Для неориентированного ребра e_k=<i,j>=<j,i> , т.е. порядок следования вершин безразличен.

В верхних частях таблиц инцидентности графов на рис 1.3 и 1.4 дуги и ребра графов e_k заданы списками. Такие списки однозначно определяют граф.

Форма представления графов списками ребер (дуг ) особенно удобна, когда размерность матрицы B[n x m ] велика, а число ребер e_k мало.

Граф на рис.1.3 задается списком ребер G(V,E):<1,2>;<2,1>;<3,4>;<4,5>;<5,6>;<6,1>;<6,3>;<1,4>;<2,5> граф на рис.1.4. задается также <1,2>;<2,6>; <2,5>; <2,4>; <2,3>; <4,5>; <6,5>; <1,6>.

Матрица смежности A представляет из себя множество размерностью VV, каждый элемент которого a_ij может принимать значение 0 или 1 .

Этим самым между элементом a_i (из i-ой строки) и элементом a_j (из j-го столбца) устанавливается бинарное отношение R (relation).

Применительно к теории графов отношение a_i R a_jозначает, что вершина a_i соединяется ребром с вершиной a_j .

Для неориентированных ребер отношение взаимно однозначно, для ориентированных только в том случае , если между вершинами есть дуги противоположной направленности .

В связи с этим различают прямое и обратное отображение для каждой вершины. Это позволяет задать граф с помощью отображения R и R^-1 где R- список вершин в которые отображается данная вершина , а R^-1 список вершин, которые отображаются в данную вершину.

Пусть задан граф G(X ,F) на рис.5 тогда:

F(x₁)={x₂}:F^-1(x₁)={x₅} F(x₂)={x₅}:F^-1(x₂)={x₁,x₃}

F(x₃)={x₂}:F^-1(x₃)={x₄,x₅}

F(x₄)={x₃}:F^-1(x₄)={x₅}

F(x₅)={x₁,x₃,x₄}:F^-1(x₅)={x₂}

Рис.5. Способ задания обыкновенного ориентированного графа G(X, F) с помощью прямого и обратного отображения.

Для неориентированных графов пользуются списком смежности.

Рис.6. Способ задания неориентированного графа списком смежности.

В списке смежности определяется сколько и какие вершины смежны данной вершине.

Для неориентированного графа число ребер, инцидентных данной вершине называют степенью вершины V_i графа G и обозначают d_i, или d(v_i).

Если граф G (без петель ) имеет n вершин и m ребер, то вершина V_i называется изолированной, если d_i =0 и концевой или висячей, если d_i =1.

Граф, у которого все вершины имеют одинаковые степени (равные k) называется регулярным степени k, или гомогенным.

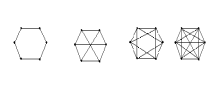
А б в г

Рис.7. Регулярные графы степени k=2,3,4,5

При k = n-1 регулярный граф становится полным, т.е. таким, у которого каждая вершина соединена со всеми другими равно одним ребром.

Графы на рис. 7.а, б, в и г регулярные, со степени k=2,3,4 и 5.

В ориентированном графе G для каждой вершины V_i определяется полу степень исхода и захода как количество дуг, исходящих из вершины V_i и заходящих в нее. Полустепени исхода и захода численно равны мощности множеств прямого и обратного отображений V_iвершин.

Так для графа на рис 5 |F(x₁)|=1 ; |F^-1(x₁)|=1 ; |F(x₂)|=1;

|F^-1(x₂)|=2 ….,|F(x₅)|=3 ; |F^-1(x₅)|=1.

Часто для характеристики вершин ориентированных графов по аналогии с комплексными числами используют составную степень d_i , записываемую одним числом.

Число разбивается на две половины, каждая из которых состоит из одной (для n9), двух (n99), трех(n999) и.т.д позиций, где количество позиций определяется ближайшим большим целым числом к десятичному логарифму количества вершин (n) в графе. Например:

d₁=21

d₂=04

d₃=21

d₄=11

d₅=32

d₆=21

Рис.1.8. Ориентированный граф и составные степени его вершин.

Для графа с числом вершин 99  n  10 составная степень имеет вид a_ia_kb_jb_e; где: a_i, a_k-десятки и единицы числа полустепени исхода,b_j, b_e – десятки и единицы числа полустепени захода.Пусть d₅ = 2236 . Это означает, что из 5-ой вершины исходит 22 дуги и заходит 36.d₁₆₃ = 217613 означает , что из 163-й вершины исходит 217 дуг и заходит 613 ит.д.