Компьютерная графика.

Любая система отображения должна обладать средствами формирования изображений наблюдаемых объектов. Для этого нам понадобится некто (или нечто), «рассматривающий» эти объекты. Этим некто или нечто может быть человек или фотокамера. Именно наблюдатель формирует изображение объектов. Если наблюдателем является человек, то изображение формируется на сетчатке глаза, а в фотокамере — на поверхности фотопленки. Часто понятие объекта и его изображения смешиваются. Мы обычно смотрим на объект с определенной точки и забываем, что другие наблюдатели, рассматривая его из другой точки, могут получить совершенно другое изображение того же самого объекта.

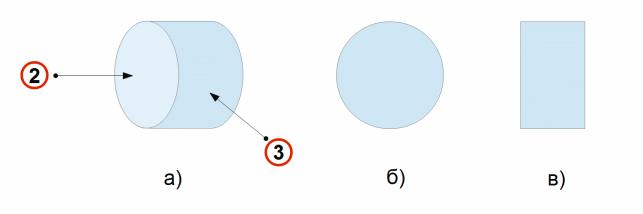
Рисунок 2: Как видят изображения три разных наблюдателя: а — наблюдатель 1, б — наблюдатель 2, в — наблюдатель 3

На рис. 2 а) показано изображение сцены, как ее видит первый наблюдатель. В этой сцене присутствуют два других наблюдателя — второй и третий. Для первого наблюдателя они являются объектами сцены. На рис. 2 б), в) показано, как увидят эту же сцену второй и третий наблюдатели.

Суть процесса формирования изображения и состоит в том, чтобы, зная положение (и характеристики) наблюдателя и положение объекта, описать получаемое при этом двухмерное изображение.

Визуализация изображений.

Наиболее известны два способа визуализации:

•растровый;

•векторный.

Растровый способ визуализации ассоциируется с такими устройствами, как дисплей, телевизор, принтер. Векторный способ используется в векторных дисплеях и плоттерах.

Существуют такие ситуации когда способ описания изображения отличается от способа визуализации. В таких случаях необходимо применять конвертацию. Например, изображение может хранится в растровом виде, а его необходимо вывести на векторный дисплей. Тогда применяется векторизация — преобразование из растрового в векторное описание. Если ситуация обратная, изображение хранится в векторном виде, а необходимо вывести на растровый дисплей, применяется растеризация.

-8-

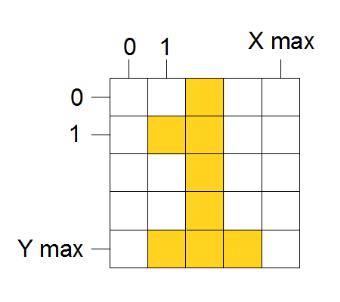
Компьютерная графика.

Растровая визуализация.

Растровая визуализация основывается на представлении изображения на экране или бумаге в виде совокупности отдельных точек (пикселов). Вместе пиксели образуют растр. Каждый пиксель может иметь свой цвет. Совокупность пикселов различного цвета образует изображение. В зависимости от расположения пикселов в пространстве различают квадратный, прямоугольный, гексагональный или иные типы растра. Для описания расположения пикселов используют разнообразные системы координат. Общим для всех таких систем является то, что координаты пикселов образуют дискретный ряд значений (необязательно целые числа). Часто используется система целых координат — номеров пикселов с (0,0) в левом верхнем углу.

Основные характеристики растра.

Разрешающая способность. Она характеризует расстояние между соседними пикселями (рис. 3). Разрешающую способность измеряют количеством пикселов на единицу длины. Наиболее популярной единицей измерения является dpi (dots per inch) — количество пикселов в одном дюйме длины (2.54 см). Не следует отождествлять шаг с размерами пикселов — размер пикселов может быть равен шагу, а может быть как меньше, так и больше, чем шаг.

Размер растра обычно измеряется количеством пикселов по горизонтали и вертикали.

Рисунок 3: Растр

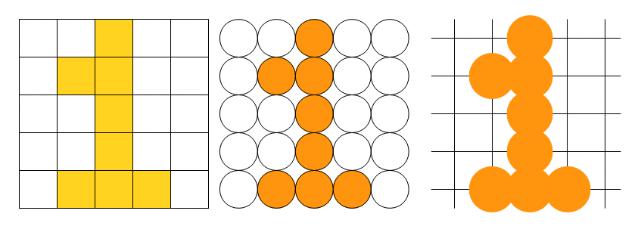
Форма пикселов растра определяется особенностями устройства графического вывода (рис. 4). Например, пиксели могут иметь форму прямоугольника или квадрата, которые по размерам равны шагу растра; пиксели круглой формы, которые по размерам могут и не равняться шагу растра.

Количество цветов (глубина цвета) — также одна из важнейших характеристик растра. Количество цветов является важной характеристикой для любого изображения, а не только растрового.

-9-

Компьютерная графика.

Рисунок 4: Примеры показа одного изображения ра различных растрах

Достоинства.

•Растровая графика позволяет создать (воспроизвести) практически любой рисунок, вне зависимости от сложности.

•Распространённость - растровая графика используется сейчас практически везде: от маленьких значков до плакатов.

•Высокая скорость обработки сложных изображений, если не нужно масштабирование.

•Растровое представление изображения естественно для большинства устройств ввода-вывода графической информации, таких как мониторы (за исключением векторных), матричные и струйные принтеры, цифровые фотоаппараты, сканеры и т.д.

Недостатки.

•Большой размер файлов с простыми изображениями.

•Невозможность идеального масштабирования.

•Невозможность вывода на печать на плоттер.

Векторная визуализация.

Векторная визуализация основывается на формировании изображения на экране или бумаге рисованием линий (векторов) — прямых или кривых. Совокупность типов линий (графических примитивов), которые используются как базовые для векторной визуализации, зависит от определенного устройства.

Способ хранения информации.

Рассмотрим, к примеру, такой графический примитив, как окружность радиуса r. Для её построения необходимо и достаточно следующих исходных данных:

•координаты центра окружности;

•значение радиуса r;

•цвет заполнения (если окружность не прозрачная);

•цвет и толщина контура (в случае наличия контура).

Достоинства.

•Размер, занимаемый описательной частью, не зависит от реальной величины объекта, что позволяет, используя минимальное количество информации, описать сколько угодно большой объект файлом минимального размера.

-10-

Компьютерная графика.

•В связи с тем, что информация об объекте хранится в описательной форме, можно бесконечно увеличить графический примитив, например, дугу окружности, и она останется гладкой

•Параметры объектов хранятся и могут быть легко изменены. Также это означает что перемещение, масштабирование, вращение, заполнение и т.д. не ухудшает качества рисунка.

•При увеличении или уменьшении объектов толщина линий может быть задана постоянной величиной, независимо от реального контура.

Недостатки.

•Не каждый объект может быть легко изображен в векторном виде — для подобного оригинальному изображению может потребоваться очень большое количество объектов и их сложности, что негативно влияет на количество памяти, занимаемой изображением, и на время для его отображения (отрисовки).

•Перевод векторной графики в растр достаточно прост. Но обратного пути, как правило, нет — трассировка растра, при том что требует значительных вычислительных мощностей и времени, не всегда обеспечивает высокое качество векторного рисунка.

-11-