
- •Введение.
- •Цели, задачи и структура курса.
- •Предмет компьютерной графики.
- •Сферы применения компьютерной графики.
- •Отображение информации.
- •Проектирование.
- •Моделирование.
- •Интерфейс пользователя.
- •Графическая система.
- •Объект и наблюдатель.
- •Визуализация изображений.
- •Растровая визуализация.
- •Векторная визуализация.
- •Цвет
- •Свет и изображение.
- •Глаз человека.
- •Характеристики цвета.
- •Цветовые модели.
- •Глубина цвета
- •Палитра
- •Координаты.
- •Прямоугольная система координат на плоскости.
- •Прямоугольная система координат в 3-x мерном пространстве.
- •Прямоугольная система координат в n-мерном пространстве.
- •Полярная система координат.
- •Графическое представление.
- •Трёхмерное расширение.
- •Цилиндрическая система координат.
- •Сферическая система координат.
- •Координаты в матричном виде.
- •Произведение матриц.
- •Преобразование координат.
- •Аффинные преобразования координат.
- •Аффинные преобразования координат на плоскости.
- •Однородные координаты.
- •Аффинные преобразования координат в трехмерном пространстве.
- •Преобразования объектов.
- •Аффинные преобразования объектов на плоскости.
- •Трехмерные аффинные преобразования объектов.
- •Композиция преобразований.
- •Эффективность преобразований.
- •Базовые растровые алгоритмы.
- •Связность.
- •Алгоритмы вывода прямой линии
- •Прямое вычисление координат.
- •Алгоритм Брезенхэма.
- •Алгоритм вывода окружности.
- •Алгоритм Брезенхэма построения окружности.
- •Растеризация многоугольника.
- •Алгоритм со списком реберных пересечений.
- •Алгоритм заполнения со списком активных ребер.
- •Заливка с затравкой.
- •Алгоритмы отсечения.
- •Отсечение отрезков.
- •Алгоритм Коэна-Сазерленда.
- •FC-алгоритм.
- •Алгоритм Лианга-Барски.
- •Двумерный алгоритм Кируса — Бека
- •Проверка выпуклости многоугольника и определение нормалей
- •Алгоритм с использованием векторных произведений
- •Разбиение не выпуклых многоугольников
- •Отсечение многоугольника
- •Алгоритм Сазерленда-Ходгмана
- •Простой алгоритм отсечения многоугольника
- •Алгоритм отсечения многоугольника Вейлера-Азертона
- •Удаление невидимых линий и поверхностей.
- •Алгоритм удаления поверхностей с Z-буфером.
- •Алгоритм разбиения области Варнока.
- •Алгоритм трассировки лучей.
Компьютерная графика.
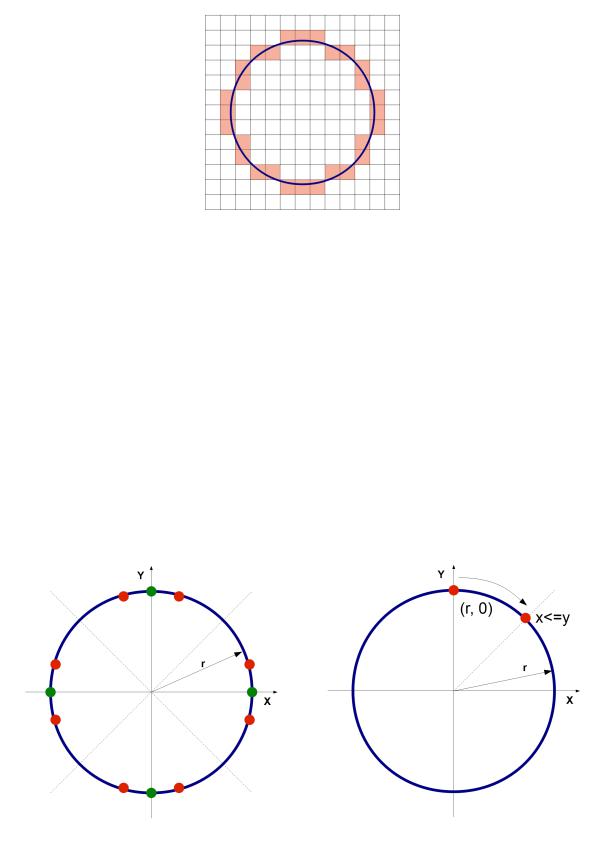
Алгоритм вывода окружности.
Рисунок 22: Растеризация окружности.
Для вывода окружности можно использовать соотношение между координатами X и Y для точек круга X2 + Y2 = R2 и построить алгоритм прямого вычисления координат. Однако тогда необходимо вычислять квадратный корень, а это выполняется медленно.
Алгоритм Брезенхэма построения окружности.
Окружность строится так же на принципе центральной точки. Для начала необходимо поставить четыре точки на пересечении осей координат и окружности. Далее воспользуемся свойством симметричности окружности, за начальные значения возьмем x = 0, y = r , а за критерий выхода из цикла x <= y. Это означает, как только построим восьмую часть окружности цикл завершится. Так же на каждой итерации цикла мы будем устанавливать не одну, а сразу восемь симметрично расположенных точек.
Рисунок 23: Алгоритм построения окружности.
-38-
Компьютерная графика.
Теперь необходимо рассмотреть принцип выбора закрашиваемого пикселя. Для этого нам необходимо уравнение окружности:
x2 + y2=r2 ,
получаем функцию:
f(x , y )=x2 + y2−r2 .
Вфункцию f(x,y) мы можем подставить координаты любой точки и проверить, находится точка внутри окружности или снаружи. Отметим, считается что центр окружности находится в центре координат (cx = 0, cy = 0).
{f (x , y)>0 f (x , y )=0 f (x , y)<0
точка( x , y)вне окружности , точка( x , y)на окружности , точка( x , y)внутри окружности.
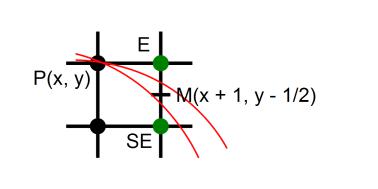
Далее по известному алгоритму, подставляем центральную точку и выбираем направление.
Рисунок 24: Алгоритм Брезенхэма.
Алгоритм на языке C/C++:
int x = 0; float y = r; float f;
SetPixel(cx, cy + r);
SetPixel(cx, cy - r);
SetPixel(cx + r, cy);
SetPixel(cx - r, cy);
while(x <= y)
{
f = (x + 1) * (x + 1) + (y - 0.5) * (y - 0.5) - r * r;
if(f > 0)
{
y = y - 1;
}
x = x + 1;
-39-
Компьютерная графика.
SetPixel(cx + x, cy + y);
SetPixel(cx + x, cy - y);
SetPixel(cx - x, cy + y);
SetPixel(cx - x, cy - y);
SetPixel(cx + y, cy + x);
SetPixel(cx + y, cy — x);
}
Данный алгоритм наделен некоторыми недостатками, а точнее вещественной арифметикой и вычислениями на каждой итерации цикла. Для избавления от этих недостатков необходимо рассмотреть две итерации цикла и внести некоторые изменения в алгоритм.
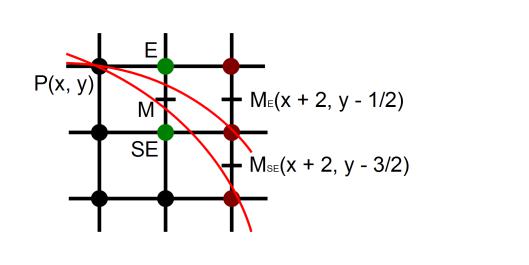
На 1-й итерации цикла мы рассматриваем точку M(x+1, y-1/2), на следующей итерации нам необходимо рассматривать точку ME(x+2, y-1/2), либо точку MSE(x+2, y-3/2). Запишем значения функции f(x,y) на этих итерациях:
f(M )= f (x+1, y−1 /2)=( x+1)2+( y−1 /2)2−r2=x2+2x+1+ y2−y+1/ 4−r2 ,
f(M E )= f ( x+2, y−1 /2)=( x+2)2+( y−1/ 2)2−r2=x2+4x+4 + y2− y+1/ 4−r2= f ( M )+2x+3,
f(M SE )= f ( x+2, y−3/2 )=(x+2)2+( y−3/2 )2−r2=x2 +4x+4+ y2−3y+9 /4−r2= f (M )+2x−2y+5.
Рисунок 25: Алгоритм Брезенхэма.
Приращения найдены, осталось найти значение функции в самой первой точке
(x1,y1):
f (M 0)= f (1, r−1 /2)=12 +(r−1/2)2−r 2=1+r2−r−1 /4−r2 =5/4−r.
Если посмотреть внимательнее на приращения, то можно заметить что приращения целочисленные в обоих случаях (2x + 3) и (2x – 2y + 5), а также начальное значение f(M0) – это целое число сдвинутое на одну четверть. Это означает, что мы можем отказаться от ¼ в начальных значениях f(M0), т.к. это никак не повлияет на сравнение с нулем:
f (M 0)=1−r.
-40-
Компьютерная графика.
Реализуем алгоритм:
int x = 0; int y = r; int f = 1 - r;
SetPixel(cx, cy + r);
SetPixel(cx, cy - r);
SetPixel(cx + r, cy);
SetPixel(cx - r, cy);
while(x <= y)
{
if(f > 0)
{
y = y - 1;
f = f + 2*(x - y) + 5;
}
else
{
f = f + 2*x + 3;
}
x = x + 1;
SetPixel(cx + x, cy + y); SetPixel(cx + x, cy - y); SetPixel(cx - x, cy + y); SetPixel(cx - x, cy - y); SetPixel(cx + y, cy + x); SetPixel(cx + y, cy - x); SetPixel(cx - y, cy + x); SetPixel(cx - y, cy - x);
}
Вышеизложенный алгоритм можно оптимизировать еще раз, т.к. в вычислении приращений используются переменные x и y, а обращения к памяти также очень затратная операция для ситуаций с ограниченными ресурсами. Мы избавимся от вычислений приращения на каждой итерации.
Рассмотрим приращения по каждому направлению E и SE (incrE = 2*x + 3, incrSE = 2*(x – y) + 5):
•если выбрана точка E, то значение x увеличивается на еденицу (incrE = incrE + 2, incrSE = incrSE + 2);
•если выбрана точка SE, то значение x увеличивается на еденицу и значение y
уменьшается на 1 (incrE = incrE + 2, incrSE = incrSE + 4). Начальные значения incrE = 3, incrSE = 5 — 2*r.
Алгоритм с оптимизацией:
int x = 0; int y = r; int f = 1 - r; int incrE = 3;
int incrSE = 5 - 2 * r;
-41-
