
- •Введение.
- •Цели, задачи и структура курса.
- •Предмет компьютерной графики.
- •Сферы применения компьютерной графики.
- •Отображение информации.
- •Проектирование.
- •Моделирование.
- •Интерфейс пользователя.
- •Графическая система.
- •Объект и наблюдатель.
- •Визуализация изображений.
- •Растровая визуализация.
- •Векторная визуализация.
- •Цвет
- •Свет и изображение.
- •Глаз человека.
- •Характеристики цвета.
- •Цветовые модели.
- •Глубина цвета
- •Палитра
- •Координаты.
- •Прямоугольная система координат на плоскости.
- •Прямоугольная система координат в 3-x мерном пространстве.
- •Прямоугольная система координат в n-мерном пространстве.
- •Полярная система координат.
- •Графическое представление.
- •Трёхмерное расширение.
- •Цилиндрическая система координат.
- •Сферическая система координат.
- •Координаты в матричном виде.
- •Произведение матриц.
- •Преобразование координат.
- •Аффинные преобразования координат.
- •Аффинные преобразования координат на плоскости.
- •Однородные координаты.
- •Аффинные преобразования координат в трехмерном пространстве.
- •Преобразования объектов.
- •Аффинные преобразования объектов на плоскости.
- •Трехмерные аффинные преобразования объектов.
- •Композиция преобразований.
- •Эффективность преобразований.
- •Базовые растровые алгоритмы.
- •Связность.
- •Алгоритмы вывода прямой линии
- •Прямое вычисление координат.
- •Алгоритм Брезенхэма.
- •Алгоритм вывода окружности.
- •Алгоритм Брезенхэма построения окружности.
- •Растеризация многоугольника.
- •Алгоритм со списком реберных пересечений.
- •Алгоритм заполнения со списком активных ребер.
- •Заливка с затравкой.
- •Алгоритмы отсечения.
- •Отсечение отрезков.
- •Алгоритм Коэна-Сазерленда.
- •FC-алгоритм.
- •Алгоритм Лианга-Барски.
- •Двумерный алгоритм Кируса — Бека
- •Проверка выпуклости многоугольника и определение нормалей
- •Алгоритм с использованием векторных произведений
- •Разбиение не выпуклых многоугольников
- •Отсечение многоугольника
- •Алгоритм Сазерленда-Ходгмана
- •Простой алгоритм отсечения многоугольника
- •Алгоритм отсечения многоугольника Вейлера-Азертона
- •Удаление невидимых линий и поверхностей.
- •Алгоритм удаления поверхностей с Z-буфером.
- •Алгоритм разбиения области Варнока.
- •Алгоритм трассировки лучей.
Компьютерная графика.
2.Многоугольник поворачивается против часовой стрелки для совмещения (i + 1)-й вершины с положительной полуосью X. Вектор внутреннего перпендикуляра к ребру, образованному вершинами i-й и (i + 1)-й, вычисляется поворотом ребра на -90° против часовой стрелки.
3.Анализируется знак Y-координаты (i + 2)-й вершины.
Если Yi+2 >= 0, то в (i + 1)-й вершине выпуклость.
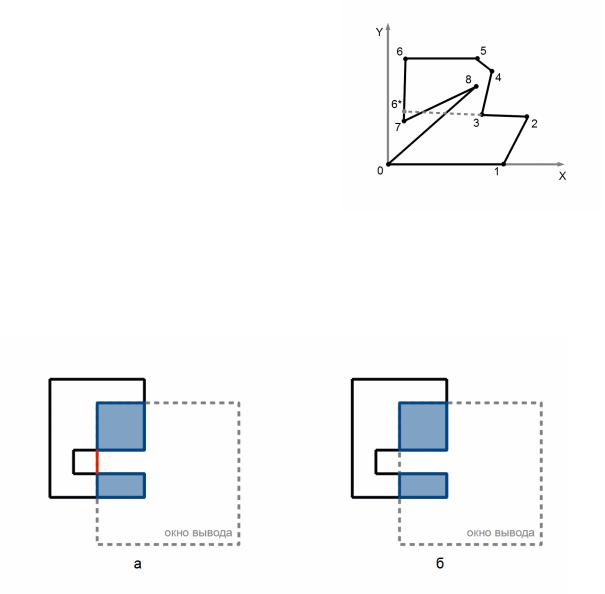
Если Yi+2 < 0, то в (i + 1)-й вершине не выпуклость и многоугольник разрезается на два вдоль положительной полуоси X. Для этого вычисляется пересечение положительной полуоси X с первой из сторон. Формируются два новых многоугольника: первый многоугольник - вершины с (i + 1)-й до точки пересечения (рис. 45 б; вершины 3, 4, 5, 6, 7, 8, 8*); второй многоугольник - все остальные вершины (рис. 45 б; вершины 0, 1, 2, 3, 8*).
Так как вновь полученные многоугольники могут в свою очередь оказаться вогнутыми, алгоритм применяется к ним, пока все многоугольники не станут выпуклыми.
Повторное применение алгоритма к многоугольнику, образованному вершинами 2, 3, 4, 5, 6, 7, 7*, показано на рис. 45 в. Данный алгоритм не обеспечивает минимальность числа вновь полученных выпуклых многоугольников и некорректно работает если имеется самопересечение сторон (рис. 46).
Отсечение многоугольника
Рисунок 46: Многоугольник с самопересечением сторон
Многоугольники особенно важны в растровой графике как средство задания поверхностей. Будем называть многоугольник, используемый в качестве окна отсечения, отсекателем, а многоугольник, который отсекается, - отсекаемым.
Рисунок 47: Отсечение окном многоугольника (а - некорректное отсечение, б - корректное отсечение)
Алгоритм отсечения многоугольника должен в результате отсечения давать один или несколько замкнутых многоугольников (рис. 47). При этом могут быть добавлены новые ребра, а имеющиеся или сохранены или разделены или даже отброшены.
-62-
Компьютерная графика.
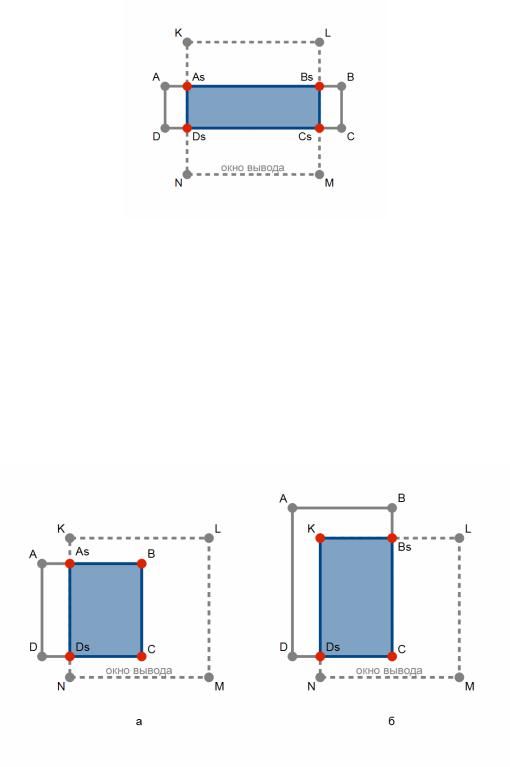
Существенно, чтобы границы окна, которые не ограничивают видимую часть отсекаемого многоугольника, не входили в состав результата отсечения. Если это не выполняется, то возможна излишняя закраска границ окна (рис. 47).
Рисунок 48: Отсечение окном многоугольника (результатом отсечения являются отрезки AsBs и CsDs)
В принципе эту задачу можно решить с использованием рассмотренных ранее алгоритмов отсечения линий, если рассматривать многоугольник просто как набор векторов, а не как сплошные закрашиваемые области. При этом вектора, составляющие многоугольник, просто последовательно отсекаются сторонами окна (рис. 48).
Если же в результате отсечения должен быть получен замкнутый многоугольник, то формируется вектор, соединяющий последнюю видимую точку с точкой пересечения с окном (рис. 49 а). Проблема возникает при окружении отсекаемым многоугольником угла окна (рис. 49 б).
Рисунок 49: Отсечение сплошного многоугольника окном (а - простой случай, б - сложный случай)
Далее мы рассмотрим три алгоритма корректно решающие задачу отсечения сплошного многоугольника. Первые два алгоритма быстро работают, но генерируют
-63-
Компьютерная графика.
лишние ребра, как это продемонстрировано на рис. 49 б. Последний алгоритм свободен от данного недостатка.
В общем, при отсечении многоугольников возникают два типа задач - отображение части изображения попавшей в окно и наоборот, отображение изображения, находящегося вне окна. Все здесь рассматриваемые алгоритмы могут использоваться в обоих случаях.
Алгоритм Сазерленда-Ходгмана
Простой метод решения проблемы охвата отсекаемым многоугольником вершины окна предлагается в алгоритме Сазерленда-Хогдмана, когда весь многоугольник последовательно отсекается каждой границей окна, как это показано на рис. 50.
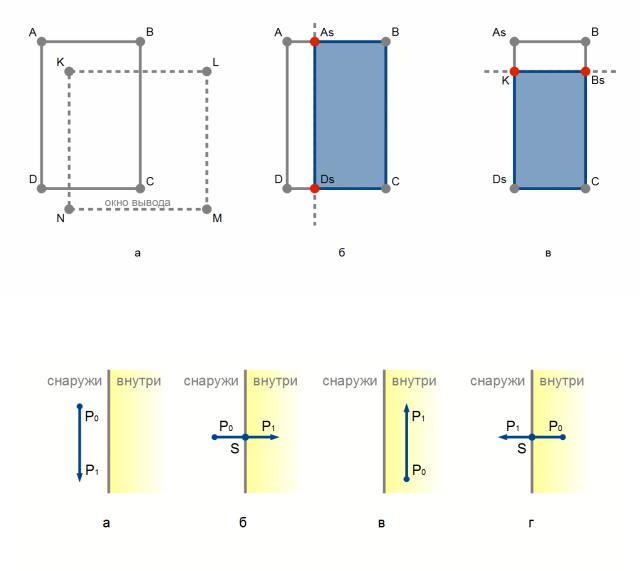
Рисунок 50: Последовательное отсечение многоугольника сторонами окна (а — исходное изображение, б — отсечение левой стороной окна, в — отсечение верхней гранцей окна)
Рисунок 51: Относительное расположение отрезка и границы окна (а — отрезок находится на внешней стороне ребра отсечения, б — отрезок пересекает ребро отсечения и направлен с внешней стороны во внутреннюю, в - отрезок находится на внутренней стороне ребра отсечения, г - отрезок пересекает ребро отсечения и направлен с внутренней стороны на внешнюю)
При отсечении ребра, соединяющего очередную пару вершин P0 и P1, возможны 4
-64-
Компьютерная графика.
случая взаимного расположения:
1.ребро на внешней стороне границы (рис. 51 а), в результат ничего не добавляется;
2.ребро входит снаружи в окно (рис. 51 б), в результат добавляется точка пересечения S и конечная точка ребра P1;
3.ребро на внутренней стороне границы (рис. 51 в), в результат добавляется конечная точка ребра P1;
4.ребро выходит из окна наружу (рис. 51 г) в результат добавляется точка пересечения S.
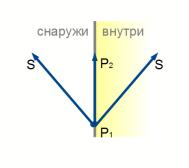
Для определения взаимного расположения и направленности используется векторное произведение вектора P1P2, проведенного из начальной в конечную точку текущего ребра окна, на вектор P1S из начальной точки текущего ребра окна в очередную вершину S многоугольника (рис. 52).
Рисунок 52: Определение взаимного расположения окна и вершины
Если P1P2 × P1S < 0, то поворот от P1P2 к P1S по часовой стрелке, т.е. точка S внутри окна.
Если P1P2 × P1S > 0, то поворот от P1P2 к P1S против часовой стрелки, т.е. точка S вне окна.
В алгоритме Сазерленда-Ходгмана в результат могут заноситься границы окна, даже если они и не ограничивают видимую часть отсеченного многоугольника. Это можно устранить дополнительным анализом, либо используя более сложный алгоритм отсечения.
Простой алгоритм отсечения многоугольника
В данном разделе рассматривается простой алгоритм отсечения, который подобно алгоритму Сазерленда-Ходгмана может генерировать лишние стороны для отсеченного многоугольника, проходящие вдоль ребра окна отсечения. Но этот алгоритм несколько более быстрый и использует те же подпрограммы обработки многоугольного окна отсечения, что и алгоритм Кируса-Бека.
Многоугольник отсекается одним ребром выпуклого окна отсечения. В результате такого отсечения формируется новый многоугольник, который затем отсекается следующим ребром и т.д., пока не будет выполнено отсечение последним ребром окна.
Основная здесь процедура - процедура отсечения отдельным ребром, определяющая взаимное расположение очередной стороны многоугольника и ребра
-65-
Компьютерная графика.
отсекателя и генерирующая соответствующие выходные данные.
Возможны 9 различных случаев расположения ребра окна и отсекаемой стороны, показанных на рис. 53 - 55.
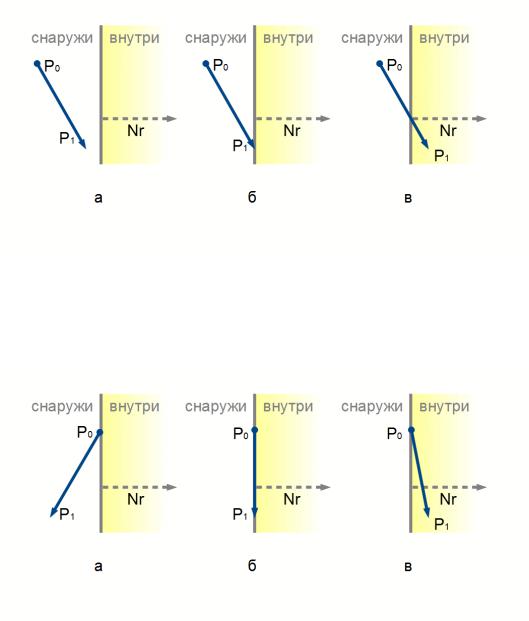
Рисунок 53: Расположение ребра окна и отсекаемого отрезка (а - начальная и конечная точки вне окна отсечения, б - начальная точка вне окна, конечная на границе окна, в - начальная точка вне окна, конечная внутри окна отсечения)
На них P0 и P1 - начальная и конечная точки отсекаемой стороны многоугольника, соответственно; Nr - нормаль к ребру окна отсечения, направленная внутрь окна.
Рисунок 54: Расположение ребра окна и отсекаемого отрезка (а - начальная точка на границе окна, конечная точка вне окна, б - начальная и конечная точки на границе окна, в - начальная точка на границе окна, конечная внутри окна отсечения)
Из этих рисунков очевидны правила генерации выходных данных, зависящие от варианта взаимного расположения:
1.Нет выходных данных (рис. 53 а).
2.В выходные данные заносится конечная точка (рис. 53 б).
3.Рассчитывается пересечение и в выходные данные заносятся точка пересечения и конечная точка (рис. 53 в).
4.Нет выходных данных (рис. 54 а).
5.В выходные данные заносится конечная точка (рис. 54 б).
6.В выходные данные заносится конечная точка (рис. 54 в).
-66-
Компьютерная графика.
7.Рассчитывается пересечение и в выходные данные заносится только точка пересечения (рис. 55 а).
8.В выходные данные заносится конечная точка (рис. 55 б).
9.В выходные данные заносится конечная точка (рис. 55 в).
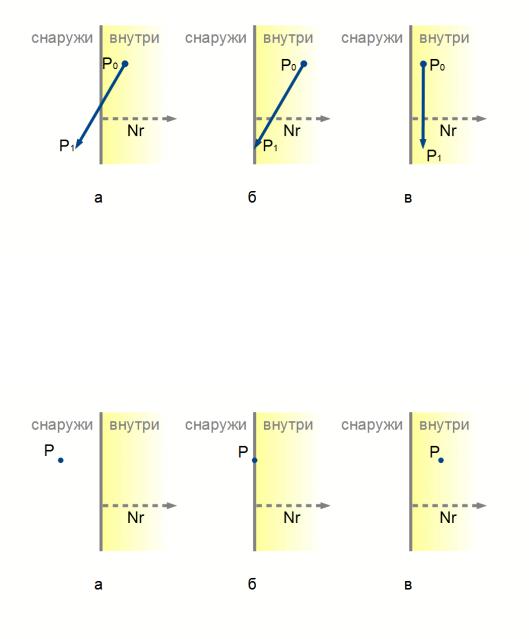
Рисунок 55: Расположение ребра окна и отсекаемого отрезка (а - начальная точка внутри окна отсечения, конечная точка вне окна, б - начальная точка внутри окна отсечения, конечная точки на границе окна, в - начальная и конечная точки внутри окна отсечения)
Для определения взаимного расположения, подобно алгоритму отсечения КирусаБека, используется скалярное произведение Q вектора нормали на вектор, проведенный из начала ребра в анализируемую точку (рис. 56).
Рисунок 56: Анализ расположения точки относительно ребра окна отсечения (а - точка снаружи, б - точка на границе ребра, в - точка внутри)
Таким образом, для определения взаимного расположения начальной P0 и конечной P1 точек отсекаемой стороны и ребра отсечения с вектором его начала R, надо вычислить:
Qn = ( P0 |
– R ) ∙ Nr |
(26) |
|
Qk = ( P1 – R ) ∙ Nr |
|||
|
|||
Расчет пересечения, если он требуется, производится аналогично алгоритму Кируса-
-67-
