Компьютерная графика.

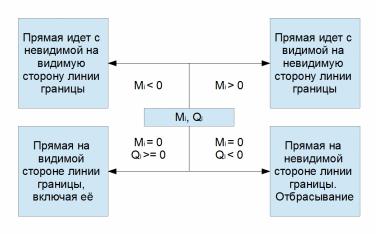
отрезка. В этом случае определяется максимальное значение из всех получаемых решений. Оно даст значение параметра t0 для начальной точки отсеченного отрезка. Если текущее полученное значение t0 окажется больше, чем t1, то отрезок отбрасывается, так как нарушено условие t0 <= t1.

На заключительном этапе алгоритма значения t0 и t1 используются для вычисления координат точек пересечения отрезка с окном. При этом, если t0 = 0, то начальная точка осталась P0 и вычисления не нужны. Аналогично, если t1 = 1, то конечная точка осталась P1 и вычисления также не нужны.

Все эти случаи пояснены на блок-схеме, представленной на рис. 43.

Рисунок 43: Блок-схема алгоритма Кируса-Бека

Вычисления значений параметров t0 и t1 выполняются в соответствии с выражениями (25).

Проверка выпуклости многоугольника и определение нормалей

Как видно из описания, алгоритм Кируса-Бека отсекает только по выпуклому окну. Кроме этого требуются значения внутренних нормалей к сторонам окна. Естественно выполнить эти вычисления в момент задания окна, так как следует ожидать, что одним окном будет отсекаться достаточно много отрезков.

Алгоритм с использованием векторных произведений

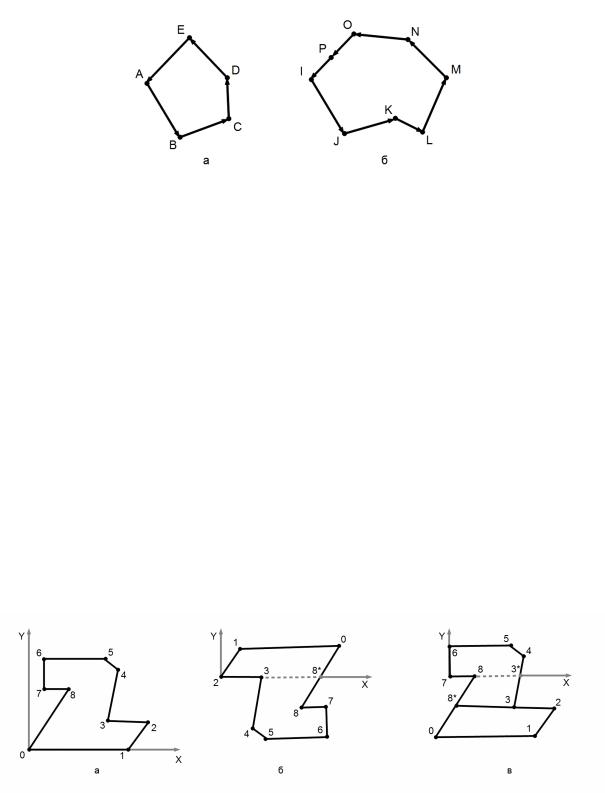
Проверка на выпуклость может производиться анализом знаков векторных произведений (произведение длин векторов умноженный на синус угла между векторами) смежных ребер (рис. 44).

-60-

Компьютерная графика.

Рисунок 44: Проверка выпуклости и определение нормалей (а - выпуклый многоугольник, б - не выпуклый многоугольник)

Далее определяем:

•Если знак векторного произведения равен 0, то вершина вырождена, т.е. смежные ребра лежат на одной прямой (рис. 44 б, вершина P).

•Если все знаки равны 0, то многоугольник отсечения вырождается в отрезок.

•Если же векторные произведения имеют разные знаки, то многоугольник отсечения не выпуклый (рис. 44 б).

•Если все знаки неотрицательные, то многоугольник выпуклый, причем обход вершин выполняется против часовой стрелки (рис. 44 а), т.е. внутренние нормали ориентированы влево от контура. Следовательно вектор внутреннего перпендикуляра к стороне может быть получен поворотом ребра на +90°.

•Если все знаки не положительные, то многоугольник выпуклый, причем обход вершин выполняется по часовой стрелке, т.е. внутренние нормали ориентированы вправо от контура. Следовательно вектор внутреннего перпендикуляра к стороне может быть получен поворотом ребра на -90°.

Разбиение не выпуклых многоугольников

Одновременное проведение операций проверки на выпуклость и разбиение простого не выпуклого многоугольника на выпуклые обеспечивается методом переноса и поворотов окна.

Рисунок 45: Проверка выпуклости и разбиение многоугольника (а - исходное окно, б — вогнутость после 3-й вершины, в — вогнутость после 8-й вершины)

Алгоритм метода при обходе вершин многоугольника против часовой стрелки состоит

вследующем:

1.Для каждой i-й вершины многоугольник сдвигается для переноса упомянутой вершины в начало координат.

-61-