Компьютерная графика.
пересечения вначале сравнивается с C0. Если C0 далее вдоль линии, чем точка пересечения, тогда C0 (и, следовательно C0C1) находится на невидимой стороне линии границы, т.е. отрезок должен быть отброшен. В противном случае точка пересечения сравнивается с C1 и, если C1 далее вдоль линии, тогда C1 перемещается назад к точке пересечения.
Наконец, если удлиненная линия параллельна граничной линии и она на невидимой стороне, то отрезок отбрасывается. В конце алгоритма, если отрезок не отброшен, тогда C0 и C1 используются как конечные точки видимой части отрезка.
Двумерный алгоритм Кируса — Бека
Все рассмотренные выше алгоритмы проводили отсечение по прямоугольному окну, стороны которого параллельны осям координат. Это, конечно, наиболее частый случай отсечения. Однако, во многих случаях требуется отсечение по произвольному многоугольнику, например, в алгоритмах удаления невидимых частей сцены. В этом случае наиболее удобно использование параметрического представления линий, не зависящего от выбора системы координат.
Из предыдущего пункта ясно, что для выполнения отсечения в параметрическом представлении необходимо иметь способ определения ориентации удлиненной линии, содержащей отсекаемый отрезок, относительно линии границы - с внешней стороны на внутреннюю или с внутренней на внешнюю, а также иметь способ определения расположения точки, принадлежащей отрезку, относительно окна - вне, на границе, внутри.
Для этих целей в алгоритме Кируса-Бека, реализующем отсечение произвольным выпуклым многоугольником, используется вектор внутренней нормали к ребру окна. Внутренней нормалью NB в точке А к стороне окна называется нормаль, направленная в сторону области, задаваемой окном отсечения.
Рассмотрим основные идеи алгоритма Кируса-Бека.
Так как многоугольник предполагается выпуклым, то может быть только две точки пересечения отрезка с окном. Поэтому надо найти два значения параметра t, соответствующие начальной и конечной точкам видимой части отрезка.
Пусть Ni - внутренняя нормаль к i-й граничной линии окна, а M = P1 – P0 - вектор, определяющий ориентацию отсекаемого отрезка, тогда ориентация отрезка относительно i-й стороны окна определяется знаком скалярного произведения Mi = Ni ∙ M, равного произведению длин векторов на косинус наименьшего угла, требуемого для поворота вектора Ni до совпадения по направлению с вектором M:
Mi = Ni ∙ M = Ni ∙ (P1 – P0) |
(16) |
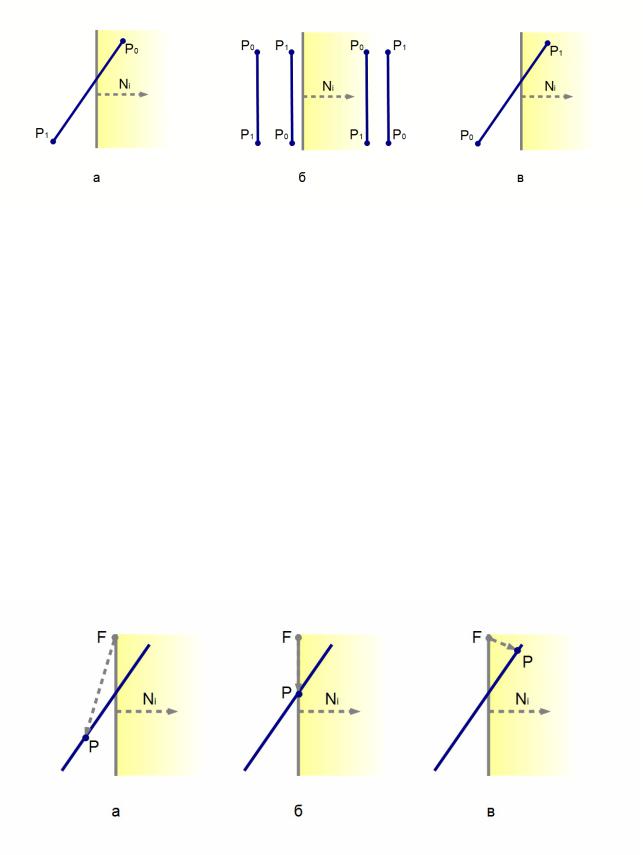
При Mi < 0 отсекаемый отрезок направлен с внутренней на внешнюю стороны i-й граничной линии окна (рис. 41 а)
При Mi = 0 отсекаемый отрезок вырожден в точку, либо отрезок (17) параллелен i-й граничной линии окна (рис. 41 б)
При Mi > 0 отсекаемый отрезок направлен с внешней на внутреннюю сторону i-й граничной линии окна (рис. 41 в)
-57-
Компьютерная графика.
Рисунок 41: Ориентация отсекаемого отрезка относительно окна (a - отрезок направлен изнутри наружу, б - отрезок параллелен границе, в - отрезок направлен снаружи внутрь)
Для определения расположения точки относительно окна вспомним параметрическое представление отсекаемого отрезка:
M(t) = P0 + (P1 - P0) · t; где: 0 <= t <= 1 |
(18) |
Рассмотрим теперь скалярное произведение внутренней нормали Ni к i-й границе на вектор Q(t) = M(t) - Fi, начинающийся в начальной точке ребра окна и заканчивающийся в некоторой точке M(t) удлиненной линии.
Qi = Ni · Q = Ni · [M(t) — Fi]; для i = 1, 2, 3... |
(19) |
Теперь имеем:
При Qi < 0 точка M(t) лежит с внешней стороны границы (рис. 42 а);
При Qi = 0 точка M(t) лежит на самой границе (рис. 42 б); (20) При Qi > 0 точка M(t) лежит с внутренней стороны границы (рис. 42 в).
Рисунок 42: Расположение точки относительно окна (а - точка вне окна, б - точка находится на границе окна, в - точка внутри окна)
-58-
Компьютерная графика.
Подставляя в (19) параметрическое представление (18), получим условие пересечения отрезка с границей окна:
Ni · [ P0 + (P1 - P0) · t - Fi ] = 0 |
(21) |
Раскрывая скобки, получим:
Ni · [ P0 - Fi ] + Ni · [ P1 — P0 ] · t ] = 0 |
(22) |
Используя (16) и (19) перепишем (21):
(Ni · M) · t + Ni · Q = Mi · t + Qi |
(23) |
Разрешая (22) относительно t, получим:
t = - Qi / Mi = - (Ni · Q) / (Ni · M); при Mi <> 0, i = 1, 2, 3 ... |
(24) |
Это уравнение и используется для вычисления значений параметров, соответствующих начальной и конечной точкам видимой части отрезка.
Как следует из (17), Mi равно нулю если отрезок либо вырожден в точку, либо параллелен границе. В этом случае следует проанализировать знак Qi и принять или не принять решение об отбрасывании отрезка целиком в соответствии с условиями (17).
Если же Mi не равно 0, то уравнение (24) используется для вычисления значений параметров t, соответствующих точкам пересечений удлиненной линии с линиями границ.
Алгоритм построен следующим образом:
Искомые значения параметров t0 и t1 точек пересечения инициализируются значениями 0 и 1, соответствующими началу и концу отсекаемого отрезка.
Затем в цикле для каждой i-й стороны окна отсечения вычисляются значения скалярных произведений, входящих в (23).
Если очередное Mi равно 0, то отсекаемый отрезок либо вырожден в точку, либо параллелен i-й стороне окна. При этом достаточно проанализировать знак Qi. Если Qi < 0, то отрезок вне окна и отсечение закончено иначе рассматривается следующая сторона окна.
Если же Mi не равно 0, то по (24) можно вычислить значение параметра t для точки пересечения отсекаемого отрезка с i-й границей. Так как отрезок P0P1 соответствует диапазону 0 <= t <= 1, то все решения, выходящие за данный диапазон следует отбросить. Выбор оставшихся решений определяется знаком Mi.
Если Mi < 0, т.е. удлиненная линия направлена с внутренней на внешнюю стороны граничной линии, то ищутся значения параметра для конечной точки видимой части отрезка. В этом случае определяется минимальное значение из всех получаемых решений. Оно даст значение параметра t1 для конечной точки отсеченного отрезка. Если текущее полученное значение t1 окажется меньше, чем t0, то отрезок отбрасывается, так как нарушено условие t0 <= t1.
Если же Mi > 0, т.е. удлиненная линия направлена с внешней на внутреннюю стороны граничной линии, то ищутся значения параметра для начальной точки видимой части
-59-