Компьютерная графика.

SetPixel(cx, cy + r);

SetPixel(cx, cy - r);

SetPixel(cx + r, cy);

SetPixel(cx - r, cy);

while(x <= y)

{

if(f > 0)

{

y = y - 1;

f = f + incrSE; incrSE = incrSE + 4;

}

else

{

f = f + incrE; incrSE = incrSE + 2;

}

x = x + 1;

incrE = incrE + 2;

SetPixel(cx + x, cy + y); SetPixel(cx + x, cy - y); SetPixel(cx - x, cy + y); SetPixel(cx - x, cy - y); SetPixel(cx + y, cy + x); SetPixel(cx + y, cy - x); SetPixel(cx - y, cy + x); SetPixel(cx - y, cy - x);

}

Растеризация многоугольника.

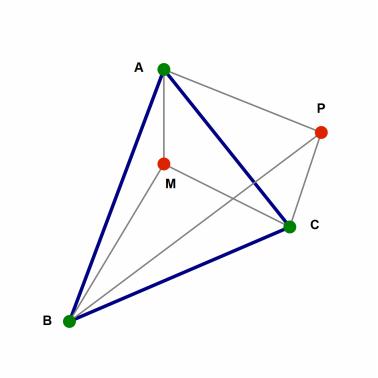
Различают два вида многоугольников: закрашенный и не закрашенный. Для постройки не закрашенного многоугольника применяется последовательный вывод отрезков от одной вершины до другой. С закрашенным многоугольником дело обстоит сложнее. Необходимо определить цвет каких пикселей менять. Можно перебором определить принадлежит ли пиксель многоугольнику и если принадлежит менять его цвет, иначе оставлять нетронутым. Рассмотрим многоугольник ABC и две точки M и P (рис. 26).

-42-

Компьютерная графика.

Рисунок 26: Принадлежность точки многоугольнику.

Сумма углов AMB, AMC и BMC равна 360 градусам, а сумма углов APB, APC и BPC меньше 360 градусов. То есть сумма углов с вершиной в точке равна 360 градусов, если точка находится внутри многоугольника, и меньше 360 градусов, если точка находится снаружи многоугольника (для выпуклого многоугольника). Такой подход очень затратен относительно ресурсов, т. к. необходимо проверить каждый пиксель на полотне. Рассмотрим другие методы.

Алгоритм со списком реберных пересечений.

Пусть задан многоугольник (P1,P2, . . . PN) и требуется растеризовать его вместе с внутренними точками. Для удобства каждое ребро многоугольника будем задавать координатами (x1, y1) и (x2, y2) его концов, так, что (y2 >= y1). Большинство алгоритмов заполнения основано на том факте, что любое горизонтальное сечение контура многоугольника состоит из четного числа точек.

Это утверждение неверно в двух случаях:

•когда секущая прямая содержит горизонтальное ребро;

•когда она содержит вершину, а оба смежных ребра лежат выше (ниже) ее.

-43-

Компьютерная графика.

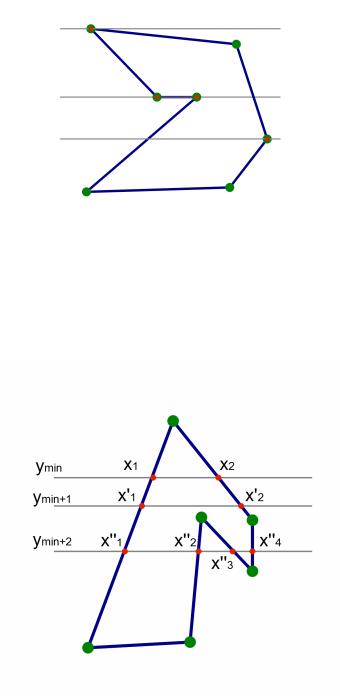
Рисунок 27: Частные случаи пересечения горизонтали с многоугольником.

Однако существуют простые способы исключить эти случаи из рассмотрения. Например при пересечении горизонталью развернутого угла можно условиться, что при такой ситуации учитывать только либо пересечение с верхним ребром, либо с нижним.

Рисунок 28: Точки пересечения горизонталей с многоугольником.

Алгоритм со списком реберных пересечений состоит из трех основных этапов.

•На первом этапе растеризуются все не горизонтальные ребра многоугольника.

Все точки помещаются в списки. Для каждой координаты ymin, ymin+1 . . . ymax сопоставим список x-координат всех пикселей, закрашенных при

растеризации ребер, которые находятся на горизонтали y (здесь ymin и ymax - минимальная и максимальная y-координаты пикселей в растровом изображении многоугольника).

•На втором этапе для каждого y списки упорядочиваются по возрастанию.

•На третьем этапе в каждой строке заполняются все отрезки вида [x2i-1, x2i].

-44-