Компьютерная графика.

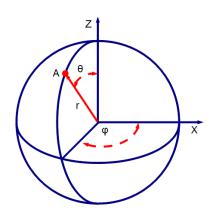
(называется зенитом или широтой, значения находятся в интервале от 0 до 180°). То есть, сферические координаты, это тройка (r, φ, θ), где r — расстояние от центра координат, φ— угол от оси x (как и в плоских полярных координатах), θ — широта.

Лучшим контекстом применения полярных координат являются случаи, тесно связанные с направлением и расстоянием от некоторого центра. Кроме того, многие физических системы — такие, которые содержат тела, движущиеся вокруг центра, либо явления, распространяющиеся из некоторого центра — гораздо проще моделировать в полярных координатах.

Полярную систему координат часто применяют в навигации, поскольку пункт назначения можно задать как расстояние и направление движения от отправной точки. Например, в авиации, для навигации применяют несколько изменённую версию полярных координат. В этой системе, обычно используемой для навигации, луч 0°

называют направлением 360, а углы отсчитываются в направлении по часовой стрелке. Направление 360 соответствует магнитному северу, а направления 90, 180, и 270 соответствуют магнитным востоку, югу и западу. Так, самолёт, летящий 5 морских миль на восток можно описать как самолёт, летящий 5 единиц в направлении 90.

Координаты в матричном виде.

Координаты точки на плоскости можно задать так называемым вектор-столбцом:

[xy]

В 3-х мерном пространстве:

[x] y z

Далее мы будем использовать матрицы для работы с координатами.

Произведение матриц.

Для двух матриц А размером (m×n) и В размером (n×р):

произведением матриц является матрица С = А×В размером (m×р):

-21-