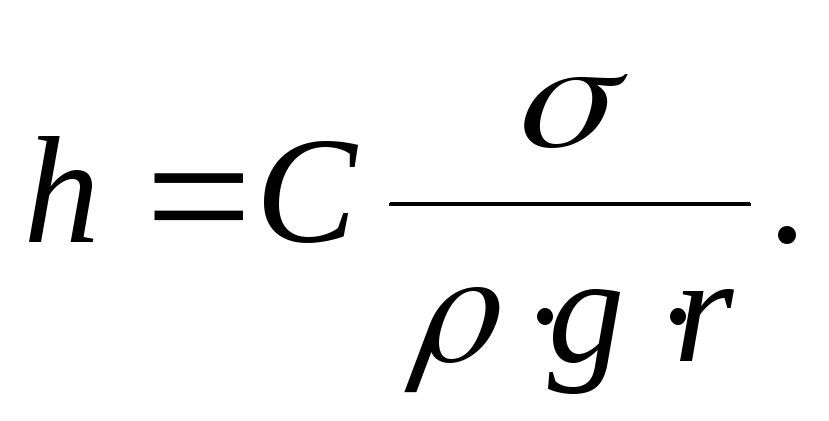1. Общий вид размерности физических величин устанавливается зависимостью ( .1).

2. Во всяком физическом законе типа

A=B ( .2)

размерности обеих частей равенства должны быть одинаковы.

В таком виде эта теорема получила название правила размерностей. В равенство типа A=B могут входить также в качестве множителей либо постоянные коэффициенты, либо безразмерные комбинации физических величин.

Очевидно, что показатели степени у любой из величин l, m, t одинаковы в левой и правой частях ( .2).

Теория размерностей без привлечения дополнительных данных, не может привести ни к каким физическим зависимостям, поскольку в ее основы не заложено никаких физических законов. Для того чтобы получить с помощью этой теории конкретные выводы, необходимо установить, между какими физическими величинами существуют количественные связи. На этот вопрос теория размерности не может дать никакого ответа. Это можно сделать только либо опытным путем, либо с помощью каких-то физических законов. Приведенные ниже примеры и задачи служат иллюстрацией сказанного. Вначале для лучшего понимания метода анализа размерностей приводятся простые примеры из механики.

Для применения метода анализа размерностей не существует теории в обычном смысле этого слова, поэтому для успешного его применения необходимо рассмотреть максимальное число примеров. Для начала решаются две задачи из механики.

Задача 1. Тело начинает свободно падать из состояния покоя. Найти вид зависимости для пути, проходимого телом.

Решение. Рассматривается падение тела, когда на него действует только сила тяжести. В действительности на него действует сила сопротивления со стороны воздуха, но в данном случае она не учитывается.

Путь, проходимый телом, прежде всего, конечно, является функцией времени. Кроме того, путь будет зависеть от ускорения свободного падения g – таким образом предложено два аргумента искомой зависимости t и g. Поэтому окончательный вид функциональной зависимости для пути

и функция f(g,t) должна иметь размерность длины, т.е.

.

Согласно первой теореме ( 1) функция f(g,t) является степенной относительно своих аргументов, т.е. имеет вид

,

где С- некоторый постоянный множитель, а α и β такие числа, что выполняется условие

. ( .3 )

Обычно следующим шагом является выражение всех входящих в правую часть ( .3) величин через основные; в данном случае это необходимо сделать для ускорения g: [g]=Lt^-2 .

Тогда из (3) следует

.

Заметим, что в правой части последнего равенства присутствует время, а в левой части его нет, поэтому в левой части представим сомножитель t⁰ (он равен единице), который ничего не изменит

.

Ясно, что если какая- либо величина находится одновременно в правой и левой частях равенстве вида (3), то показатель степени у этой величины в левой части равен показателю степени в правой части.

Поэтому при применении этого правила к последнему равенству будем иметь:

для показателя степени у L: 1=α; для показателя степени у t: 0=β-2α.

Величины α и β находятся из системы уравнений

.

Решая последнюю систему, получим:

α=1, β=2

окончательно:

.

Искомая зависимость установлена нами с точностью до некоторого безразмерного постоянного множителя, определить который с помощью данного метода невозможно (эта же зависимость, найденная более сложным образом имеет вид .

Для иллюстрации того, что первая стадия решения является самой важной и трудной, предположим, что нами принято решение о включении в число аргументов массы тела.

Тогда в правой части будет присутствовать масса в некоторой степени, а в левой она будет у нулевой степени, т.е.

,

в этом случае повторяя прежние рассуждения и решая систему уравнений найдем, что γ=0, т.е. масса в правую часть входить не должна.

После решения рассмотренной задачи возможно сделать следующее заключение.

Применение метода анализа размерностей состоит из следующих стадий:

1. Начальная стадия, наиболее трудная и ответственная- выбор необходимых аргументов х, у,…, которые являются определяющими и задание функции

z=f(x,y,…), (4)

где z- физическая величина , для которой находится зависимость от аргументов х,у,….

На этой стадии необходимо ясно представлять физическую сторону явления, свести число аргументов к минимуму (рассматривая только основные из них).

2. Правая часть (4) приводится к степенному виду.

3. Составляется система уравнений, неизвестными в которой являются показатели степени; затем эта система решается.

4. Окончательно представляется функция типа (4) и производится ее анализ с точки зрения физического смысла и различных ограничений. Намечается способ определения постоянной С опытным путем.

Замечание 3. С помощью метода анализа размерностей не удается точно определить значение постоянного безразмерного сомножителя. Его определить с помощью данного метода принципиально невозможно. Очень часто возможно измерить в опытах (или косвенно определить) все основные аргументы и искомую величину (они связаны соотношением, полученным методом анализа размерностей). Тогда становится возможным определить числовое значение ранее неизвестного коэффициента C, входящего в виде сомножителя. Часто для этого достаточно проделать всего лишь один опыт.

Замечание 4. С помощью метода анализа размерностей, как никаким другим методом, возможно быстро и просто получить зависимость, определяющую вид функции и порядок величин аргументов.

Замечание 5. В качестве сомножителя, как это было в приведенном выше примере, в любую часть (2) возможно подставить любую величину в нулевой степени.

Задача 2. Математический маятник отклонен на угол 16º и отпущен без начальной скорости. Найти вид зависимости для периода колебаний маятника.

Решение. Математический маятник представляет собой тяжелую материальную точку, подвешенную на невесомой и нерастяжимой нити, которая закреплена другим своим концом неподвижно. Для наглядного представления процесса колебаний возможно его воспроизвести, привязав к тонкой прочной нити небольшой тяжелый груз и заставив его колебаться. Достаточно нескольких опытов с разными длинами нити, чтобы убедиться – на период колебаний влияет длина маятника (причем, чем короче нить, тем период меньше). Не будем учитывать сопротивление воздуха при колебаниях.

Колебания представляют процесс перехода потенциальной энергии груза в кинетическую и обратно под действием силы тяжести, поэтому в число аргументов должно входить ускорение свободного падения g. Для периода колебаний общая зависимость будет иметь вид

,

где l-длина нити маятника.

Далее решение принимает формальный характер

или

.

Система уравнений имеет вид для L: 0=α+β; для t: 1=-2β

Решая эту систему, получим: α=1/2; β=-1/2.

Окончательный результат будет иметь вид:

(5)

Если бы начальный угол был не 16º, а другой, то зависимость (5) была бы такой же по виду, но постоянная С имела другое значение; поэтому в общем случае можно записать

,

где φ- начальный угол отклонения маятника.

Вид функции F(φ) методом анализа размерностей определить нельзя. Если эту функцию разложить в ряд Маклорена и сохранить в разложении только первый член (что можно сделать в случае малых колебаний), то получим:

где а- некоторый числовой коэффициент, значение которого методом анализа размерностей также определить невозможно (как известно из точных решений, величина а равна 2π). В последующем неизвестный постоянный коэффициент С(или а), присутствующий в виде сомножителя, возможно определить, проделав один- единственный опыт.

В данном случае достаточно взять нить длиной, около двух метров, и по найденным в опыте l и t определить значение, а с помощью зависимости (5). Если провести несколько опытов при разных значениях φ, то возможно будет определить все коэффициенты в разложении в ряд Маклорена.

З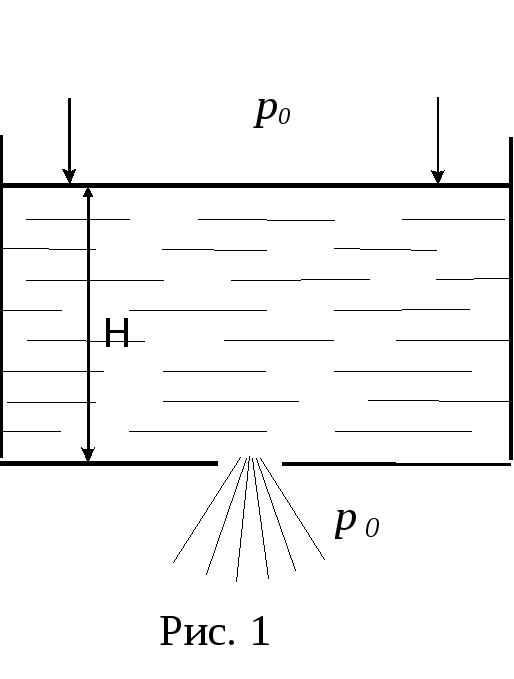амечание 6. Над размерными величинами правило размерности допускает выполнение только степенных математических операций. Все прочие операции (sin x, cos x, tg, e^x, lnx и т.д.) могут выполняться только над безразмерными величинами. Правила размерности очень полезны для проверки формул. Если вычисления проводятся в какой-то одной системе единиц, то размерности обеих частей всех полученных равенств должны быть одинаковыми. Несовпадение размерностей указывает на присутствие ошибки, допущенной при вычислениях.

Задача 3. Определить вид зависимости для скорости истечения жидкости в атмосферу через отверстие в дне открытого резервуара (рис. 1), глубина жидкости в котором равна H и поддерживается постоянной.

Решение. В процессе истечения, потенциальная энергия жидкости переходит в кинетическую энергию вытекающей струи. Переход происходит согласно соотношению:

.

Рассмотрим возможные параметры, влияющие на скорость истечения. Напор H входит в выражение для потенциальной энергии и должен обязательно присутствовать. Так как истечение происходит благодаря силе тяжести, то необходимо учитывать в качестве одного из главных параметров ускорение силы тяжести g. Рассмотрим параметры: диаметр отверстия d, форма отверстия, толщина стенки, шероховатость стенок сосуда, степень приближения отверстия к стенкам, плотность жидкости ρ, вязкость ν.

В данном случае параметров больше трех и поэтому необходимо упростить рассмотрение процесса истечения для уменьшения их. Допустим прежде всего, что жидкость идеальная и исключим тем самым вязкость из рассмотрения. Далее предположим, что отверстие круглое и диаметр его значительно меньше H, допустим также, что толщина стенки не влияет, т.е. она тонкая. Зависимость для скорости принимает вид

но по понятным причинам плотность, содержащая массу, в правую часть войти не может. Поэтому окончательно имеем

.

Применяя обычную схему решения, получаем:

или .

Для L имеем: ;

Аналогично для времени t: или , поэтому .

окончательно получаем для скорости:

. (6)

Зависимость для скорости, полученная иным способом, в действительности имеет вид:

. (7)

Если допустить, что жидкость реальная (вязкость её не равна нулю), то часть энергии переходит за счет трения в теплоту. Потенциальная энергия положения вязкой жидкости остается такой же, как и идеальной жидкости, и за счет перехода части механической энергии в теплоту, кинетическая энергия уменьшается по сравнению со случаем истечения идеальной жидкости. Если резервуар из предыдущей задачи сверху закрыт и в пространстве над жидкостью создано давление p₁, больше атмосферного, то появляется дополнительная сила, вызванная разностью давлений p=p₁-p₀ и заставляющая жидкость вытекать с большей скоростью. Для определения вида, зависимости типа ( 7), необходимо в число параметров включить p.Но в p входит масса, а в размерность левой части масса не входит, поэтому необходимо образовать параметр из p и такой величины, в которую бы входила масса, например плотности

=.

Можно предположить, что окончательный ответ в этом случае будет таким

VC.

З

Рис. 2

ависимость вида ( 7) может быть получена для самого общего случая в результате рассмотрения общих дифференциальных уравнений и, что самое главное, с учетом всех граничных условий, касающихся жидкости, формы и размеров резервуара и отверстия.

Жидкость в действительности реальная и вязкость оказывает влияние на величину скорости. Можно также заранее допустить, что на величину скорости влияет форма резервуара, близость его стенок к отверстию, толщина стенки в отверстии, форма отверстия и его величина и т.д. Все эти факторы, если их включить (даже в виде безразмерных отношений) в общую функциональную зависимость V = f (H, g) не позволили бы применить метод анализа размерностей. Нами решена здесь задача при таких (заранее не известных и определенных) условиях, когда влиянием всех факторов, кроме H и g, можно пренебречь. Навыки применения метода анализа размерностей полезны, в частности, тем, что позволяют научиться выделять главные влияющие факторы.

Задача 4. Вывести формулу для давления в пузырьке воздуха, находящегося внутри жидкости с коэффициентом поверхностного натяжения σ.

Решение. Давление внутри пузырька будет обусловлено давлением в окружающем пространстве, и кроме того, теми силами поверхностного натяжения, которые стремятся сократить поверхность, ограничивающую пузырек. К примеру, в мыльном пузыре по этой причине давление больше, чем в окружающей его среде.

В данной задаче основным параметром, влияющим на давление, будет коэффициент поверхностного натяжения σ. Кроме этого параметра, очевиден еще только один – радиус пузырька r. Тогда зависимость от давления имеет вид

p = f (σ, r)

или, в терминах первичных параметров

mL^-1t^-1 = (mt^-2)^αL^β, α=1, β=-1

и искомая зависимость примет вид

p = C.

Задача 5. Найти выражение для силы, действующей на погруженное в жидкость твердое тело и направленной вверх (закон Архимеда).

Решение. Как всегда, на начальном этапе определим все величины, влияющие на искомую величину, в данном случае на силу. Прежде всего, представим себе, что в жидкость (например, в бак с водой) погружаются тела разного объема и при этом фиксируется сила, с которой они выталкиваются жидкостью. Легко представить себе, как будут различаться выталкивающие силы, действующие на футбольный мяч и мяч для игры в настольный теннис, если их поочередно погружать в воду. В результате делаем вывод, что сила зависит от объема тела.

На следующем этапе анализа представим небольшой шар, надутый водородом, который может подниматься вверх; если его попробовать погрузить в воду, то мы встретимся с силой, которая значительно превышает ту, которая существует в воздушной среде. Делаем вывод, что искомая сила зависит также от плотности среды, в которую погружено тело. Если представить на каком-нибудь простейшем примере (например, рассмотреть параллелепипед внутри жидкости), отчего возникает сила, то получим, что основной причиной является давление, существующее внутри жидкости, оно, в свою очередь, вызвано силой земного тяготения. Поэтому в число влияющих величин необходимо включить ускорение g. Несмотря на последнее замечание, попробуем не учитывать в искомой зависимости g; тогда

где W – объем тела,

и

.

Система уравнений имеет вид

.

В данном случае одно уравнение не имеет смысла () и вместо физического объема будет входить объект размерности С другой стороны, введение в правую часть сомножителя (ускорения) делает все уравнения естественными, и поэтому заключаем, что искомая зависимость имеет вид

Тогда

,

и система уравнений имеет вид

.

Решение будет таким

.

Окончательно, искомая зависимость имеет вид

F=СWpg,

что полностью совпадает с аналитическим выражением закона Архимеда.

Задача 6. Жидкость тонкой плёнкой стекает по вертикальной стенке под действием силы тяжести. Определить вид зависимости для скорости стекания пленки.

Решение. Будем считать жидкость реальной (вязкой), не учитываем силы поверхностного натяжения, тем самым предполагая, что пленка достаточно толстая (порядка долей миллиметра) и течение происходит под действием силы тяжести, а тормозящей силой является сила трения, обусловленная вязкостью жидкости. Можно представить, как стекают по стенке пленки одной и той же жидкости, но разной толщины – поэтому может быть сделан вывод, что в число параметров должна войти толщина пленки . Причем из опыта следует, что чем толщина пленки больше, тем больше скорость стекания. Если стекают пленки двух различающихся по вязкости жидкостей, например, воды и глицерина, то скорость будет больше у пленки жидкости, чья вязкость будет меньше, т.е. пленка воды стекает быстрее, чем глицерина (при одинаковой толщине). Следовательно, в зависимость для скорости должна входить вязкость . Так как основной движущей силой является сила тяжести, то в выражение для скорости должно войти и ускорение силы тяжести g. В число параметров помимо названных не может быть включена плотность жидкости  (или она может войти вместе с одинаковыми коэффициентом вязкости в виде , чтобы исключить размерность массы в правой части).

Основываясь на приведенных рассуждениях, возможно представить соотношение для скорости в виде

.

Размерность левой части [Lt^-1], а размерность правой [t^-1], поэтому для соблюдения правила размерностей необходимо правую часть умножить на L (т.е. на ) и окончательно получаем соотношение

,

которые в данном случае выведено нами элементарно.

Решим данную задачу методом анализа размерностей. Учитывая сделанные в начале решения замечания о входящих в общее соотношение параметрах, возможно представить общий вид зависимости для скорости так

В данном случае можно заранее предполагать, что число уравнений будет меньше числа неизвестных: в размерности скорости присутствуют длина и время – т.е. будет 2 уравнения, а в правой части 3 параметра.

Применяя стандартную схему решения, получим

,

или

.

Получим в результате систему уравнений

В данном случае система неопределенная, и строго говоря, данная задача при таком подходе не может быть решена.

Решение можно получить, если ввести параметр , по своему смыслу отражающий отношение силы тяжести, действующей на стекающую пленку к силе трения. Параметр имеет размерность

Основная зависимость для скорости примет вид:

Применяя стандартную схему, получим:

.

Система уравнений будет такая:

откуда

Окончательный результат имеет вид:

В данном решении введение параметра сделало систему уравнений определенной и позволило весьма корректно применить метод анализа размерностей.

Задача 7. Методом анализа размерностей вывести зависимость для высоты подъема воды в открытой стеклянной трубке, опущенной в жидкость.

Решение. Из опытов известно, что чем меньше диаметр трубки, тем выше поднимается в ней жидкость, таким образом, одним из главных параметров в искомой зависимости является радиус трубки r. Поднятие жидкости происходит из-за сил поверхностного натяжения – поэтому коэффициент поверхностного натяжения жидкости также должен войти в зависимость. Поскольку на жидкость, кроме силы поверхностного натяжения действует сила тяжести и высота подъема зависит от веса столба жидкости, то в число аргументов необходимо добавить ускорение силы тяжести g. Предварительно, таким образом, установлен такой вид общей зависимости для высоты подъема жидкости

,

в правую часть которой входит величина , имеющая размерность и поэтому содержащая массу. Так как в левую часть масса не входит, то в аргументы правой части для исключения массы необходимо включить величину, содержащую массу; самым простым аргументом в данном случае является плотность . Такой путь рассуждений очевиден и часто применяется (особенно часто по отношению к массе).

Общая зависимость для h с учетом значения будет иметь вид

.

Применяя затем стандартную систему решения к последней зависимости, получим

Система уравнений будет иметь вид

Данная система также является неопределенной, что вынуждает искать иные приёмы решения, а именно если сформировать параметр, выражающий отношение силы поверхностного натяжения к силе тяжести, он будет иметь вид:

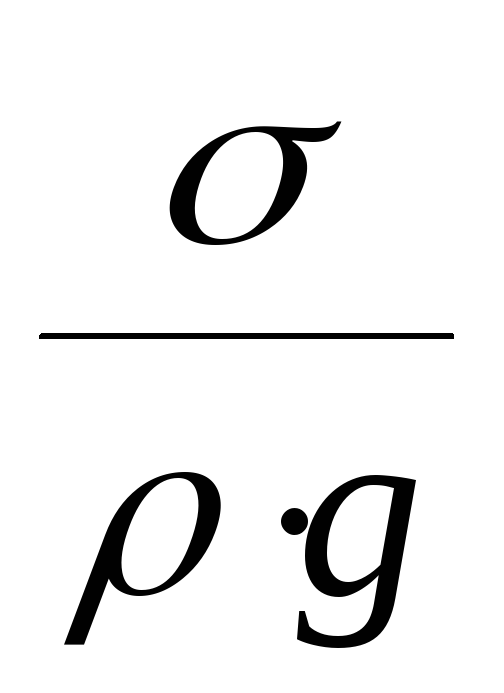
и размерность L² (безразмерный параметр в данном случае не имеет смысла – он будет просто числом и в систему уравнений не попадет). С учетом этого нового параметра зависимость для h будет иметь вид:

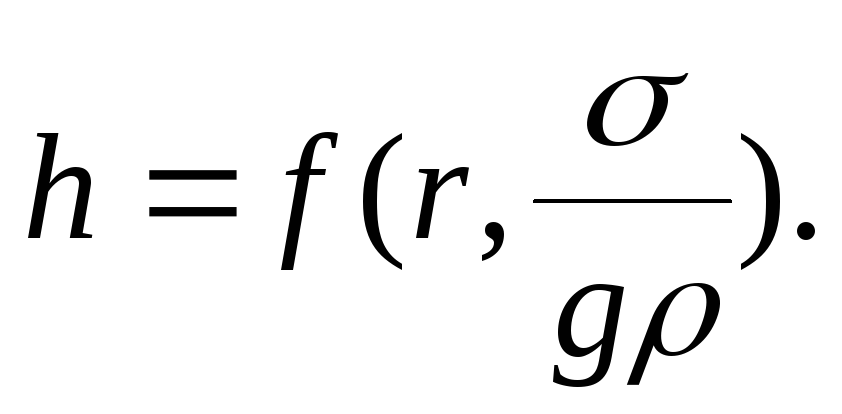
Тогда имеем:

,

откуда следует:

Принимая получим и окончательно