3. Динамические характеристики системы при изменении частоты. Лавина частоты

Изменение частоты (скорости) в переходном процессе можно определить аналитически. Предположим, что мощность, потребляемая нагрузкой, будет пропорциональна частоте:

(1)

где Р_н0 — мощность нагрузки в первый момент после возмущения; b_f — регули­рующий эффект нагрузки по частоте; — относительное изменение частоты.

В переходном режиме мощность турбины под действием регулятора турбины изменяется на величину Р_рег, которая определяется как

(2)

где T_s — постоянная времени двигателя исполнительного механизма (серводвигателя).

Дифференциальное уравнение, характеризующее изменение частоты в системе, имеет вид

(3)

где

Введем обозначения: k₁ = P_Tном/(σT_s); k.₂ — 1\T_S. Здесь σ — коэффициент неравномерности (статизм) регулятора скорости. Тогда вместо (1) запишем

Предположим, что в момент времени t — 0 изменяются мощности нагрузки. Уравнение движения записывается в операторной форме и решается. Затем находится зависимость изменения частоты от времени.

С помощью полученных выражений может быть проанализировано влияние регулирующего эффекта нагрузки.

Очевидно, что расчеты без учета регулирующего эффекта нагрузки будут давать завышенные отклонения частоты от установившегося значения. При этом надо иметь в виду, что реальные частот­ные характеристики суммарной нагрузки энергосистем могут иметь нелинейную зависимость от частоты. Однако для диапазона практически важных изменений величин ∆Р и ∆f ее с достаточной степенью точности можно считать линейной. Поэтому учет характеристик нагрузки в виде зависимости Рн = P_Ho(l + b_f∆f *) может считаться вполне приемлемым для практических расчетов изменений частоты в системах.

В установившемся режиме значение частоты

при b_f = 0 отклонение частоты

Все сказанное относится не только к агрегату, но и ко всей системе в целом, если под σ понимать σ_∑.

Эквивалентная механическая постоянная времени также зависит от режима системы или объединения. Так, в одной системе эта постоянная изменялась в тече­ние суток от 15 до 18 с зимой и от 13 до 15 с летом.

Выше предполагалось, что при набросе нагрузки турбина под действием регулятора изменяет свою мощность на Р_рег. Однако это изменение невозможно, если вся мощность турбины уже использована, т. е. полностью открыт направляющий аппарат (полный впуск пара).

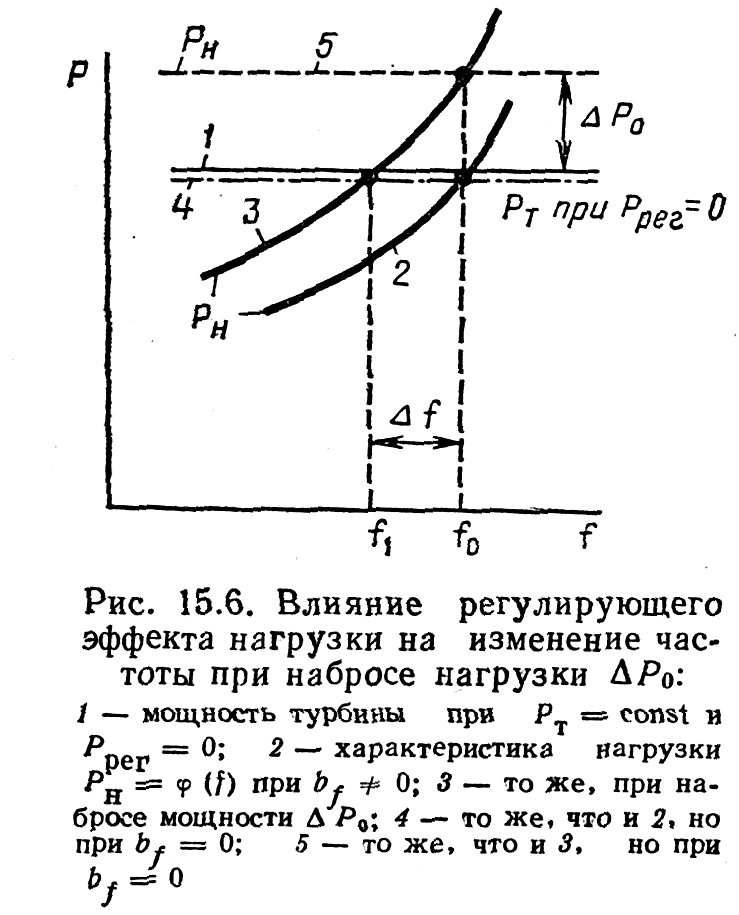
Изменение частоты ∆f* имеетэкспоненциальный характер, причем если нагрузка системы не будет зависеть от частоты (b_f == 0), то режим установиться не сможет (∆f*). Физически это означает, что при отсутствии регулирования (или саморегулирования) система не могла бы работать, так как появление малейшего небаланса ∆Р приводило бы к полному нарушению режима системы (рис. 15.6).

В зависимости от того, что понималось под T_s и σ уравнения, описывающие изменение частоты могли характеризовать изменения частоты под действием только АРС (первичный регулятор) или АРЧ (вторичный регулятор).

Нужно, однако, отметить, что постоянные времени и коэффициенты статизма, входящие в уравнения и выбираемые из условий устойчивости и конструктивных соображений, лежат в определенных пределах. Обычно встречающиеся значения этих параметров таковы, что обусловливают появление одного отрицательного действительного и двух комплексных сопряженных корней характеристического уравнения А(р) = 0. При этом решение получается в виде двух составляющих, одна из которых затухает по экспоненциальному закону с постоянной времени, примерно соответствующей постоянной времени АРЧ. На эту составляющую накладывается другая, имеющая вид затухающей синусоиды с периодом и затуханием, примерно определяющимися параметрами АРС и инерционностью агрегата. Однако такое разделение имеет место только при постоянной времени АРЧ, значительно большей постоянных T_s и Tj.

Было рассмотрено явление так называемой лавины напряжения, появляющейся при неблагоприятном сочетании характеристик, определяющих выработку генераторами реактивной мощности, с одной стороны, и потребление мощности нагрузкой — с другой.

Аналогичное явление может наблюдаться и в отношении изменений частоты. Ее небольшое начальное снижение может далее, как бы усиливаться и приобретать лавинообразный характер.

Причина этого явления заключается в снижении мощности, выдаваемой генераторами при снижении частоты. Это происходит при отсутствии резерва генерирующей мощности в системе в связи с тем, что механизмы собственных нужд тепловых станций снижают свою производительность со снижением частоты. Нарушение устойчивости может быть связано также с неправильным действием АРЧ, характеристики и параметры которых могут быть неблагоприятно выбраны в смысле устойчивости их параллельной работы. При учете влияния изменения частоты на работу генераторов характеристики мощности, генерируемой в системе, можно изобразить так, как это сделано на рис. 17.1.

Не стремясь к выявлению количественных соотношений, можно констатировать, что снижение частоты на ∆f приводит к деформации характеристики Р_Г, благодаря чему точка 0 (рис. 17.1), в которой балансируются мощности генерации и нагрузки, оказывается неустойчивой, дальнейшее снижение частоты развивается лавинообразно и приводит к полному нарушению устойчивости системы.

Приведенные на рис. 17.1 характеристики строились в предположении постоянства напряжения (величина которого, например, поддерживается регулируемым синхронным компенсатором). В действительности одновременно со снижением частоты будет происходить и уменьшение напряжение. Уменьшение скорости вращения генераторов будет приводить к снижению их э. д. с.. Реактивная мощность у генераторов будет уменьшаться, а у нагрузки — увеличиваться.

Рис. 17.1. Развитие лавины частоты: 1 2 — характеристика генератора при действия АРС—АРЧ; 2 3 — характеристика генератора при полном открытии (естественная); 2 3' — характеристика генератора при полном открытии и снижении мощности с уменьшением частоты из-за влияния собственного расхода вспомогательного оборудова­ния станции; 2 3"— то же, что и 2 3', но при более резком влиянии вспомогательного оборудования; Рн1, Рн0 — характеристика мощности и мощность нагрузки в нормальном режиме; Рн2, Рн20, Рн3, Рн30 Рн4 Рн40 –то же, что при набросах нагрузки. 1',1",2 — точки устойчивого режима; А, В — точки критического режима, приводящего к лавине частоты; 0 — точка неустойчивого режима

Хотя в условиях сниженной частоты критическое напряжение (при котором наступает опрокидывание двигателей) уменьшается, все же при значительном снижении частоты могут создаваться условия для возникновения и развития лавины напряжения.

МЕРЫ ПРЕДОТВРАЩЕНИЯ НЕУСТОЙЧИВОСТИ (ЛАВИНЫ) ЧАСТОТЫ. АВТОМАТИЧЕСКАЯ РАЗГРУЗКА ПО ЧАСТОТЕ

Из приведенного анализа можно сделать следующие выводы. Снижение частоты в электрической системе в некоторых случаях приводит к уменьшению активной мощности, выдаваемой генераторами, что может привести к неустойчивости их режима (лавине частоты).

Понижение частоты вызывает уменьшение выдачи реактивной мощности и в то же время увеличение потребления реактивной мощности нагрузкой, что приводит к понижению напряжения в узлах нагрузки системы. При снижении частоты до 43—45 Гц напряжение может снизиться до критического значения, при котором возникает лавина напряжения. Лавина частоты и лавина напряжения вызывают массовое отключение потребителей от действия защиты и нарушение параллельной работы электрических станций. Ликвидация таких аварий и восстановление нормального режима системы могут длиться несколько часов.

Явления лавины частоты и лавины напряжения протекают в течение нескольких десятков секунд или даже секунд. В такое короткое время правильная оценка создавшегося положения и проведение необходимых мероприятий со стороны дежурного персонала в системе весьма затруднительны. Понижение частоты до опасных пределов практически может быть предотвращено в двух случаях: а) если в системе имеется достаточно большой вращающийся резерв; б) если с понижением частоты автоматически отключается некоторая часть нагрузки, т. е. производится так называемая автоматическая частотная разгрузка (АЧР).

Наиболее быстро дополнительную мощность можно получить, если вращающийся резерв составляют гидрогенераторы, однако инерционность регулирования гидротурбин позволяет выдать агрегатам резерва всю их мощность только через 15—20 с. Это не всегда может предотвратить аварию. Эффективность гидрогенераторного резерва значительно повышается при уменьшении времени регулирования путем выдергивания иглы катаракта, что практически, однако, не всегда используется. Резерв на тепловых электрических станциях может быть эффективен только при достаточной мощности котлов и оборудования агрегатов совершенными автоматическими устройствами. Запуск резервных агрегатов при понижении частоты во многих случаях не может предотвратить развития аварии, так как даже гидрогенераторам требуется несколько минут (не менее 1—2) для набора мощности. Эффективными в этом отношении могут быть резервные агрегаты со специальными газовыми или авиационными турбинами (обычно устанавливаются отработавшие свой срок на самолетах двигатели). Однако установка таких специальных агрегатов пока не получила широкого распространения. Суммарная мощность обычного вращающегося резерва, выбранного по условиям экономичности, как правило, составляет 10—20%, а часто оказывается и меньше. В часы максимума нагрузки системы вращающийся резерв может полностью отсутствовать. Однако при авариях, связанных с отключением генераторов и станции или с разделением системы на отдельные части, дефицит мощности может достигать 30% и более. Поэтому в такого рода аварийных условиях наиболее надежным решением является автоматическое отключение соответствующей части нагрузки. Эту задачу и выполняют устройства автоматической разгрузки по частоте (АЧР).

Роль АЧР особенно велика в энергетических системах небольшой и средней мощности с малым числом электрических станций и слабо развитыми электрическими сетями. По мере укрупнения энергетических систем относительная (а не абсолютная) величина возможного аварийного небаланса мощности снижается. Однако даже в мощных объединенных энергосистемах отказываться от АЧР было бы нецелесообразно. Так, если при объединении систем уменьшается вероятность глубокого понижения частоты во всей объединенной системе, то остается опасность возникновения подобных аварий при отделении каких-либо ее частей или более мелких систем, а также при разделении объединенной системы как несинхронно работающие части. Таким образом, в объединенных системах большое значение имеет местная разгрузка по частоте.

Литература: [1], § 9.10

[7], § 15.1-15.4