3. Анализ Статической устойчивости нерегулируемой электрической системы

Переходные процессы без учета электромагнитных процессов в контурах ротора, с упрощенным учетом демпферного момента будут описыватьсяодним нелинейным дифференциальным уравнением второго порядка

или в операторной форме

где Р_т = Р₀ = Р_мsinδ – мощность турбины, определяющая исходный режим; Рэл = Р_мsinδ – электромагнитная мощность синхронного генератора, являющаяся нелинейной функцией.

Разложим Р_мsinδ в ряд Тейлора по величине ∆δ в окрестности δ₀ , оставляя только нулевой и линейный члены разложения. Получим

Обозначим С₁ =, получим линеаризованное по первому приближению дифференциальное уравнение

Уравнение имеет решение

Характеристическое уравнение

имеет два корня

где- собственная частота колебаний ротора синхронной машины;- декркмент затухания.

Анализ устойчивости.

При с₁ >0 система всегда будет устойчива.

При оба корня будут действительные отрицательные и процесс будет проходить по затухающей экспоненте.

При оба корня будут комплексными с отрицательными вещественными частями и процесс будет колебательный с затухающей амплитудой..

При с₁ < 0 система всегда будет неустойчива апериодически.

При с₁ = 0 появляется один нулевой корень и один корень, равный . Наличие нулевого корня указывает на критический случай и нужно провести дополнительное исследование.

При наличии значительного активного сопротивления в цепи статора эквивалентный демпферный момент может изменить знак и стать моментом дополнительно ускоряющим генератор, приводящим к самораскачиванию. Аналогичный эффект могут дать регуляторы скорости или возбуждения при неправильной настойке.

Анализ Статической устойчивости нерегулируемой электрической системы с учетом электромагнитных переходных процессов в обмотке возбуждения. САмовозбуждение.

Переходные процессы в простой нерегулируемой системе описываются системой нелинейных дифференциальных уравнений

где Т_d0 – постоянная времени обмотки возбуждения синхронной машины; - вынужденная составляющая ЭДС синхронной машины, обусловленная действием АРВ.

Электромагнитная мощность генератора Рэл является функцией 2-х переменных - и δ, а также переходной ЭДС=φ(, δ)

При линеаризации уравнения (1) по первому приближению по двум переменным и δ, в ряду Тейлора появляются три члена:

Уравнение (1) запишем в операторной форме

где

Взаимосвязь между ,, δ определяется уравнением

Из (4) найдем Id

Подставим Idв (3) получим

Линеаризуем (2) по первому приближению

Система линеаризованных уравнений

Так как , то

или

Запишем главный определитель

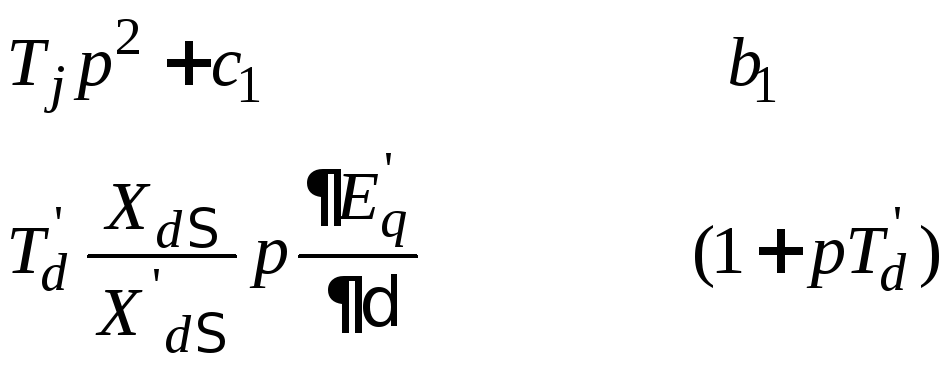
Приращения всех переменных выразим через приращения

Главный определитель системы

+

+

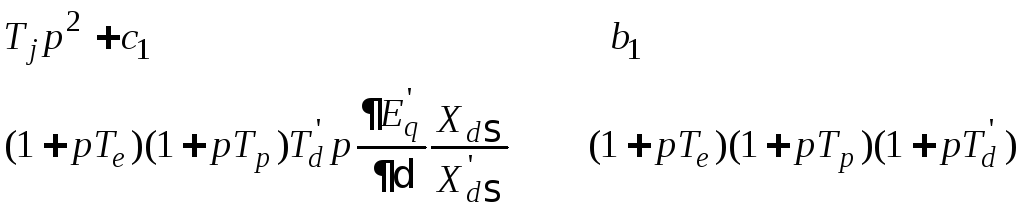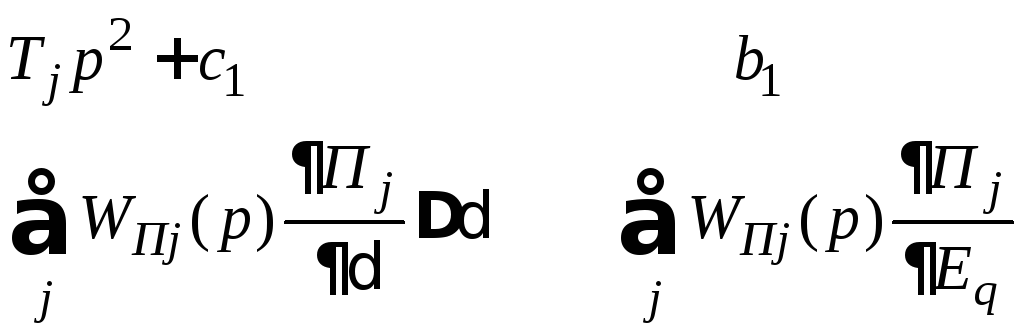
Запишем D(p) в виде суммы двух многочленов

D(p) = D₀(p) + D₁(p)

где D₀(p) =;

D₁(p) =

В многочлен D₀(p) передаточная функция АРВ не входит; влияние АРВ отражает многочлен D₁(p).

- единичные добавки или множители при коэффиицентах регулирования, зависят от параметров регулирования и режима.

Все коэффициенты усиления АРВ в выражении принимаются положительными. Отклонеия всех параметров определяются как

Отклонения напряжения .

Анализ устойчивости может проводится с помощью различных критериев, которые классифицируются как алгебраические: методы Гурвица и Раусса и частотные- методы D-разбиения, Михайлова, Найквиста.

Критерий Гурвица устанавливает соотношения между коэффициентами характеристичексого уравнения в виде неравенств, соблюдение которых является необходимым и достаточным условием статической устойчивости системы.

При АРВ пропорционального действия коэффициенты многочленов имеют следующие аналитичексие выражения

где

Анализ устойчивочти.

Необходимым условием устойчивости является положительность всех коэффициентов характеристического уравнения.

Если > 0, то а₀ и а₁ всегда больше нуля.

Условие а₃ > 0 cводится к требованию или при отрицательном с₁ – к требованию, т.е. величина с₂ должна быть больше нуля.

Условие при с₂ > 0 и требованию всегда соблюдается.

Условие сводится к требованию установления коэффициента усиления, большего некоторого минимально допустимого значения т.е..

Приравняв главный определитель Гурвица нулю получим величину максимально допустимого коэффициента усиления по отклонению напряжения