
- •Раздел 3. Динамика
- •Глава 14. Введение в динамику.
- •14.2 Законы механики Галилея – Ньютона.
- •15. Дифференциальные уравнения движения материальной точки. Принцип Даламбера для материальной точки. Две основные задачи динамики точки.
- •15.2. Дифференциальные уравнения движения материальной точки в проекциях на оси естественного трехгранника.
- •15.3. Принцип Даламбера для материальной точки
- •15.4. Две основные задачи материально точки
- •15.5. Интегрирование дифференциальных уравнений движения материальной точки
- •16. Общие теоремы динамики точки
- •16.1. Количество движения и кинетическая энергия точки. Импульс силы.
- •16.2. Теорема об изменении количества движения точки.
- •16.3. Момент количества движения точки относительно центра и оси. Теорема об изменении момента количества движения точки (теорема моментов)
- •16.4. Работа силы. Мощность
- •16.5. Примеры вычисления работы.
- •16.6. Теорема об изменении кинетической энергии точки
- •17. Свободные прямолинейные колебания материальной точки
- •17.1. Свободные горизонтальные колебания точки
- •17.2. Свободные вертикальные колебания груза
- •18. Относительное движение материальной точки
- •18.1. Дифференциальные уравнения движения материальной точки в неинерциальной системе отсчета.
- •18.2. Частные случаи относительно движения точки
- •19. Момент инерции.
- •19.1. Момент инерции твердого тела. Радиус инерции.
- •19.2. Момент инерции твердого тела относительно параллельных осей (теорема Гюйгенса)
- •19.3. Момент инерции простейших твердых тел и плоских фигур
- •19.4. Центробежные моменты инерции. Понятие о главных осях инерции тела
- •20. Общие теоремы динамики системы
- •20.1 Вводные определения и дифференциальные уравнения движения
- •20.2 Теоремы об изменении количества движения и теорема о движении центра масс
- •20.3 Теорема об изменении кинетического момента
- •20.4 Теорема об изменении кинетической энергии
- •21. Приложение теорем динамики системы к динамике твердого тела
- •21.1. Дифференциальные уравнения поступательного движения твердого тела
- •21.2. Определение динамических реакций подшипников при вращении твердого тела вокруг неподвижной оси
- •21.3 Дифференциальные уравнения плоскопараллельного (плоского) движения твердого тела
- •21.4 Элементарная теория гироскопа
- •21.5 Дифференциальные уравнения движения твердого тела вокруг неподвижной точки (сферического движения)
- •22. Начала аналитической механики
- •22.1 Введение
- •22.2 Принцип возможных перемещений
- •22.3 Принцип Даламбера. Общее уравнение динамики
- •22.4 Уравнения Лагранжа второго рода
- •22.5 Принцип Гамильтона – Остроградского
- •22.6 Обобщенное уравнение энергии
- •23. Малые колебания консервативной системы около положения равновесия
- •23.1 Кинетическая и потенциальная энергия малых колебаний
- •23.2 Понятие об устойчивости равновесия
- •23.3 Малые свободные колебания системы с одной степенью свободы
- •23.4 Малые свободные колебания системы с двумя степенями свободы
- •24. Теория удара
- •24.1 Исходные предположения и основной закон
- •24.2 Упругий и неупругий удары. Коэффициент восстановления
- •24.3 Общие теоремы при ударе
17.2. Свободные вертикальные колебания груза
Рассмотрим теперь колебания груза М массы mна вертикальной пружине жесткости с. Примем груз за материальную точку.
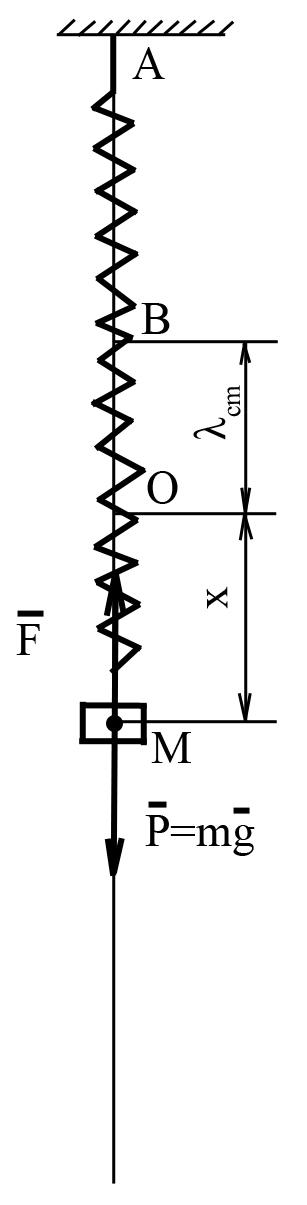
Рис. 13
Пусть ABна рис. 13 означает
недеформированную пружину, закрепленную
в точке А. После подвешивания груза и
медленного (статического) опускания
конец пружины займет равновесное
положение О, которое и примем за начало
координат, направив ось![]() вертикально вниз. Отрезок ВО называется
статическим удлинением
вертикально вниз. Отрезок ВО называется
статическим удлинением![]() пружины. Поскольку в положение равновесия
сила упругости пружины равна весу груза
пружины. Поскольку в положение равновесия
сила упругости пружины равна весу груза![]() ,
то по формуле (4.2)
,
то по формуле (4.2)![]() .
Откуда
.
Откуда
|
|
(4.7) |
Рассмотрим положение груза М и а некоторый
момент колебаний. На груз М действует
сила тяжести
![]() и упругая сила пружины
и упругая сила пружины![]() ,
так как удлинение пружины
,
так как удлинение пружины![]() .
.
Дифференциальное уравнение запишется в виде:
![]()
После деления на mполучим![]()
![]() ,
т.е то же самое дифференциальное уравнение
(4.3), что и для горизонтальных колебаний.
Поскольку в силу (4.7)
,
т.е то же самое дифференциальное уравнение
(4.3), что и для горизонтальных колебаний.
Поскольку в силу (4.7)![]() ,
то период колебаний можно записать в
виде
,
то период колебаний можно записать в
виде
![]()
18. Относительное движение материальной точки
Дифференциальные уравнения движения материальной точки в неинерциальной системе отсчета.
Частные случаи относительно движения точки.
18.1. Дифференциальные уравнения движения материальной точки в неинерциальной системе отсчета.
Второй закон динамики и полученные из него ранее уравнения и теоремы верны только для абсолютного движения точки, т.е. движения по отношению к инерциальной системе отсчета.
Пусть точка М массы mдвижется под действием сил![]() .
Рассмотрим движение этой точки
относительно системы координат
.
Рассмотрим движение этой точки
относительно системы координат![]() ,
которая в свою очередь каким – то
известным нам образом движется
относительно инерциальной системы
координат
,
которая в свою очередь каким – то
известным нам образом движется
относительно инерциальной системы
координат![]() (рис.14).
(рис.14).
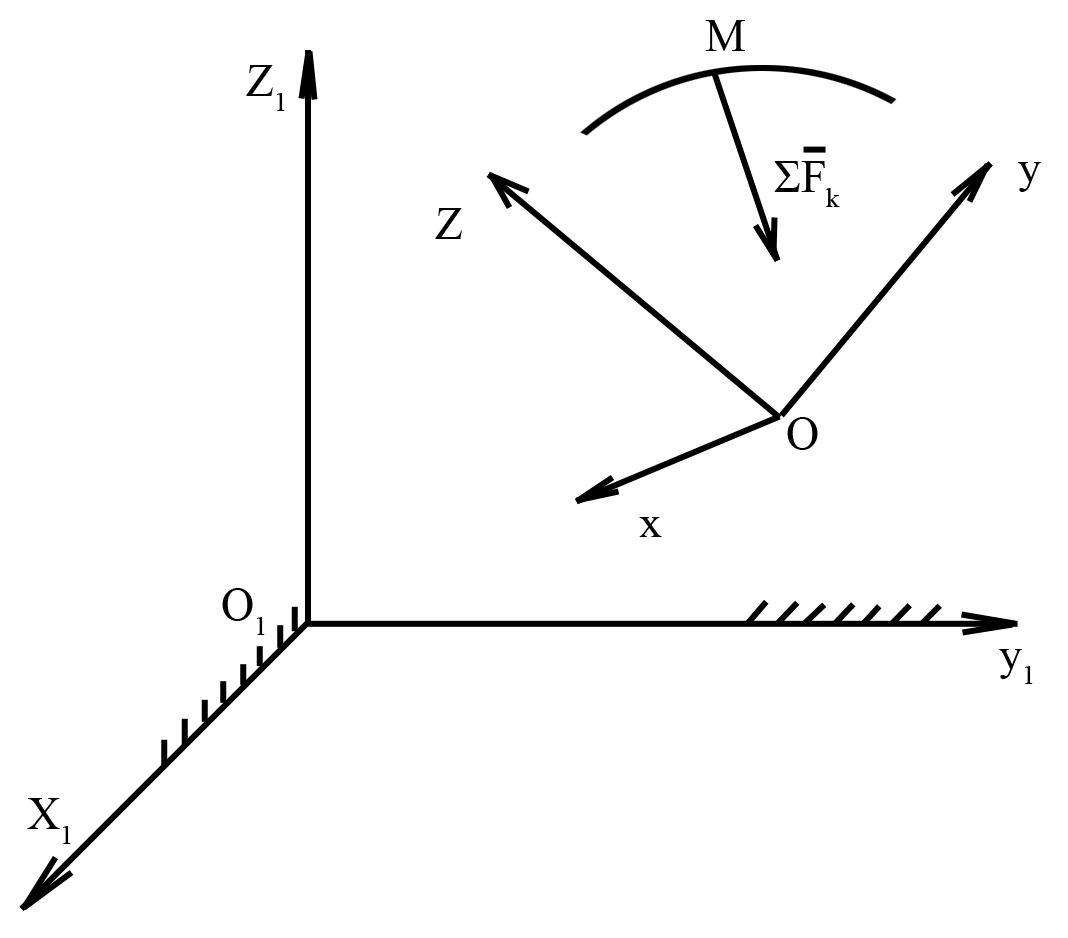
Рис. 14
Найдем зависимость между относительным
ускорением точки
![]() и действующими на нее силами. Для
абсолютного движения основной закон
динамики имеет вид:
и действующими на нее силами. Для
абсолютного движения основной закон
динамики имеет вид:
|
|
(5.1) |
Из кинематики известно, что абсолютное
ускорение
![]() ,
где
,
где
![]() ,
,![]() ,
,![]() –
относительное, переносное и кориолисово
ускорения точки.
–
относительное, переносное и кориолисово
ускорения точки.
Подставляя
![]() в равенство (5.1) и считая в дальнейшем
в равенство (5.1) и считая в дальнейшем![]() ,
так как эта величина представляет собой
ускорение изучаемого нами относительного
движения, получим
,
так как эта величина представляет собой
ускорение изучаемого нами относительного
движения, получим![]() .
Так как
.
Так как![]() - переносная сила инерции;
- переносная сила инерции;![]() - кориолисова сила инерции, то
- кориолисова сила инерции, то
|
|
(5.2) |
Равенство (5.2) выражает основной закон динамики для относительного движения точки. Сравнивая равенства (5.1) и (5.2) приходим к выводу: все уравнения и теоремы механики составляются так же, как уравнения абсолютного движения, если при этом к действующим на точку силам присоединить переносную и кориолисову силы инерции.
Проецируя равенство (5.2) на оси подвижной
системы координат
![]() получим дифференциальные уравнения
движения точки в неинерциальной системе
отсчета:
получим дифференциальные уравнения
движения точки в неинерциальной системе
отсчета:
![]()
![]()
18.2. Частные случаи относительно движения точки
Если подвижные оси движутся поступательно, то
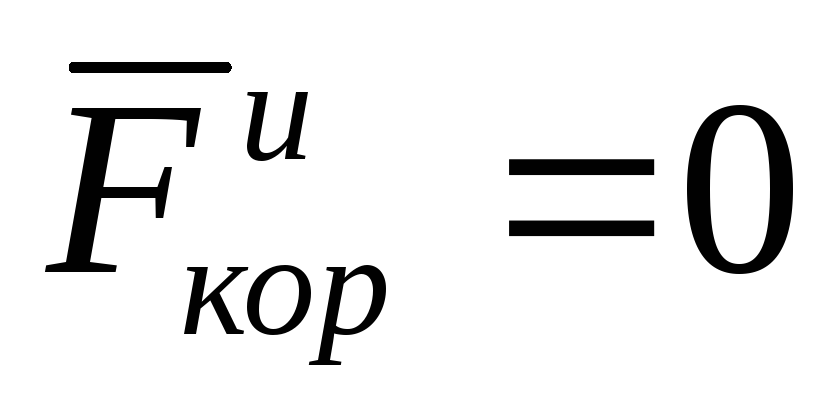 ,
так как в этом случае
,
так как в этом случае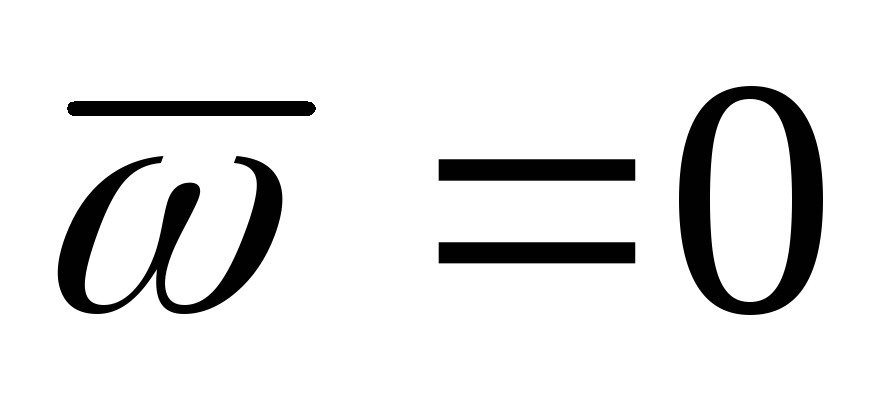 (
( -
угловая скорость вращения подвижных
осей
-
угловая скорость вращения подвижных
осей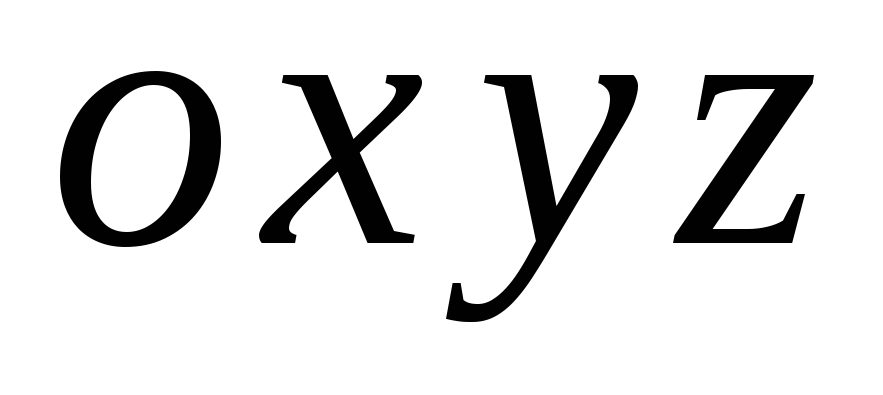 )
и закон относительного движения
принимает вид:
)
и закон относительного движения
принимает вид:
![]()
Если подвижные оси перемещаются поступательно, равномерно и прямолинейно, то
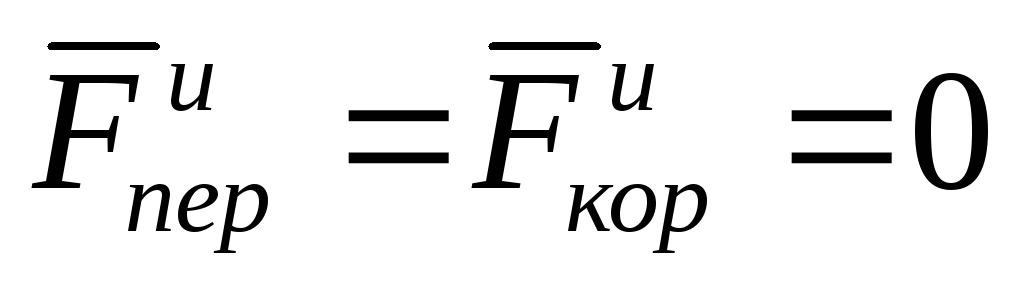 и закон относительного движения
принимает вид
и закон относительного движения
принимает вид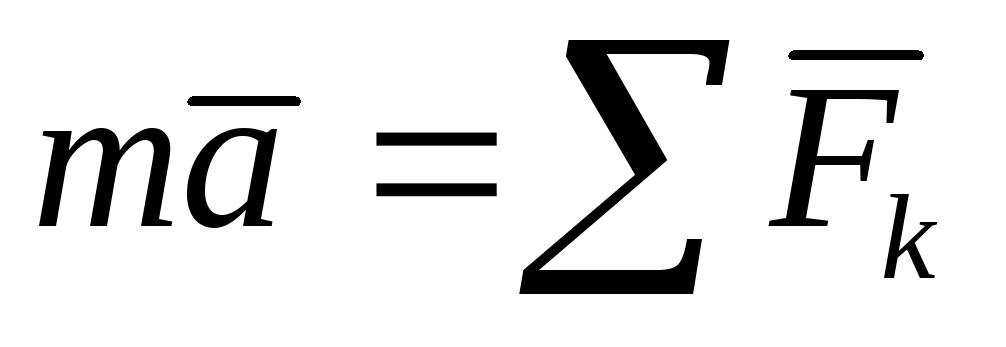 ,
т.е. такой же вид, как и закон относительного
движения, принимает вид, как и закон
движения по отношению к неподвижным
осям. Следовательно, такая система
отсчета также будет инерциальной.
,
т.е. такой же вид, как и закон относительного
движения, принимает вид, как и закон
движения по отношению к неподвижным
осям. Следовательно, такая система
отсчета также будет инерциальной.
Из полученного результата вытекает, что никаким механическим экспериментом нельзя обнаружить, находится ли данная система отсчета в покое или совершает поступательное, равномерное и прямолинейное движение. В этом состоит открытый еще Галилеем принцип относительности классической механики.
Если точка по отношению к подвижным осям находится в покое, то для нее
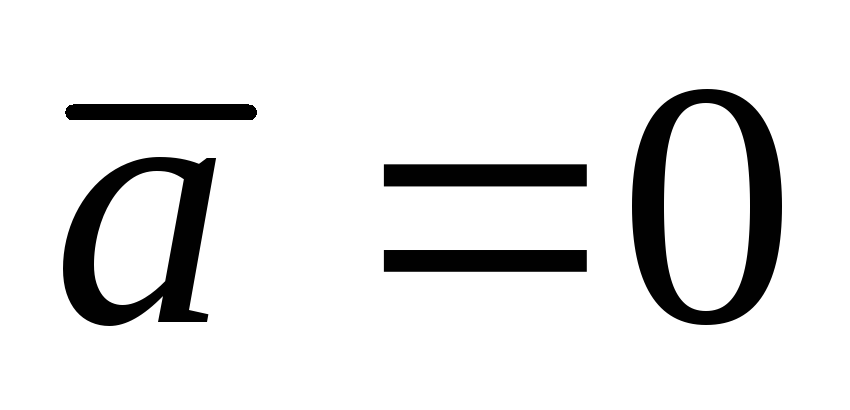 и
и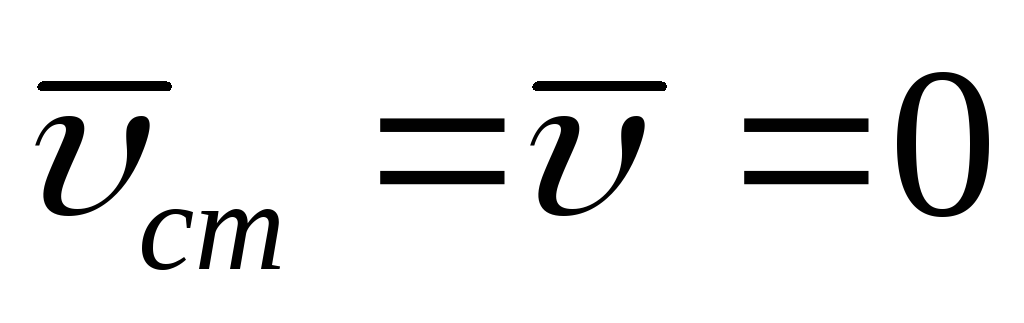 ,
а следовательно и
,
а следовательно и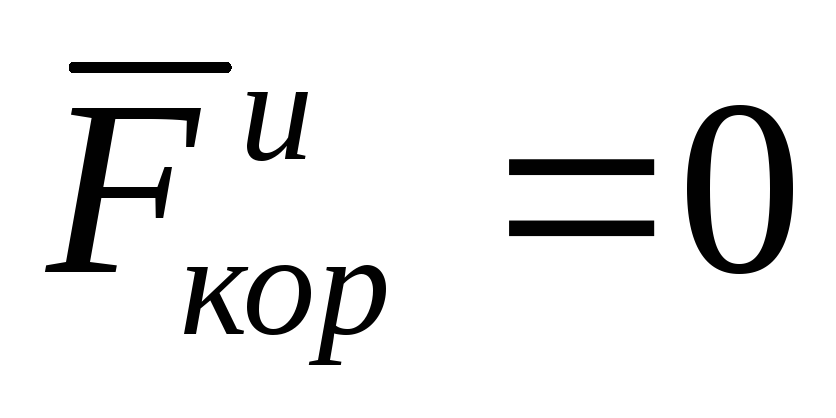 ,
так как кориолисово ускорение
,
так как кориолисово ускорение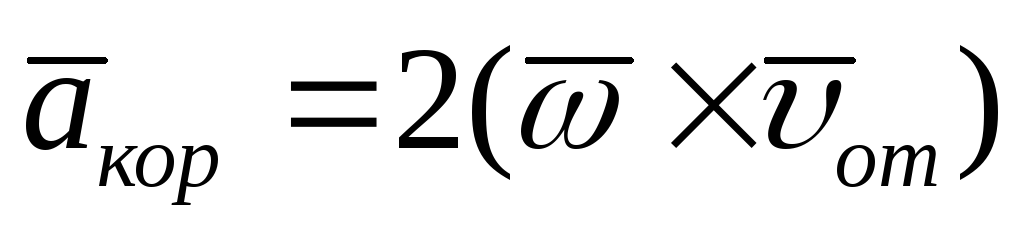 .
Тогда равенство (5.2) примет вид
.
Тогда равенство (5.2) примет вид
|
|
(5.3) |
Уравнение (5.3) представляет собой уравнение относительного равновесия (покоя) точки.
