16.6. Теорема об изменении кинетической энергии точки

Пусть точка массы mдвижется под действием сил. Запишем для данной точки основное уравнение динамики (2) (1.2)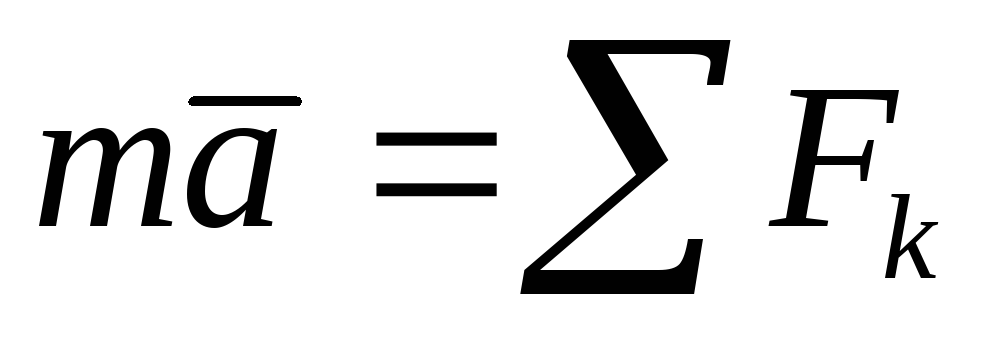

Проецируя его на касательную , получим.

Касательное ускорение представим в виде 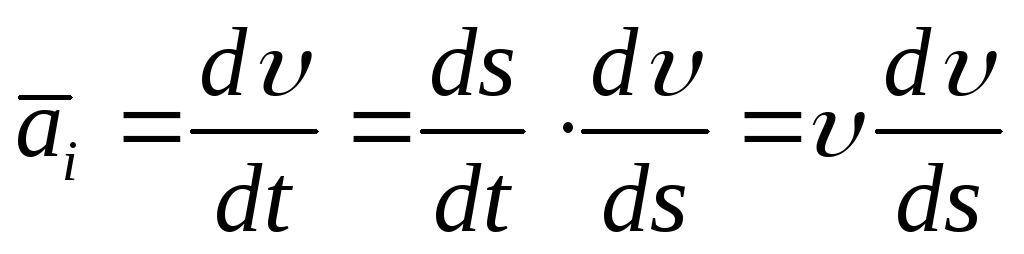, тогда

Умножим обе части этого равенства на и внесемпод знак дифференциала. Тогда замечая, что, где– элементарная работа силы, получим

(3.11)

Равенство (3.11) выражает теорему об изменении кинетической энергии точки в дифференциальной форме. Если в начальном положении скорость точки равна , а в конечном -, то интегрируя равенство (3.11), получим:

(3.12)

Равенство (3.12) выражает теорему об изменении кинетической энергии точки в конечной форме: изменение кинетической энергии точки на некотором ее конечном перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.

Теорема об изменении кинетической энергии точки применяется, в основном, на тех же участках траектории движения точки, где задан путь пройденной точкой или этот путь надо определить.

17. Свободные прямолинейные колебания материальной точки

17.1 Свободные горизонтальные колебания точки.

17.2 Свободные вертикальные колебания груза.

17.1. Свободные горизонтальные колебания точки

Рассмотрим прямолинейное горизонтальное движение точки М массы mпо неподвижной гладкой плоскости под действием упругой силы (рис. 12)пружины.

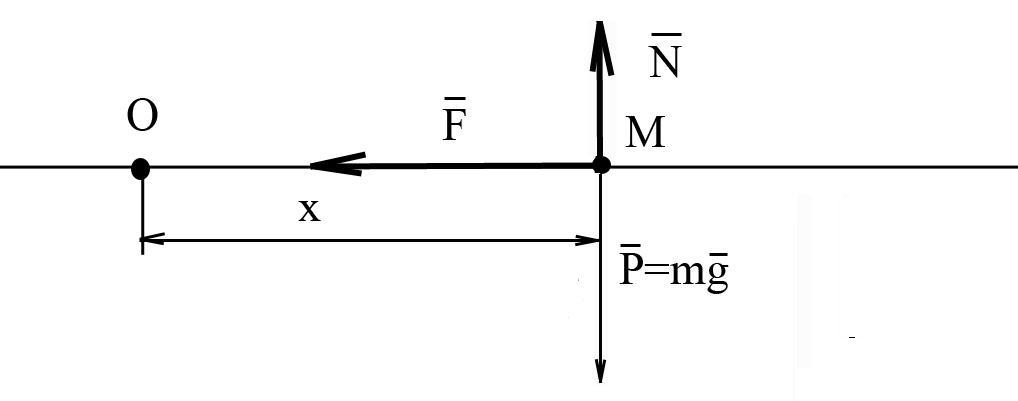
Рис. 12

Начало координат О выберем в положении равновесия точки и направим ось вправо по оси пружины. Пусть М – одно из положений точки в ее движении, возникшем в результате нарушения состояния равновесия. На точку М действуют три силы: сила тяжести, сила реакциигладкой плоскости и упругая сила пружины. Пусть упругая сила подчиняется закону Гука, т.е ее алгебраическое значениепропорционально величине деформации (растяжения или сжатия) пружины

(4.1)

Знак минус означает, что при растяжении пружины (x> 0) имеем< 0, т.е упругая сила направлена в отрицательную сторону оси; при сжатии - наоборот. Коэффициент пропорциональности, размерность которого н/м, называется жесткостью (упругостью) пружины. Из формулы (4.1) имеем:

(4.2)

Составим дифференциальное уравнение движения точки М в проекции на ось :или.

Обозначая , получим:

(4.3)

Уравнение (4.3) представляет собой дифференциальное уравнение свободных колебаний материальной точки по гладкой горизонтальной плоскости.

Уравнение (4.3) является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Полагая в уравнении , получим для определенияnхарактеристическое уравнение. Поскольку корни этого уравнения являются чисто мнимыми, то как известно из теории дифференциальных уравнений, общее решение уравнения (4.3) имеет вид

,

(4.4)

где и- постоянные интегрирования. Если вместо постоянныхиввести постоянныеитакие, что,, то получимили.

Это другой вид решения уравнения (4.3), в котором постоянными интегрирования являются и.

Колебания, совершаемые точкой по закону (4.5), называются гармоническими колебаниями. Скорость точки

(4.6)

Величина , равная небольшому отклонению точки М от точки О, называется амплитудой колебаний. Величинаназывается фазой колебаний. Фаза, в отличие от координатыопределяет не только положение точки в данный момент времени, но и направление ее последующего движения, например из положения М при фазе равной, точка движения вправо, а при фазе, равной, влево. Фазы, отличающиеся на, считаются одинаковыми. Величинаопределяет фазу начала колебаний (начальная фаза). Например приколебания происходят по закону синуса (начинаются от центра О со скоростью, направленной вправо), при- по закону косинуса (начинаются из положениясо скоростью). Величинаназывается круговой частотой колебаний.

Промежуток времени ( или), в течении которого точка совершает одно полное колебание, называется периодом колебаний. По истечению периода фаза изменяется на, откуда период.

Найдем значения и.

Пусть в момент времени точка М находится в положениии имеет скорость. Подставляя эти значения в (4.5) и (4.6), получим,. Отсюда складывая вначале почленно квадраты этих равенств, а затем деля их почленно одно на другое, найдем,.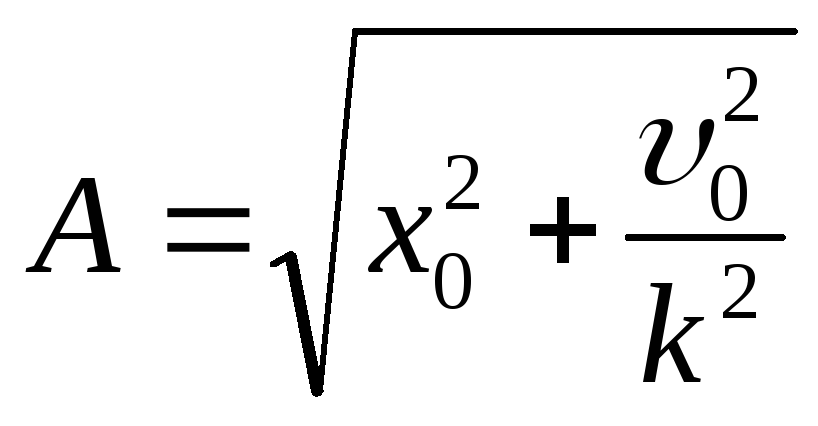

Отметим важные свойства свободных колебаний:

1. амплитуда и начальная фаза колебаний зависят от начальных условий;

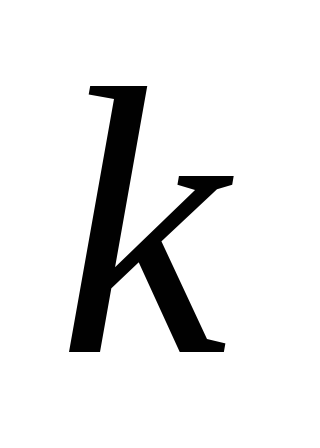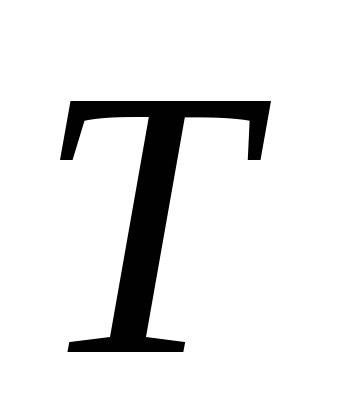2. частота , а следовательно и периодколебаний от начальных условий не зависят.