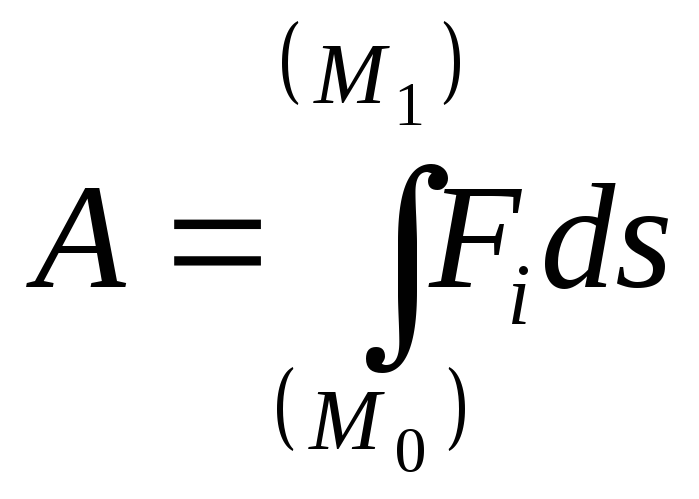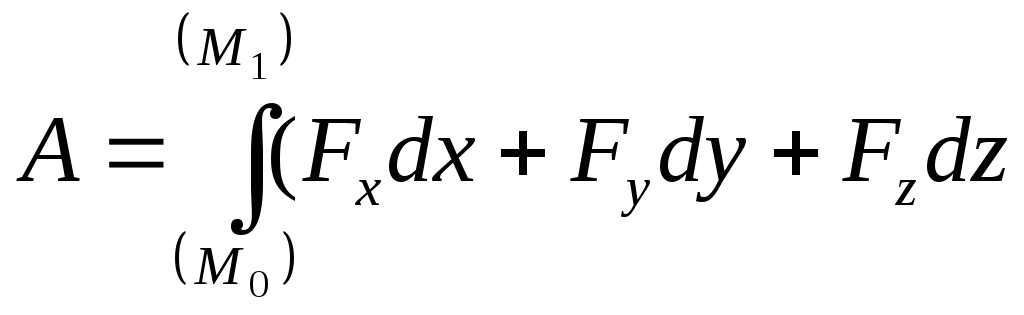- •Раздел 3. Динамика
- •Глава 14. Введение в динамику.
- •14.2 Законы механики Галилея – Ньютона.
- •15. Дифференциальные уравнения движения материальной точки. Принцип Даламбера для материальной точки. Две основные задачи динамики точки.
- •15.2. Дифференциальные уравнения движения материальной точки в проекциях на оси естественного трехгранника.
- •15.3. Принцип Даламбера для материальной точки
- •15.4. Две основные задачи материально точки
- •15.5. Интегрирование дифференциальных уравнений движения материальной точки
- •16. Общие теоремы динамики точки
- •16.1. Количество движения и кинетическая энергия точки. Импульс силы.
- •16.2. Теорема об изменении количества движения точки.
- •16.3. Момент количества движения точки относительно центра и оси. Теорема об изменении момента количества движения точки (теорема моментов)
- •16.4. Работа силы. Мощность
- •16.5. Примеры вычисления работы.
- •16.6. Теорема об изменении кинетической энергии точки
- •17. Свободные прямолинейные колебания материальной точки
- •17.1. Свободные горизонтальные колебания точки
- •17.2. Свободные вертикальные колебания груза
- •18. Относительное движение материальной точки
- •18.1. Дифференциальные уравнения движения материальной точки в неинерциальной системе отсчета.
- •18.2. Частные случаи относительно движения точки
- •19. Момент инерции.
- •19.1. Момент инерции твердого тела. Радиус инерции.
- •19.2. Момент инерции твердого тела относительно параллельных осей (теорема Гюйгенса)
- •19.3. Момент инерции простейших твердых тел и плоских фигур
- •19.4. Центробежные моменты инерции. Понятие о главных осях инерции тела
- •20. Общие теоремы динамики системы
- •20.1 Вводные определения и дифференциальные уравнения движения
- •20.2 Теоремы об изменении количества движения и теорема о движении центра масс
- •20.3 Теорема об изменении кинетического момента
- •20.4 Теорема об изменении кинетической энергии
- •21. Приложение теорем динамики системы к динамике твердого тела
- •21.1. Дифференциальные уравнения поступательного движения твердого тела
- •21.2. Определение динамических реакций подшипников при вращении твердого тела вокруг неподвижной оси
- •21.3 Дифференциальные уравнения плоскопараллельного (плоского) движения твердого тела
- •21.4 Элементарная теория гироскопа
- •21.5 Дифференциальные уравнения движения твердого тела вокруг неподвижной точки (сферического движения)
- •22. Начала аналитической механики
- •22.1 Введение
- •22.2 Принцип возможных перемещений
- •22.3 Принцип Даламбера. Общее уравнение динамики
- •22.4 Уравнения Лагранжа второго рода
- •22.5 Принцип Гамильтона – Остроградского
- •22.6 Обобщенное уравнение энергии
- •23. Малые колебания консервативной системы около положения равновесия
- •23.1 Кинетическая и потенциальная энергия малых колебаний
- •23.2 Понятие об устойчивости равновесия
- •23.3 Малые свободные колебания системы с одной степенью свободы
- •23.4 Малые свободные колебания системы с двумя степенями свободы
- •24. Теория удара
- •24.1 Исходные предположения и основной закон
- •24.2 Упругий и неупругий удары. Коэффициент восстановления
- •24.3 Общие теоремы при ударе
16.4. Работа силы. Мощность
Элементарной работой силы
![]() на элементарном перемещении
на элементарном перемещении![]() называется
скалярная величина
называется
скалярная величина![]() (рис. 6)
(рис. 6)
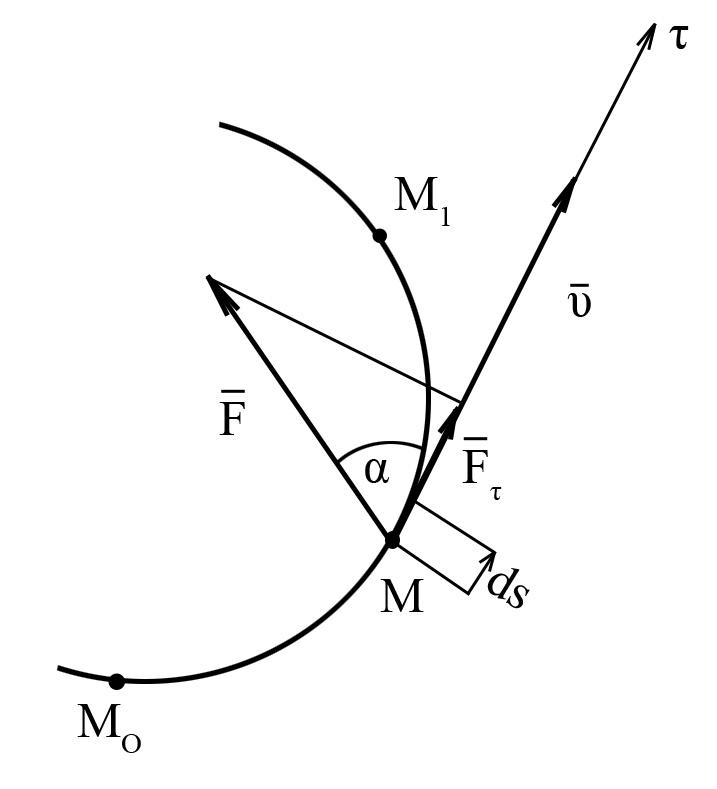
Рис. 6
Так как
![]() ,
то
,
то
(3.6)
![]()
![]() ,
если сила
,
если сила![]() способствует движению точки
способствует движению точки![]() - острый.
- острый.
![]() ,
если сила
,
если сила![]() препятствует движению точки
препятствует движению точки![]() - тупой.
- тупой.
![]() ,
если
,
если![]()
Если учесть, что
![]() ,
где
,
где![]() - вектор элементарного перемещения
точки М и воспользоваться известным из
векторной алгебры понятием о скалярном
произведении двух векторов, то равенство
(3.6) можно записать в виде
- вектор элементарного перемещения
точки М и воспользоваться известным из
векторной алгебры понятием о скалярном
произведении двух векторов, то равенство
(3.6) можно записать в виде
|
|
(3.7) |
Следовательно, элементарная работа
силы равна скалярному произведению
силы на вектор элементарного перемещения
ее точки приложения. Через проекции
векторов
![]() и
и![]() на
координатные оси равенство (37) запишется
в виде
на
координатные оси равенство (37) запишется
в виде![]() –
аналитическое выражение элементарной
работы.
–
аналитическое выражение элементарной
работы.
Работа силы на любом конечном перемещении
![]() будет равна
будет равна
|
|
(3.8) |
или
|
|
(3.9) |
Если
![]() ,
то
,
то![]() ,
где
,
где![]() .
.
Мощность. Мощностью называется величина,
определяющая работу, совершаемую силой
в единицу времени. Если работа совершается
равномерно, то мощность
![]() ,
где
,
где![]() – время, в течении которого совершена
работа А
– время, в течении которого совершена
работа А
В общем случае
![]()
16.5. Примеры вычисления работы.
1. Работа силы тяжести.
Пусть точка М, на которую действует сила
тяжести
![]() ,
переместилась из положения
,
переместилась из положения![]() в положение
в положение![]() (рис.7)
(рис.7)
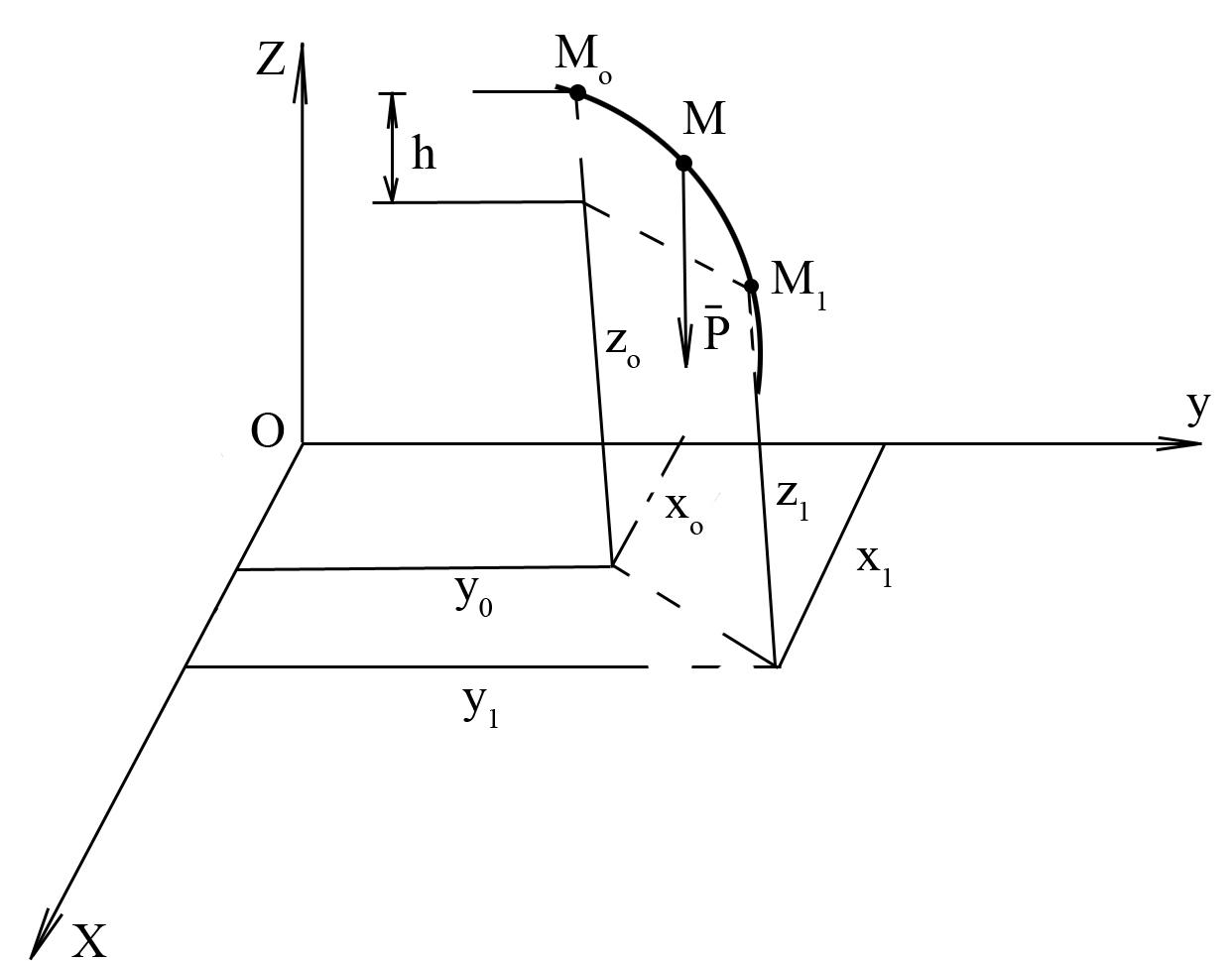
Рис. 7
Тогда
![]() ,
,![]() .
Подставляя эти значения в формулу (3.9),
получим
.
Подставляя эти значения в формулу (3.9),
получим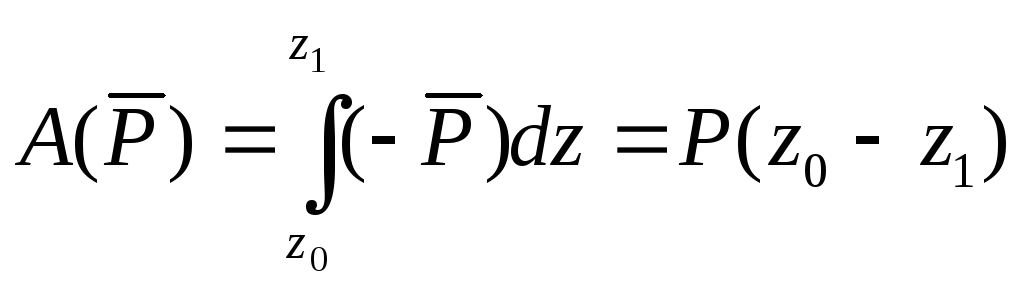
обозначая
![]() ,
получим
,
получим
|
|
(3.10) |
Если точка
![]() выше (ниже) точки
выше (ниже) точки![]() ,
то
,
то![]() ,
(
,
(![]() )
)
Из равенства (3.10) видно, что работа силы тяжести не зависит от траектории движения точки М, а зависит только от ее вертикального перемещения h.
2. Работа силы упругости.
Пусть длина ненапряженной пружины
![]() .
Растянем (сожмем) пружину до длины
.
Растянем (сожмем) пружину до длины![]() .
Тогда по закону Гука возникает сила
упругости
.
Тогда по закону Гука возникает сила
упругости![]() .
по модулю
.
по модулю![]() ,
где с н/м – коэффициент упругости
(жесткости) пружины,
,
где с н/м – коэффициент упругости
(жесткости) пружины,![]() - деформация пружины.
- деформация пружины.

Рис. 8
Примем конец О ненапряженной пружины
за начало координат (рис.8). Тогда
![]() и
и![]() .
У нас
.
У нас![]() .
По формуле (3.9), имеем
.
По формуле (3.9), имеем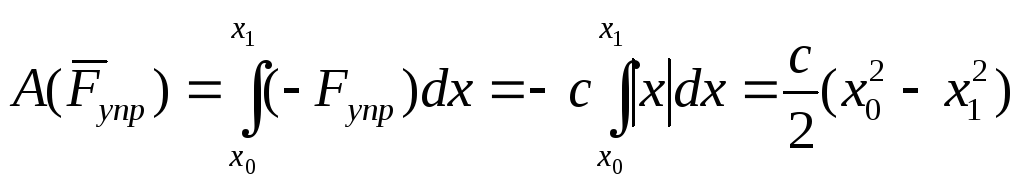 .
.
Так как
![]() – начальная деформация пружины, где
– начальная деформация пружины, где![]() – начальная длина пружины.
– начальная длина пружины.
![]() – конечная деформация пружины, то, где
– конечная деформация пружины, то, где![]() – конечная длина пружины, то
– конечная длина пружины, то
![]()
3. Работа силы трения скольжения.
Пусть точка движется по некоторой шероховатой поверхности (рис. 9).
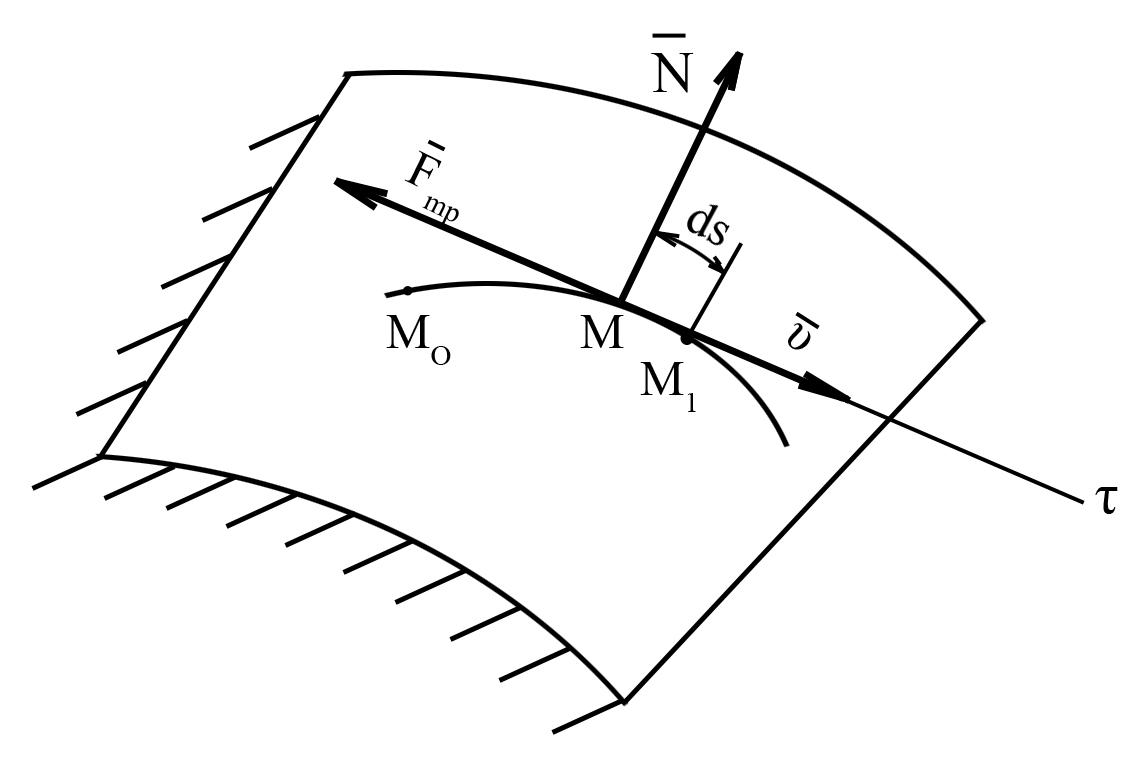
Рис. 9
Тогда на точку будет действовать сила
трения скольжения
![]() .
По модулю
.
По модулю![]() ,
где
,
где![]() - коэффициент трения скольжения,N– нормальная реакция поверхности. Так
как сила
- коэффициент трения скольжения,N– нормальная реакция поверхности. Так
как сила![]() препятствует движению точки, то ее
элементарная работа
препятствует движению точки, то ее
элементарная работа![]()
Полная работа
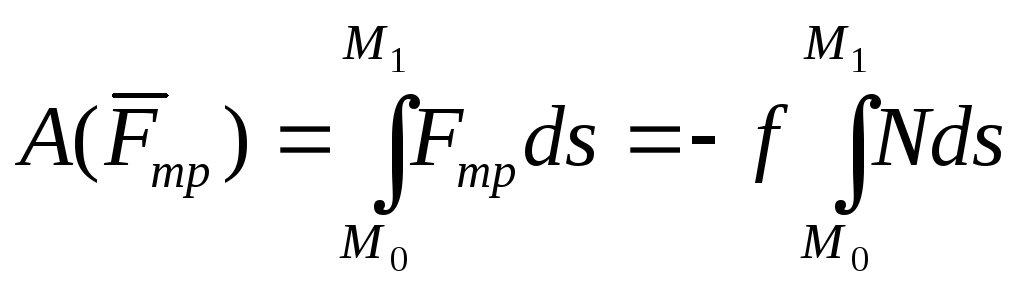 .
Если
.
Если![]() ,
то
,
то![]() ,
где
,
где![]() =
=![]()
![]()
4. Работа силы, приложенной к вращающемуся телу (работа момента).
Пусть к твердому телу, которое может
вращаться вокруг неподвижной оси Zв точке М, приложена сила![]() (рис.10).
Элементарная работа этой силы будет
равна
(рис.10).
Элементарная работа этой силы будет
равна![]() .
Так как
.
Так как![]() - момент силы
- момент силы![]() относительно осиZ, то
относительно осиZ, то![]() ,
где
,
где![]() - элементарный угол поворота тела вокруг
осиZ. Такая работа при
повороте тела на угол
- элементарный угол поворота тела вокруг
осиZ. Такая работа при
повороте тела на угол![]() ,
будет равна
,
будет равна![]() .
.
Если
![]() ,
то
,
то![]() .
.
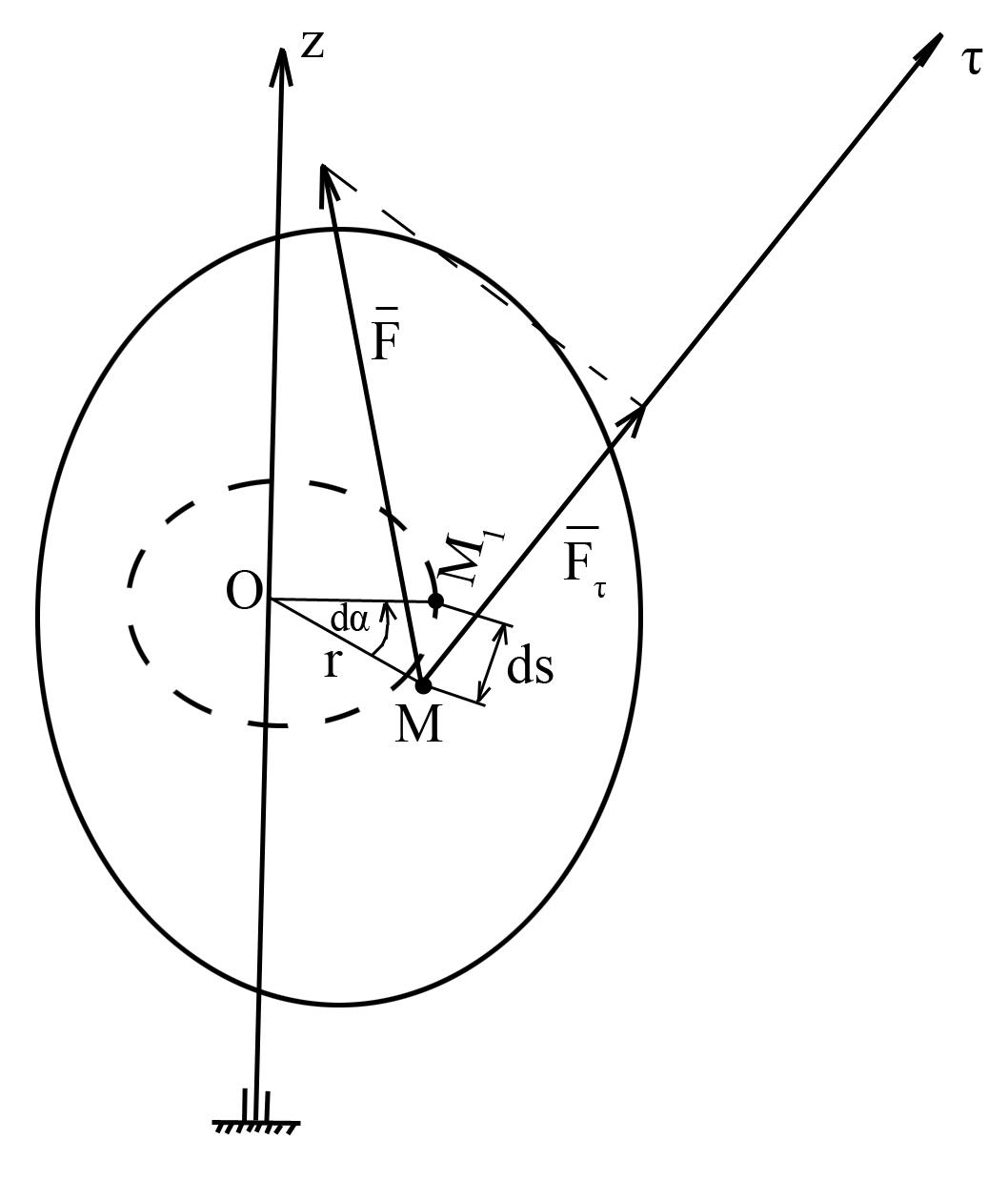
Рис. 10
Работа момента положительна (отрицательна), если момент способствует (препятствует) вращению тела вокруг оси Z.
5. Работа сил трения качения.
Как было показано в статике, сопротивление
качению создает возникающая, вследствие
деформации поверхностей тел, пара с
моментом
![]() ,
где
,
где![]() -
коэффициент трения качения;N-
нормальная реакция.
-
коэффициент трения качения;N-
нормальная реакция.
Так как момент
![]() препятствует качению тела, то его
элементарная работа
препятствует качению тела, то его
элементарная работа![]() , где
, где![]() - элементарный угол поворота тела вокруг
мгновенного центра скоростейB.
(рис. 11).
- элементарный угол поворота тела вокруг
мгновенного центра скоростейB.
(рис. 11).
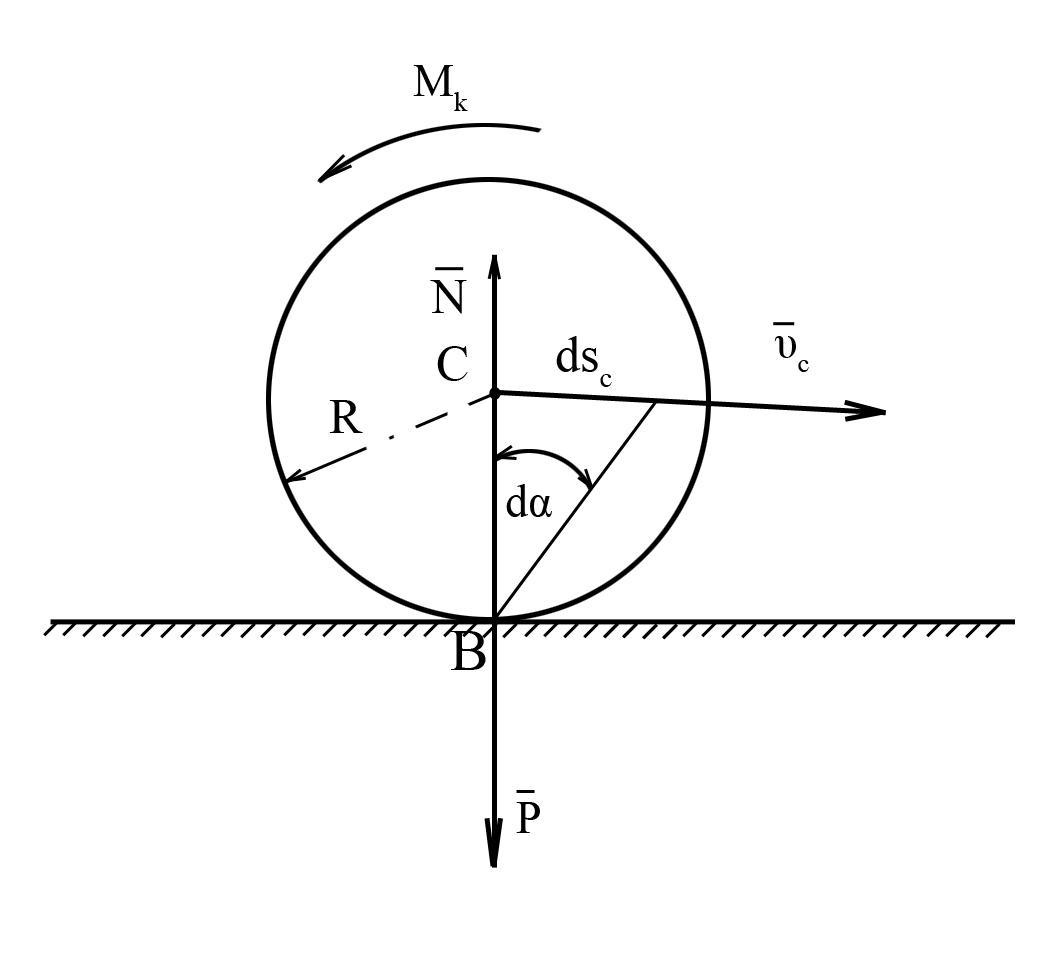
Рис. 11
Учитывая, что
![]() ,
где
,
где![]() – радиус, получим
– радиус, получим![]()
При
![]()
![]() , где
, где![]() - путь, пройденный центром
- путь, пройденный центром![]() .
.